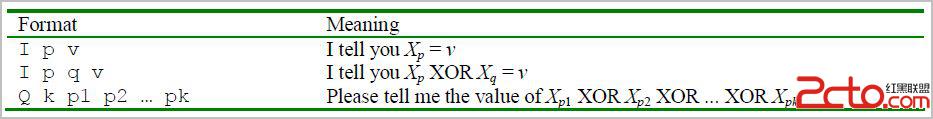程式師世界 >> 編程語言 >> C語言 >> C++ >> 關於C++ >> HDU3234&&UVA12232&&LA4487:Exclusive

HDU3234&&UVA12232&&LA4487:Exclusive

編輯：關於C++

Problem Description You are not given n non-negative integers X₀, X₁, ..., X_n-1 less than 2²⁰ , but they do exist, and their values never change.

I'll gradually provide you some facts about them, and ask you some questions.

There are two kinds of facts, plus one kind of question:

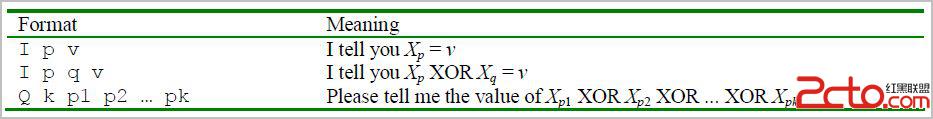
Input There will be at most 10 test cases. Each case begins with two integers n and Q (1 <= n <= 20,000, 2 <= Q <= 40,000). Each of the following lines contains either a fact or a question, formatted as stated above. The k parameter in the questions will be a positive integer not greater than 15, and the v parameter in the facts will be a non-negative integer less than 2²⁰. The last case is followed by n=Q=0, which should not be processed.
Output For each test case, print the case number on its own line, then the answers, one on each one. If you can't deduce the answer for a particular question, from the facts I provide you before that question, print "I don't know.", without quotes. If the i-th fact (don't count questions) cannot be consistent with all the facts before that, print "The first i facts are conflicting.", then keep silence for everything after that (including facts and questions). Print a blank line after the output of each test case.

Sample Input

Sample Output

Case 1:
I don't know.
3
1
2
Case 2:
4
Case 3:
7
The first 2 facts are conflicting.

Source 2009 Asia Wuhan Regional Contest Hosted by Wuhan University

題意：對於n個數a[0]~a[n-1]，但你不知道它們的值，通過逐步提供給你的信息，你的任務是根據這些信息回答問題
I P V ：告訴你a[P] = V I P Q V：告訴你a[P] XOR a[Q] = V Q K P1..PK：詢問a[P1]^a[P2]^...a[PK]的值
思路：很經典的並查集題目 r[a]記錄的是a與其父親節點的異或值通過並查集合並的過程同時更新路徑上的r值令fa,fb分別是a,b,的父親節點我們知道r[a] = a^fa,r[b]=b^fa,a^b=c 那麼在合並fa,fb的時候，令fb為fa的父節點那麼就有r[fa]=fa^fb 而r[a]=a^fa,所以fa=a^r[a] 同理fb=b^r[b] 所以r[fa] = r[a]^r[b]^a^b = r[a]^r[b]^c 當然對於一個節點合並問題不好解決，此時可以添加一一個新節點n作為根節點，使得n的值為0，那麼任何值與0的異或都是本身這樣一來合並問題就解決了
然後對於查詢而言，對於n是根節點的我們不需要考慮，但是對於不是以n為跟節點的，根節點的值被重復計算了，這個時候我們要統計根節點被統計的次數，如果是奇數次，那麼必然是無法確定的了

#include 
#include 
#include 
#include 
#include 
#include 
#include
#include 
#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

#define lson 2*i
#define rson 2*i+1
#define LS l,mid,lson
#define RS mid+1,r,rson
#define UP(i,x,y) for(i=x;i<=y;i++)
#define DOWN(i,x,y) for(i=x;i>=y;i--)
#define MEM(a,x) memset(a,x,sizeof(a))
#define W(a) while(a)
#define gcd(a,b) __gcd(a,b)
#define LL long long
#define N 20005
#define INF 0x3f3f3f3f
#define EXP 1e-8
#define lowbit(x) (x&-x)
const int mod = 1e9+7;

int n,m,tot;
int father[N],r[N],num[N],u,v,w,vis[N];
char str[100];

int find(int x)
{
    if(x!=father[x])
    {
        int fx = father[x];
        father[x] = find(father[x]);
        r[x]^=r[fx];
    }
    return father[x];
}

bool Union(int a,int b,int c)
{
    int fa = find(a),fb=find(b);
    if(fa==fb)
    {
        if((r[a]^r[b])!=c) return false;
        return true;
    }
    if(fa==n) swap(fa,fb);
    father[fa] = fb;
    r[fa] = r[a]^r[b]^c;
    return true;
}

int query()
{
    int i,j,cnt,ans = 0;
    MEM(vis,0);
    for(i = 0; i