You are given string s. Your task is to determine if the given string s contains two non-overlapping substrings AB and BA (the substrings can go in any order).
InputThe only line of input contains a string s of length between 1 and 105 consisting of uppercase Latin letters.
OutputPrint YES (without the quotes), if string s contains two non-overlapping substrings AB and BA, and NO otherwise.
Sample test(s) InputABAOutput
NOInput
BACFABOutput
YESInput
AXBYBXAOutput
NONote
In the first sample test, despite the fact that there are substrings AB and BA, their occurrences overlap, so the answer is NO.
In the second sample test there are the following occurrences of the substrings: BACFAB.
In the third sample test there is no substring AB nor substring BA.
題目大意:給一個字符串,問能否找到兩個不相互覆蓋的子串AB和BA
題目分析:暴力掃4次,第一二次先掃AB後掃BA,第三四次先掃BA後掃AB,注意這組樣例ABACCCAB
#include#include #include using namespace std; int const MAX = 1e5 + 5; char s1[MAX], s2[MAX]; int main() { scanf(%s, s1); memcpy(s2, s1, sizeof(s1)); int len = strlen(s1); bool f1 = false; bool f2 = false; for(int i = 0; i < len; i++) { if(s1[i] == 'A' && s1[i + 1] == 'B') { f1 = true; s1[i] = s1[i + 1] = '*'; break; } } for(int i = 0; i < len; i++) if(s1[i] == 'B' && s1[i + 1] == 'A') f2 = true; if(f1 && f2) { printf(YES ); return 0; } f1 = f2 = false; for(int i = 0; i < len; i++) { if(s2[i] == 'B' && s2[i + 1] == 'A') { f1 = true; s2[i] = s2[i + 1] = '*'; break; } } for(int i = 0; i < len; i++) if(s2[i] == 'A' && s2[i + 1] == 'B') f2 = true; if(f1 && f2) { printf(YES ); return 0; } printf(NO ); }
B. Preparing Olympiad time limit per test 2 seconds memory limit per test 256 megabytes
You have n problems. You have estimated the difficulty of the i-th one as integer ci. Now you want to prepare a problemset for a contest, using some of the problems you've made.
A problemset for the contest must consist of at least two problems. You think that the total difficulty of the problems of the contest must be at least l and at most r. Also, you think that the difference between difficulties of the easiest and the hardest of the chosen problems must be at least x.
Find the number of ways to choose a problemset for the contest.
InputThe first line contains four integers n, l, r, x (1 ≤ n ≤ 15, 1 ≤ l ≤ r ≤ 109, 1 ≤ x ≤ 106) — the number of problems you have, the minimum and maximum value of total difficulty of the problemset and the minimum difference in difficulty between the hardest problem in the pack and the easiest one, respectively.
The second line contains n integers c1, c2, ..., cn (1 ≤ ci ≤ 106) — the difficulty of each problem.
OutputPrint the number of ways to choose a suitable problemset for the contest.
Sample test(s) Input3 5 6 1 1 2 3Output
2Input
4 40 50 10 10 20 30 25Output
2Input
5 25 35 10 10 10 20 10 20Output
6Note
In the first example two sets are suitable, one consisting of the second and third problem, another one consisting of all three problems.
In the second example, two sets of problems are suitable — the set of problems with difficulties 10 and 30 as well as the set of problems with difficulties 20 and 30.
In the third example any set consisting of one problem of difficulty 10 and one problem of difficulty 20 is suitable.
題目大意:有n個問題每個難度為ci,要選一些題出來,要求這些題的總難度不超過r且不小於l,且難度最大的和難度最小的差不能小於x,問有多少種選法
題目分析:n等於15,隨便搞,我是直接深搜,簡潔明了
#include#include #include using namespace std; int const INF = 0x3fffffff; int n, l, r, x; int c[20]; int ans; void DFS(int idx, int ma, int mi, int sum) //第幾個題,當前最大,當前最小,難度總和 { if(idx == n + 1) return; if(sum <= r && sum >= l && x <= ma - mi && idx == n) ans ++; DFS(idx + 1, max(ma, c[idx]), min(mi, c[idx]), sum + c[idx]); //選第idx個 DFS(idx + 1, ma, mi, sum); //不選第idx個 return; } int main() { scanf(%d %d %d %d, &n, &l, &r, &x); for(int i = 0; i < n; i++) scanf(%d, &c[i]); ans = 0; DFS(0, 0, INF, 0); printf(%d , ans); }
You are given a non-negative integer n, its decimal representation consists of at most 100 digits and doesn't contain leading zeroes.
Your task is to determine if it is possible in this case to remove some of the digits (possibly not remove any digit at all) so that the result contains at least one digit, forms a non-negative integer, doesn't have leading zeroes and is divisible by 8. After the removing, it is forbidden to rearrange the digits.
If a solution exists, you should print it.
InputThe single line of the input contains a non-negative integer n. The representation of number n doesn't contain any leading zeroes and its length doesn't exceed 100 digits.
OutputPrint NO (without quotes), if there is no such way to remove some digits from number n.
Otherwise, print YES in the first line and the resulting number after removing digits from number n in the second line. The printed number must be divisible by 8.
If there are multiple possible answers, you may print any of them.
Sample test(s) Input3454Output
YES 344Input
10Output
YES 0Input
111111Output
NO
題目大意:給個數字,問刪去其中一些數字後能不能被8整除
題目分析:打了個小表,找了找規律,首先有8或0的直接可以,其次包含16,24,32,56,64,72,96之一的都可以,再其次,先找一個奇數,它後面為12,36,44,52,76,92之一的都可以,數字長度很小,暴搞
#include#include int const MAX = 105; char s[MAX]; int len; // 0 // 8 // 16 // 24 // 32 // 56 // 64 // 72 // 96 // 112 // 136 // 144 // 152 // 176 // 192 // 312 // 336 bool judge1(int i, char ch1, char ch2) { if(s[i] == ch1) { for(int j = i + 1; j < len; j++) { if(s[j] == ch2) { printf(YES %c%c , ch1, ch2); return true; } } } return false; } bool judge2(char ch, int i, char ch1, char ch2) { for(int j = i + 1; j < len; j++) { if(s[j] == ch1) { for(int k = j + 1; k < len; k ++) { if(s[k] == ch2) { printf(YES %c%c%c , ch, ch1, ch2); return true; } } } } return false; } int main() { scanf(%s, s); len = strlen(s); for(int i = 0; i < len; i++) { if(s[i] == '0') { printf(YES 0 ); return 0; } if(s[i] == '8') { printf(YES 8 ); return 0; } if(judge1(i, '1', '6')) return 0; if(judge1(i, '2', '4')) return 0; if(judge1(i, '3', '2')) return 0; if(judge1(i, '5', '6')) return 0; if(judge1(i, '6', '4')) return 0; if(judge1(i, '7', '2')) return 0; if(judge1(i, '9', '6')) return 0; if((s[i] - '0') % 2 == 1 && judge2(s[i], i, '1', '2')) return 0; if((s[i] - '0') % 2 == 1 && judge2(s[i], i, '3', '6')) return 0; if((s[i] - '0') % 2 == 1 && judge2(s[i], i, '4', '4')) return 0; if((s[i] - '0') % 2 == 1 && judge2(s[i], i, '5', '2')) return 0; if((s[i] - '0') % 2 == 1 && judge2(s[i], i, '7', '6')) return 0; if((s[i] - '0') % 2 == 1 && judge2(s[i], i, '9', '2')) return 0; } printf(NO ); }
E. Brackets in Implications time limit per test:2 seconds memory limit per test:256 megabytes
Implication is a function of two logical arguments, its value is false if and only if the value of the first argument is true and the value of the second argument is false.
Implication is written by using character ' ', and the arguments and the result of the implication are written as '0' (false) and '1' (true). According to the definition of the implication:
', and the arguments and the result of the implication are written as '0' (false) and '1' (true). According to the definition of the implication:




When a logical expression contains multiple implications, then when there are no brackets, it will be calculated from left to fight. For example,
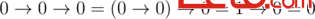 .
.
When there are brackets, we first calculate the expression in brackets. For example,
 .
.
For the given logical expression  determine if it is possible to place there brackets so that the value of a logical expression is false. If it is possible, your task is to find such an arrangement of brackets.
determine if it is possible to place there brackets so that the value of a logical expression is false. If it is possible, your task is to find such an arrangement of brackets.
The first line contains integer n (1 ≤ n ≤ 100 000) — the number of arguments in a logical expression.
The second line contains n numbers a1, a2, ..., an ( ), which means the values of arguments in the expression in the order they occur.
), which means the values of arguments in the expression in the order they occur.
Print NO (without the quotes), if it is impossible to place brackets in the expression so that its value was equal to 0.
Otherwise, print YES in the first line and the logical expression with the required arrangement of brackets in the second line.
The expression should only contain characters '0', '1', '-' (character with ASCII code 45), '>' (character with ASCII code 62), '(' and ')'. Characters '-' and '>' can occur in an expression only paired like that: (->) and represent implication. The total number of logical arguments (i.e. digits '0' and '1') in the expression must be equal to n. The order in which the digits follow in the expression from left to right must coincide with a1, a2, ..., an.
The expression should be correct. More formally, a correct expression is determined as follows:
Expressions 0, 1 (without the quotes) are correct. If v1, v2 are correct, then v1->v2 is a correct expression. If v is a correct expression, then (v) is a correct expression.The total number of characters in the resulting expression mustn't exceed 106.
If there are multiple possible answers, you are allowed to print any of them.
Sample test(s) Input4 0 1 1 0Output
YES (((0)->1)->(1->0))Input
2 1 1Output
NOInput
1 0Output
YES 0
題目大意:給四個轉移式子,然後給一個0/1串問是否存在某總計算方式使得最後答案為0,存在則輸出任意一種合法的方式
題目分析:從給的四個式子中可以發現如果結果要為0,最後一位必須是0,現在要做的就是再最後一個0之前構造1,我們可以發現如果最後一個0的前面一個是1,那麼不管這個1之前是什麼最後答案都是1,因為0 ->1=1,1 ->1=1,即與前面的值無關,所以我們轉過來考慮不可能的情況,考慮最後一個0的前面是0,因為要構1,又0->0=0,1->0=0也就是說這個0前面不能是1,依次類推可以得到,如果倒數第二個0的前面都是1,那必然無解,否則就有解
#include#include int const MAX = 1e6 + 5; int n, a[MAX]; int main() { scanf(%d, &n); for(int i = 1; i <= n; i++) scanf(%d, &a[i]); if(n == 1) //特判一個數 { if(a[1] == 1) printf(NO ); else printf(YES 0 ); return 0; } if(a[n] == 1) { printf(NO ); return 0; } bool flag = false; for(int i = 1; i <= n - 2; i++) { if(a[i] != 1) { flag = true; break; } } if(!flag && a[n - 1] == 0 && a[n] == 0) //1111111 1 0Y 0 0N { printf(NO ); return 0; } printf(YES ); for(int i = 1; i <= n - 2; i++) printf((%d->, a[i]); printf(%d, a[n - 1]); for(int i = 1; i <= n - 2; i++) printf()); printf(->0 ); }
D也是個構造,沒來及補