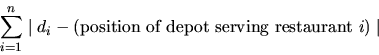程式師世界 >> 編程語言 >> C語言 >> C++ >> 關於C++ >> UVA 662 Fast Food(DP)

UVA 662 Fast Food(DP)

編輯：關於C++

The fastfood chain McBurger owns several restaurants along a highway. Recently, they have decided to build several depots along the highway, each one located at a restaurent and supplying several of the restaurants with the needed ingredients. Naturally, these depots should be placed so that the average distance between a restaurant and its assigned depot is minimized. You are to write a program that computes the optimal positions and assignments of the depots.

To make this more precise, the management of McBurger has issued the following specification: You will be given the positions of n restaurants along the highway as n integers 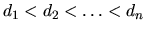$d_1 < d_2 < \dots < d_n$ (these are the distances measured from the company's headquarter, which happens to be at the same highway). Furthermore, a number 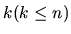$k (k \le? n)$ will be given, the number of depots to be built.

The k depots will be built at the locations of k different restaurants. Each restaurant will be assigned to the closest depot, from which it will then receive its supplies. To minimize shipping costs, the total distance sum, defined as

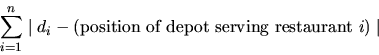
$\begin{displaymath}\sum_{i=1}^n \mid d_i - (\mbox{position of depot serving restaurant }i) \mid\end{displaymath}$

must be as small as possible.

Write a program that computes the positions of the k depots, such that the total distance sum is minimized.

Input

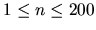
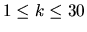
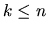
The input file contains several descriptions of fastfood chains. Each description starts with a line containing the two integers n and k. n and k will satisfy $1 \le? n\le? 200$ , $1 \le? k ?\le 30$ , $k \le n$ . Following this will n lines containing one integer each, giving the positions d_i of the restaurants, ordered increasingly.

The input file will end with a case starting with n = k = 0. This case should not be processed.

Output

For each chain, first output the number of the chain. Then output an optimal placement of the depots as follows: for each depot output a line containing its position and the range of restaurants it serves. If there is more than one optimal solution, output any of them. After the depot descriptions output a line containing the total distance sum, as defined in the problem text.

Output a blank line after each test case.

Sample Input

Sample Output

Chain 1
Depot 1 at restaurant 2 serves restaurants 1 to 3
Depot 2 at restaurant 4 serves restaurants 4 to 5
Depot 3 at restaurant 6 serves restaurant 6
Total distance sum = 8

考慮dp狀態為dp[i][j]:前i個酒店建k個倉庫的最小代價。 dp[i][j]=min(dp[k][j-1]+dis[k+1][i])(j-1<=k 關於路徑輸出設path[i][j]為達到dp[i][j]狀態的前一狀態的末倉庫。易知道path[i][1]=0; 其他的就是遞歸輸出了。

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
#define REPF( i , a , b ) for ( int i = a ; i <= b ; ++ i )
#define REP( i , n ) for ( int i = 0 ; i < n ; ++ i )
#define CLEAR( a , x ) memset ( a , x , sizeof a )
typedef long long LL;
typedef pairpil;
const int INF = 0x3f3f3f3f;
const int maxn=220;
int dis[maxn][maxn];
int dp[maxn][50];
int path[220][50];
int d[220];
int n,k,cnt;
int cal(int l,int r)
{
    int sum=0;
    int mid=(l+r)>>1;
    for(int i=l;i<=r;i++)
        sum+=abs(d[mid]-d[i]);
    return sum;
}
void print(int i,int x)
{
    if(x==0)
        return ;
    print(path[i][x],x-1);
    printf("Depot %d at restaurant %d serves restaurants %d to %d\n",x,(path[i][x]+1+i)/2,path[i][x]+1,i);
}
int main()
{
    int cas=1;
    while(~scanf("%d%d",&n,&k)&&(n+k))
    {
        CLEAR(dp,INF);
        CLEAR(path,0);cnt=1;
        REPF(i,1,n)  scanf("%d",&d[i]);
        for(int i=1;i<=n;i++)
            for(int j=1;j<=n;j++)
               dis[i][j]=cal(i,j);
        for(int i=1;i<=n;i++)
        {
            dp[i][1]=dis[1][i];
            path[i][1]=0;
        }
        for(int i=1;i<=n;i++)
        {
            for(int j=2;j<=k;j++)
            {
                for(int p=j-1;p