程式師世界 >> 編程語言 >> C語言 >> C++ >> 關於C++ >> BZOJ 1227 [SDOI2009] 虔誠的墓主人離線+樹狀數組+離散化

BZOJ 1227 [SDOI2009] 虔誠的墓主人離線+樹狀數組+離散化

編輯：關於C++

鳴謝：140142耐心講解縷清了我的思路

題意：由於調這道題調的頭昏腦漲，所以題意自己搜吧，懶得說。

方法：離線+樹狀數組+離散化

解析：首先深表本蒟蒻對出題人的敬(bi)意(shi)。這道題簡直喪心病狂，看完題後大腦一片空白，整個人都不好了，剛開始的思路是什麼呢？暴力思想枚舉每個墓碑，然後計算每個墓碑的虔誠度，然後再來統計。不過看看數據范圍呢？10^9*10^9的矩陣，最多才10^5個樹，光枚舉就已經超時了，所以肯定不行。(不過要是考試真沒思路我就那麼搞了- -！)

然後也想到來枚舉墓碑，不過還是些許猶豫，畢竟偏差較大，寫的話實現難。然後我就不知道怎麼搞了。

今天140142神犇耐心的給我講了大體的思路。

就是呢，把所有的點按x從大到小,x相同y從大到小排序，然後呢一個個來枚舉。

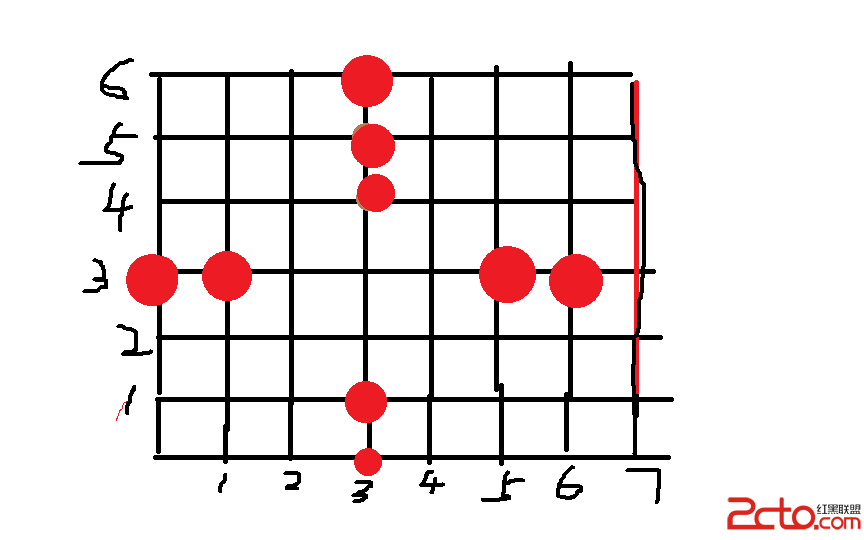
畫了個很sb的圖

用如上的圖來說。

先明確樹狀數組在本題是如何體現的。

首先這個樹狀數組存的值是什麼？

c[u[i]][K]?c[d[i]][K]其中，c是組合數，u[i]是對於i這個總坐標，當前的上面的樹的個數，d代表向下求。

現在這些點的順序應該已經排好了，那麼我來模擬一下正解的過程。

顯然第一個遍歷的點應該是[0，3]。

這時候我們能做什麼呢？統計他的左邊有多少點，右邊有多少點，當然，把他歸到左邊。為什麼？因為我們是從左到右處理，所以後面假設這一排還有點的話，[0,3]這個點當然在左邊。

統計完左右後，我們還能維護當前的上下，道理差不多吧。

經過很多的實驗，個人認為統計這些點上下左右最好用map來搞，非常實用。

以上就是第一個遍歷過程。

接下來，到[1,3]這個點，此時呢，這個點又到了新的一排，所以左右的話應該重新維護一下，而上下呢？顯然只是上–，下++。但是這時候就要注意了。在對上下進行操作之前，當前的樹狀數組顯然存的是[0,3]時候的值，所以我們要進行更新。而怎麼更新呢？

因為現在樹狀數組存的是c[u[3]][K]?c[d[3]][K]，

而我們要將之更新成c[u[3]?1][K]?c[d[3]+1][K]，也就是對應著上–，下++。為什麼要這麼做呢?

讓我們接著遍歷。

[3,0]這個點同樣換行了，所以維護左右，上下也填到樹狀數組。

[3,1]這個店沒有換行，所以左++，右–，上下填到樹狀數組。

關鍵就是到了[3,5]這個點。

我們可以看出，此時他與[3,1]之間是有3個點滿足題意的。那我們就要把這三個點的值加到答案上(其實[3,1]時也有這個過程，只不過它與上一個點緊挨著，所以不可能有解，被我跳過了)而這個加的值應該是什麼？

(∑i=24c[u[i]][K]?c[d[i]][K])?c[l[5?1]][K]?c[r[5?1]][K]

所以說，樹狀數組的作用就是維護這段區間的c[u[i]][k]?c[d[i]][k]的和的，只不過是多了動態更新，也就是每個點過後，都要重新更新樹狀數組的值。

樹狀數組的用法就說完了，如果沒懂，亦或是看看別人的題解，亦或是請教請教AC的人，亦或是理解理解上面這個求和公式。

接下來

圖中我特意留了幾個空行，我們發現，2,4,7這三列並沒有什麼卵用，完全可以刪除掉，不過這個刪除是必須的，因為10^9的邊長的矩形，咱們只算其中10^5個點，光是內存就開不下，所以離散化一下列，也就是縱坐標是必然的。

後記：我太弱

#include 
#include
#include 
#define N 100100
#define mod 2147483648ll
typedef long long ll ;
using namespace std ;
struct node
{
    int x ;
    int y ;
};
node a[N] ;
int n , m , K;
int w , tot;
map  M ;
map  line ;
map  line_x ;
ll c[N][11] ;
int yy[N] ;
int f[N] ;
int u[N] ;
ll sum[N] ;
int d[N] ;
int lowbit(int x)
{
    return x & (-x) ;
}
void update(int x , ll p)
{
    while(x <= tot)
    {
        sum[x] = (sum[x] + p)% mod ;
        x += lowbit(x) ;
    }
}
ll getsum(int x)
{
    ll ret = 0 ;
    while(x)
    {
        ret = (ret + sum[x])%mod ;
        x -= lowbit(x) ;
    }
    return ret ;
}
void init()
{
    c[0][0] = 1 ;
    for(int i = 1 ; i <= w ; i++)
    {
        c[i][0] = 1 ;
        int tmp = min(i , K) ;
        for(int j = 1 ; j <= tmp ; j++)
        {
            c[i][j] = (c[i-1][j] + c[i-1][j-1])%mod ;
        }
    }
}
bool cmp(node a , node b)
{
    if(a.x == b.x) return a.y < b.y ;
    return a.x < b.x ;
}
ll ans ;
int main()
{
    scanf("%d%d" , &n , &m) ;
    scanf("%d" , &w) ;
    for(int i = 1 ; i <= w ; i++)
    {
        scanf("%d%d" , &a[i].x , &a[i].y) ;
        yy[i] = a[i].y ;
        line[a[i].y] ++ ;
        line_x[a[i].x] ++ ;
    }
    scanf("%d" , &K) ;
    init() ;
    sort(a + 1 , a + w + 1 , cmp) ;
    sort(yy + 1 , yy + w + 1) ;
    yy[0] = -1 ;
    for(int i = 1 ; i <= w ; i++)
    {
        if(yy[i] != yy[i-1])
        {
            M[yy[i]] = ++tot ;
            f[tot] = yy[i] ;
        }
    }
    for(int i = 1 ; i <= tot ; i++)
    {
        u[i] = line[f[i]] ;
        d[i] = 0 ;
    }
    int tmp_line = -1 ;
    int l , r ;
    for(int i = 1 ; i <= w ; i++)
    {
        if(a[i].x != tmp_line)
        {
            tmp_line = a[i].x ;
            l = 1 , r = line_x[a[i].x] - 1 ;
            int ori = M[a[i].y] ;
            update(ori , (c[u[ori]-1][K]*c[d[ori]+1][K]%mod-c[u[ori]][K]*c[d[ori]][K]%mod)%mod) ;
            u[ori]-- ;
            d[ori]++ ;
        }else
        {
            ll S = getsum(M[a[i].y]-1) - getsum(M[a[i-1].y]) ;
            if(S < 0) S += mod ;
            ans = (ans + ((S*c[l][K])%mod * c[r][K])%mod)%mod ;
            l ++ , r-- ;
            int ori = M[a[i].y] ;
            update(ori , (c[u[ori]-1][K]*c[d[ori]+1][K]%mod-c[u[ori]][K]*c[d[ori]][K]%mod)%mod) ;
            u[ori] -- ;
            d[ori]++ ;
        }
    }
    printf("%lld\n" , ans) ;
}