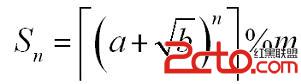程式師世界 >> 編程語言 >> C語言 >> C++ >> 關於C++ >> UVA 10655 Contemplation! Algebra（矩陣快速冪）

UVA 10655 Contemplation! Algebra（矩陣快速冪）

編輯：關於C++

Given the value of a+b and ab you will have to find the value of aⁿ+bⁿ

Input

The input file contains several lines of inputs. Each line except the last line contains 3 non-negative integers p, q and n. Here p denotes the value of a+b andq denotes the value of ab. Input is terminated by a line containing only two zeroes. This line should not be processed. Each number in the input file fits in a signed 32-bit integer. There will be no such input so that you have to find the value of 0⁰.

Output

For each line of input except the last one produce one line of output. This line contains the value of aⁿ+bⁿ. You can always assume that aⁿ+bⁿfits in a signed 64-bit integer.

Sample Input Output for Sample Input

10 16 2

7 12 3

0 0

Problem setter: Shahriar Manzoor, Member of Elite Problemsetters' Panel

Special Thanks: Mohammad Sajjad Hossain

題意很明顯就是求a^n+b^n；

我們發現f0=2,f1=a+b,f2=a^2+b^2=(a+b)*f1-a*b*f2....

依次遞推，令p=a+b,q=a*b;

所以fi=fi-1*p-fi-2*q;

構造出矩陣後就可以求解了。

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
#define REPF( i , a , b ) for ( int i = a ; i <= b ; ++ i )
#define REP( i , n ) for ( int i = 0 ; i < n ; ++ i )
#define CLEAR( a , x ) memset ( a , x , sizeof a )
typedef long long LL;
typedef pairpil;
const int INF = 0x3f3f3f3f;
struct Matrix{
    LL mat[2][2];
    void Clear()
    {
        CLEAR(mat,0);
    }
};
Matrix mult(Matrix m1,Matrix m2)
{
    Matrix ans;
    for(int i=0;i<2;i++)
        for(int j=0;j<2;j++)
        {
            ans.mat[i][j]=0;
            for(int k=0;k<2;k++)
                ans.mat[i][j]=ans.mat[i][j]+m1.mat[i][k]*m2.mat[k][j];
        }
    return ans;
}
Matrix Pow(Matrix m1,LL b)
{
    Matrix ans;ans.Clear();
    for(int i=0;i<2;i++)
        ans.mat[i][i]=1;
    while(b)
    {
        if(b&1)
           ans=mult(ans,m1);
        b>>=1;
        m1=mult(m1,m1);
    }
    return ans;
}
LL p,q,n;
int main()
{
    while(scanf("%lld%lld%lld",&p,&q,&n)==3)
    {
        Matrix A;
        if(n==0)
        {
            puts("2");
            continue;
        }
        if(n==1)
        {
            printf("%lld\n",p);
            continue;
        }
        A.mat[0][0]=p;A.mat[0][1]=-q;
        A.mat[1][0]=1;A.mat[1][1]=0;
        A=Pow(A,n-1);
        LL ans=A.mat[0][0]*p+A.mat[0][1]*2;
        printf("%lld\n",ans);
    }
    return 0;
}

HDU 4565

So Easy!

Problem Description 　　A sequence S_n is defined as:

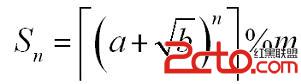
Where a, b, n, m are positive integers.┌x┐is the ceil of x. For example, ┌3.14┐=4. You are to calculate S_n.
　　You, a top coder, say: So easy!

Input 　　There are several test cases, each test case in one line contains four positive integers: a, b, n, m. Where 0< a, m < 2¹⁵, (a-1)²< b < a², 0 < b, n < 2³¹.The input will finish with the end of file.
Output 　　For each the case, output an integer S_n.
Sample Input

2 3 1 2013
2 3 2 2013
2 2 1 2013

Sample Output

4
14
4

題目要求這個式子答案，我們發現(a-1)^2<b<a^2這就意味著a-1<sqrt(b)<a; 所以又(a+sqrt(b))^n+(a-sqrt(b))^n為整數，所以式子答案即為(a+sqrt(b))^n+(a-sqrt(b))^n="" 簡化下，就是上面的a'="a+sqrt(b),b'=a-sqrt(b);所以p=2*a,q=a*a-b;" 問題轉化為上題做法。="" #include #include #include #include #include #include #include #include #include#include #include using namespace std; #define REPF( i , a , b ) for ( int i = a ; i <= b ; ++ i ) #define REP( i , n ) for ( int i = 0 ; i < n ; ++ i ) #define CLEAR( a , x ) memset ( a , x , sizeof a ) typedef long long LL; typedef pairpil; const int INF = 0x3f3f3f3f; struct Matrix{ LL mat[2][2]; void Clear() { CLEAR(mat,0); } }; LL a,b,n,m; Matrix mult(Matrix m1,Matrix m2) { Matrix ans; for(int i=0;i<2;i++) for(int j=0;j<2;j++) { ans.mat[i][j]=0; for(int k=0;k<2;k++) ans.mat[i][j]=(ans.mat[i][j]+m1.mat[i][k]*m2.mat[k][j])%m; } return ans; } Matrix Pow(Matrix m1,LL b) { Matrix ans;ans.Clear(); for(int i=0;i<2;i++) ans.mat[i][i]=1; while(b) { if(b&1) ans=mult(ans,m1); b>>=1; m1=mult(m1,m1); } return ans; } int main() { while(scanf("%I64d%I64d%I64d%I64d",&a,&b,&n,&m)!=EOF) { LL p=2*a,q=a*a-b;//x^n+y^n Matrix A; if(n==1) { printf("%I64d\n",p); continue; } A.mat[0][0]=p;A.mat[0][1]=-q; A.mat[1][0]=1;A.mat[1][1]=0; A=Pow(A,n-1); LL ans=A.mat[0][0]*p%m; ans=((ans+A.mat[0][1]*2)%m+m)%m; printf("%I64d\n",ans); } return 0; }