下面是差分約束系統的詳細介紹,以及解決方法~ 摘抄自 xuezhongfenfei(他好像也是轉的....)
差分約束系統
X1 - X2 <= 0
X1 - X5 <= -1
X2 - X5 <= 1
X3 - X1 <= 5
X4 - X1 <= 4
X4 - X3 <= -1
X5 - X3 <= -3
X5 - X4 <= -3
不等式組(1)
這個不等式組要麼無解,要麼就有無數組解。因為如果有一組解{X1, X2, ..., Xn}的話,那麼對於任何一個常數k,{X1 + k, X2 + k, ..., Xn + k}肯定也是一組解,因為任何兩個數同時加一個數之後,它們的差是不變的,那麼這個差分約束系統中的所有不等式都不會被破壞。
d(v) <= d(u) + w(u, v)
X1 - X0 <= 0
X2 - X0 <= 0
X3 - X0 <= 0
X4 - X0 <= 0
X5 - X0 <= 0
不等式組(2)
圖1 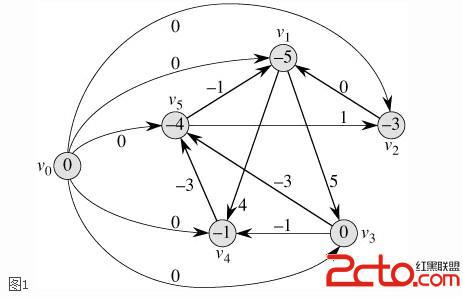
X0 = 0
d(v) >= d(u) + w(u, v)
也就是d(v) - d(u) >= w(u, v)
最近幾天系統得學習了一些差分約束系統的原理,特此記錄如下:
所謂差分約束系統,是指一組不定方程(A,x,T,b),其中A的每行有一個1,一個-1,其余為0,x為解向量,T為<=或>=組成的向量,b為約束矢量。具體來說,就是每行都具有 xi-xj >=|<= bi 的形式。約束的目標是使得目標函數xt-xs最大或最小。
這是典型的線性規劃的個案,但是也可以轉化為圖論來做,利用最短路(或最長路)方法可以實現高效的解決方案。
SPFA的介紹:
http://blog.csdn.net/u013382399/article/details/44227003
這樣最後再附上自己的代碼:
#include#include #include #include #include using namespace std; const int maxn = 110; const int INF = 0x3f3f3f3f; struct Edge{ int u,v,w,next; }edge[maxn*maxn]; int d[maxn],in[maxn],next[maxn]; bool vis[maxn]; int tot; int n,m; queue q; void addEdge(int u,int v,int w){ edge[tot].u = u; edge[tot].v = v; edge[tot].w = w; edge[tot].next = next[u]; next[u] = tot++; } bool spfa(int size){ int u,v; while(!q.empty()) q.pop(); memset(in,0,sizeof(in)); memset(vis,0,sizeof(vis)); fill(d,d+size,INF); d[n+1] = 0;vis[n+1] = true;in[n+1] = 1; q.push(n+1); while(!q.empty()){ u = q.front();vis[u] = false; q.pop(); for(int i = next[u]; i != -1; i = edge[i].next){ v = edge[i].v; if(d[u] + edge[i].w < d[v]){ d[v] = d[u] + edge[i].w; if(!vis[v]){ vis[v] = true; in[v] ++; if(in[v] > size) return false; q.push(v); } } } } return true; } int main(){ int si,ni,ki; char oi[5]; while(scanf(%d,&n)){ if(n == 0) break; scanf(%d,&m); memset(next,-1,sizeof(next)); tot = 0; ///自己創造一個超級原點,建立與其他點鏈接的邊(使其與其他點相連接) ///因為SPFA沒有辦法處理不連通的圖 for(int i = 0; i <= n; i++){ addEdge(n+1,i,0);///我讓點n+1作為一個超級源點,其余各節點的邊權是0 } for(int i = 1; i <= m; i++){ scanf(%d%d%s%d,&si,&ni,oi,&ki); if(oi[0] == 'g') addEdge(si+ni,si-1,-(ki+1)); if(oi[0] == 'l') addEdge(si-1,si+ni,ki-1); } if (spfa(n + 2)) printf(lamentable kingdom );///總共有n+2個點 else printf(successful conspiracy ); } return 0; }