Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.
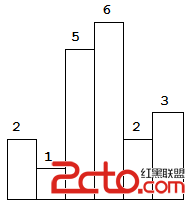
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].
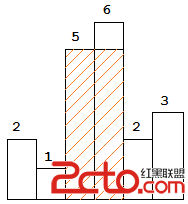
The largest rectangle is shown in the shaded area, which has area = 10 unit.
For example,
Given height = [2,1,5,6,2,3],
return 10.
Anwser 1: Brute Force
思路:窮舉法,對於直方圖的每一個bar, 我們窮舉所有的左邊界,將面積最大的那個記錄下來。時間復雜度為O(N^2).但是單純的窮舉法在leetcode會TLE. 所有我們需要一些剪枝的方法,比如找到合適的右邊界。我們發現當height[k] >= height[k-1]時,無論左邊界取什麼值,選擇height[k]作為右邊界總會比選擇height[k-1]所形成的面積大。因此,在選擇右邊界時,我們首先找到一個height[k] < height[k-1]的k, 然後取k-1作為右邊界,跳過中間的bar, 然後窮舉所有的左邊界,找到最大面積。
窮舉法還有一個思路,就是以當前bar為矩形高度,然後左右兩個指針分別向數組兩邊移動,直到高度低於當前bar高度截止,然後用當前bar的高度乘以兩邊走的寬度就是最大面積。因為我們對所有bar都計算了以自己為目標高度的最大矩陣,所以最好的結果一定會取到。但是同樣,未經剪枝的還是超時。
Attention:
1. 窮舉時,我們需要維護一個從當前k 向前的最小高度。
int lowest = height[i];
for(int j = i; j >= 0; j--)
{
lowest = min(height[j], lowest);
2. 注意剪枝的方法
for(int k = i + 1; k < height.size(); k++)
{
if(height[k] < height[k-1])
{
i = k - 1;
break;
}
else
{
i = k;
}
}
AC Code:
class Solution {
public:
int largestRectangleArea(vector &height) {
int maxarea = 0;
for(int i = 0; i < height.size(); i++)
{
for(int k = i + 1; k < height.size(); k++)
{
if(height[k] < height[k-1])
{
i = k - 1;
break;
}
else
{
i = k;
}
}
int lowest = height[i];
for(int j = i; j >= 0; j--)
{
lowest = min(height[j], lowest);
int curarea = lowest * (i - j + 1);
maxarea = max(maxarea, curarea);
}
}
return maxarea;
}
};
思路:我們維護一個棧,這個棧從低向上的高度依次是遞增的,如果遇到當前bar的高度比棧頂元素低,那麼就出棧直到滿足條件,這個過程中,我們不斷把出棧的棧頂元素當做最低高度計算最大面積。關鍵問題在於出棧時,如何確定出棧元素所對應的高度的最大范圍是多少。如果棧為空,那麼說明到目前為止的所有元素(當前下標元素除外)都比出棧元素高度要大(否則棧內還會有元素),那麼矩陣面積就是棧頂元素高度h[t] * 當前下標i . 如果棧不為空,那麼就是從當前棧頂元素的下一個到當前下標元素之前都比出棧元素高度要大,因為當前棧頂元素是第一個比出棧元素小的。具體可以看下這幅圖:
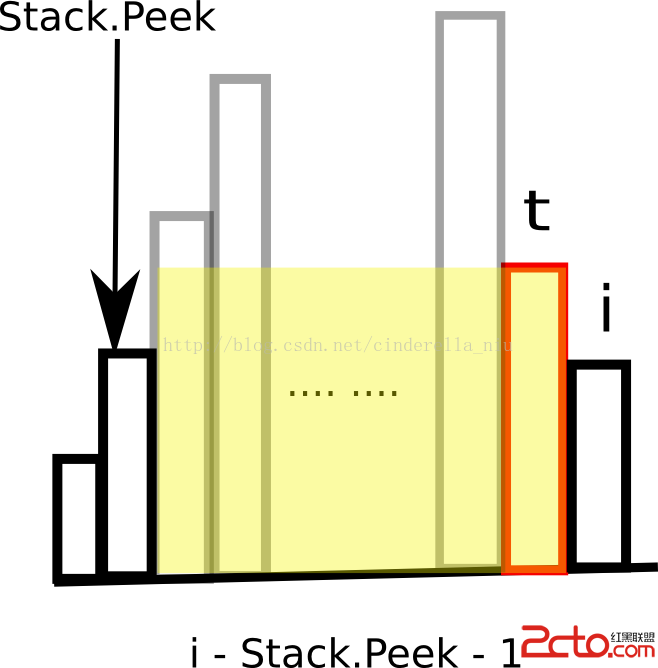
另外一個細節需要注意的是,彈棧過程中面積的計算。
h[t] * (stack.isEmpty() ? i : i - stack.peek() - 1)
h[t]是剛剛彈出的棧頂端元素。此時的面積計算是h[t]和前面的“上流社會”能圍成的最大面積。這時候要注意哦,棧內索引指向的元素都是比h[t]小的,如果h[t]是目前最小的,那麼棧內就是空哦。而在目前棧頂元素和h[t]之間(不包括h[t]和棧頂元素),都是大於他們兩者的。
我們需要注意的是,最後要對剩下的棧做清空並判斷,因為算法每次是對於前面的元素面積進行判斷,如果循環結束後如果棧內仍然有元素,還是要繼續維護面積直到棧為空。AC Code:
class Solution {
public:
int largestRectangleArea(vector &height) {
stack stk;
int maxarea = 0;
int tp; //棧頂元素
int area_with_tp; //存儲以棧頂元素作為最短板的面積
int i = 0;
while(i < height.size())
{
if(stk.empty() || height[i] >= height[stk.top()])
stk.push(i++);
else
{
tp = stk.top();
stk.pop();
area_with_tp = height[tp] * (stk.empty() ? i : i - stk.top() - 1);
maxarea = max(maxarea, area_with_tp);
}
}
//如果棧仍然非空 繼續處理
while(!stk.empty())
{
tp = stk.top();
stk.pop();
area_with_tp = height[tp] * (stk.empty() ? i : i - stk.top() - 1);
maxarea = max(maxarea, area_with_tp);
}
return maxarea;
}
};
這道題還有個擴展題目 Maximal Rectangle, 利用這道題作為子程序,是一道比較復雜的題目。