程式師世界 >> 編程語言 >> C語言 >> C++ >> 關於C++ >> UVA10214 Trees in a Wood. 歐拉phi函數

UVA10214 Trees in a Wood. 歐拉phi函數

編輯：關於C++

只看某一個象限能看到的數 == 一個象限*4+4

能看到的樹既距離原點的距離 gcd(x,y)==1

a 和 b 一大一小預處理2000以內的phi函數,枚舉小的一條邊

從1...a 與 a gcd 為 1 的數的個數就是 phi(a)

從 1+a ... 2*a 與 a gcd 為 1 的數的個數因為 GCD(i,a) = GCD(i+a,a) 所以還是 phi(a)

....

Trees in a Wood. Time Limit: 3000MS Memory Limit: Unknown 64bit IO Format: %lld & %llu

Submit Status

Description

Problem H
Trees in a Wood.
Input: Standard Input
Output: Standard Output
Time Limit: 10 seconds

Background

The saying ``You can't see the wood for the trees'' is not only a cliche, but is also incorrect. The real problem is that you can't see the trees for the wood. If you stand in the middle of a wood, the trees tend to obscure each other and the number of distinct trees you can actually see is quite small. This is especially true if the trees are planted in rows and columns, because they tend to line up. The purpose of this problem is to find how many distinct trees one can see if one were standing on the position of a tree in the middle of the wood.

The Problem

For a mathematically more precise description we assume that you are situated at the origin of a coordinate system in the plane.

Trees are planted at all positions , with "x|<=a and |y|<=b .

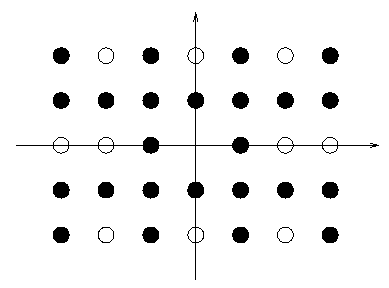
A tree at pZ喎?/kf/ware/vc/" target="_blank" class="keylink">vc2l0aW9uICh4LHkpIGNhbiBiZSBzZWVuIGZyb20gdGhlIG9yaWdpbiBpZiB0aGVyZSBhcmUgbm8gb3RoZXIgdHJlZXMgb24gdGhlIHN0cmFpZ2h0IGxpbmUgZnJvbSAoMCwwKSB0byAoeCx5KSAuIEZpbmQgdGhlIG51bWJlciBLIG9mIGFsbCB0aGUgdHJlZXMgaW4gdGhlIHdvb2QgdGhhdCBjYW4gYmUgc2VlbiBmcm9tIHRoZSBvcmlnaW4gYW5kIHRoZSBudW1iZXIgTiBvZiBhbGwgdGhlIHRyZWVzIHRvCiBjb21wdXRlIHRoZSBmcmFjdGlvbiA8aW1nIHNyYz0="https://www.aspphp.online/bianchen/UploadFiles_4619/201701/2017010315323995.gif" width="19" height="29" id="_x0000_i1027" align="top" border="0" alt="\">.

Hint: The Euler phi function is defined to be the number of integers m in the range 1≤m≤n relatively prime to n :

Instead of counting (an adequate method for small n !) you could as well use the following identity:

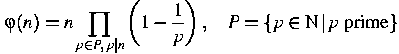
Hint: Remember that gcd (m,n)= gcd (m+n,n)= gcd (m+2n,n)= gcd (m+in,i)

You might be surprised that the fraction converges to 0.607927 for an infinitely large wood.

The Input

Each scenario consists of a line with the two numbers a and b (separated by a white space), with 1 <= a <= 2000 and 1 <= b <= 2000000 Input is terminated by a line with two zeros.

The Output

For each scenario print a line containing the fraction with a precision of 7 digits after the decimal point. Error less than 2e-7 or 2*10^(-7) will be tolerated.

Sample Input

3 2
0 0

Sample Output

0.7058824

Collected from TUD Programming Contest

Source

Root :: AOAPC II: Beginning Algorithm Contests (Second Edition) (Rujia Liu) :: Chapter 10. Maths :: Examples

Submit Status

/* ***********************************************
Author        :CKboss
Created Time  :2015年02月03日 星期二 22時13分33秒
File Name     :UVA10214.cpp
************************************************ */

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;

int gcd(int a,int b)
{
	return (b==0)?a:gcd(b,a%b);
}

int phi[2200];
int GCD[2020][2020];

void phi_table(int n)
{
	phi[1]=1;
	for(int i=2;i<=n;i++)
	{
		if(!phi[i])
		{
			for(int j=i;j<=n;j+=i)
			{
				if(!phi[j]) phi[j]=j;
				phi[j]=phi[j]*(i-1)/i;
			}
		}
	}
}

void init()
{
	phi_table(2010);
	for(int i=1;i<=2000;i++)
		for(int j=1;j<=2000;j++)
			if(GCD[i][j]==0)
				GCD[i][j]=GCD[j][i]=gcd(i,j);
}

int a,b;

int main()
{
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);

	init();
	while(scanf("%d%d",&a,&b)!=EOF)
	{
		if(a==0&&b==0) break;
		if(a>b) swap(a,b);
		double ret=0;
		for(int i=1;i<=a;i++)
		{
			int duan = b/i;
			int yu = b%i;
			ret += duan * phi[i];
			for(int j=1;j<=yu;j++)
			{
				if(GCD[j][i]==1)
					ret+=1;
			}
		}
		ret = ret*4 + 4;
		double all = (2.*a+1)*(2.*b+1)-1.;
		double ans = ret/all;
		printf("%.7lf\n",ans);
	}
    
    return 0;
}