A簽到題排序之後貪心一下就可以了。
const int maxn = 10010;
using namespace std;
struct node
{
int pos;
int num;
}f[maxn];
bool cmp(node a, node b)
{
return a.num < b.num;
}
int p[maxn];
int main()
{
int n, k;
while(cin >>n>>k)
{
for(int i = 0; i < n; i++)
{
cin >>f[i].num;
f[i].pos = i+1;
}
sort(f, f+n, cmp);
int ans = 0;
for(int i = 0; i < n; i++)
{
if(k < f[i].num) break;
p[ans++] = f[i].pos;
k -= f[i].num;
}
cout<
B主要是策略每次沿著兩個圓心的連線轉就可以了,所以次數就是距離dis/2*r,注意處理精度,最後一組的好多人掛在精度上了。
const int maxn = 10010;
using namespace std;
int main()
{
double r, x1, y1, x2, y2;
while(cin >>r>>x1>>y1>>x2>>y2)
{
double dis = sqrt((x1-x2)*(x1-x2)*1.0 + 1.0*(y1-y2)*(y1-y2));
LL xp = dis/(2.0*r);
///cout<<"st == "<
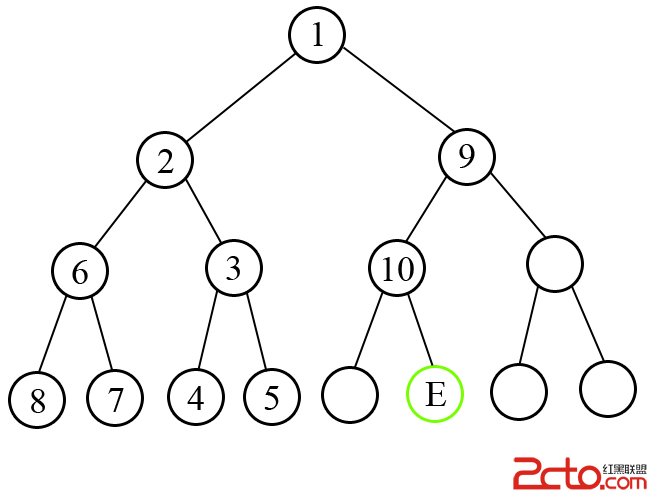
C樣例的圖解釋的很清楚了,按層枚舉之後你會發現規律,先判斷葉子的位置是在這一層的根節點的哪一邊,如果第k層的根節點x是奇數左子樹是的根節點是x+1,否則是x+2^(h-k+1),如果x是偶數那就反過來。
由於我的根節點是從一開始的,不要忘記了判斷最後一層就可以了啊。
C. Guess Your Way Out!
time limit per test
1 second
memory limit per test
256 megabytes
input
standard input
output
standard output
Amr bought a new video game "Guess Your Way Out!". The goal of the game is to find an exit from the maze that looks like a perfect binary tree of height h.
The player is initially standing at the root of the tree and the exit from the tree is located at some leaf node.
Let's index all the leaf nodes from the left to the right from 1 to 2h.
The exit is located at some node n where 1?≤?n?≤?2h,
the player doesn't know where the exit is so he has to guess his way out!
Amr follows simple algorithm to choose the path. Let's consider infinite command string "LRLRLRLRL..." (consisting of alternating characters 'L'
and 'R'). Amr sequentially executes the characters of the string using following rules:
-
Character 'L' means "go to the left child of the current node";
-
Character 'R' means "go to the right child of the current node";
-
If the destination node is already visited, Amr skips current command, otherwise he moves to the destination node;
-
If Amr skipped two consecutive commands, he goes back to the parent of the current node before executing next command;
-
If he reached a leaf node that is not the exit, he returns to the parent of the current node;
-
If he reaches an exit, the game is finished.
Now Amr wonders, if he follows this algorithm, how many nodes he is going to visit before reaching the exit?
Input
Input consists of two integers h,?n (1?≤?h?≤?50, 1?≤?n?≤?2h).
Output
Output a single integer representing the number of nodes (excluding the exit node) Amr is going to visit before reaching the exit by following this algorithm.
Sample test(s)
input
1 2
output
2
input
2 3
output
5
input
3 6
output
10
input
10 1024
output
2046
Note
A perfect binary tree of height h is a binary tree consisting of h?+?1 levels.
Level 0 consists of a single node called root, level h consists
of2h nodes called leaves.
Each node that is not a leaf has exactly two children, left and right one.
Following picture illustrates the sample test number 3. Nodes are labeled according to the order of visit.
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
output
4
input
2 2 1000
output
45
input
5 3 1103
output
590
Note
A suffix of a string S is a non-empty string that can be obtained by removing some number (possibly, zero) of first characters from S.
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
