[算法設計與分析]最小生成樹，貪心算法實現

/**
* 書本:《算法分析與設計》
* 功能:實現用Prim算法實現尋找最小生成樹
* 文件:PrimMixTree.cpp
* 時間:2015年1月4日19:42:57
* 作者:cutter_point
*/

#include 
#include 		//文件輸入輸出流

using namespace std;

const int N = 6;		//這個圖是一個6*6的矩陣
const int inf = 9999;

ifstream fin("prim.txt");		//輸入文件源

//核心算法
template
void Prim(int n, T c[][N+1])		//輸入節點個數和圖的矩陣
{
	T lowcost[N + 1];	//記錄S到V-S(N+1)的最短距離，記錄c[j][closest]的最小權值，就是已經選中為最短路徑的部分到沒選中額部分的最短距離
	int closest[N + 1];		//V-S中點j在S中的最近鄰接頂點 ，這個是節點，上面那個是權值距離
	bool s[N + 1];

	s[1] = true;

	//S就是最小生成樹的組成
	for (int i = 2; i <= n; ++i)		//初始化所有的數組
	{
		lowcost[i] = c[1][i];	//就是1到其他節點的距離就是當前的最短距離，應為首先我們，默認從1開始
		closest[i] = 1;		//連接的是S中的1號節點，因為開始的時候S中只有1
		s[i] = false;		//首先從2開始都不是S中的元素
	}

	//開始尋找最小生成樹
	for (int i = 1; i < n; ++i)	//一共還有5個節點
	{
		T min = inf;		//初始是沒有連接，所以是9999，假設是無窮
		int j = 1;	//標記這個是要新加入的節點

		for (int k = 2; k <= n; ++k)		//遍歷所有的節點
		if ((lowcost[k] < min) && (!s[k]))		//找到還沒有被選中的節點中，S到他們的距離是找到最小的一條lowcost[k]就是S中到k節點的最小值
		{
			min = lowcost[k];		//找到最小的一條路
			j = k;		//得到這個節點
		}
		//輸入找到的路徑
		cout << "把" << j << "連接上" << closest[j] << endl;
		s[j] = true;		//把j節點加入到最小生成樹中

		//重新更新lowcost和closest
		for (int k = 2; k <= n; ++k)
		{
			//S到k的距離和當前要連接的節點j到k相比那個小，把小的作為新的各個節點V-S到S的最小路徑
			if ((c[j][k] < lowcost[k]) && (!s[k]))		//必須是外面沒加入到最小生成樹的節點
			{
				lowcost[k] = c[j][k];		//刷新S到V-S（k)的最短路徑
				closest[k] = j;		//S和V-S連接最近節點的改變
			}
		}
	}

}

int main()
{
	int c[N + 1][N + 1];			//+1是為了後面輸入的時候從1開始到6，而不是從0到5

	cout << "圖的矩陣是：" << endl;
	for (int i = 1; i <= N; ++i)
	{
		for (int j = 1; j <= N; ++j)
		{
			fin >> c[i][j];		//把文件中的數據輸入到數組中
			cout << c[i][j] << "\t";		//輸出看看
		}
		cout << endl;
	}

	cout << "生成最小生成樹尋找次序：" << endl;
	Prim(N, c);


	return 0;
}

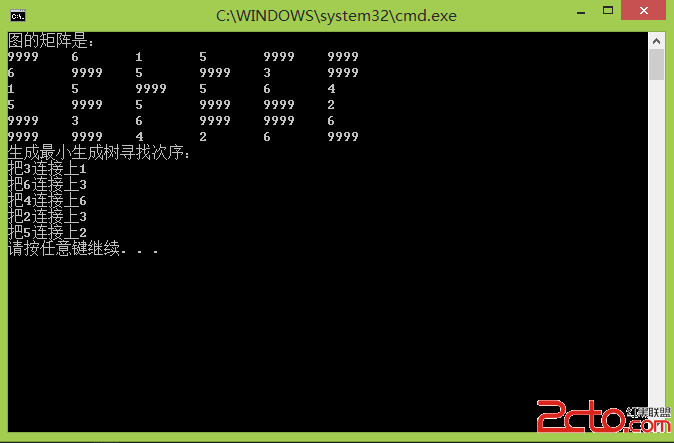
效果截圖：