上一篇博客寫到了如何給一個非終結符的文法規則構造出一個壓縮過的下推狀態機,那麼今天說的就是如何把所有的文法都連接起來。其實主要的idea在(三)和他的勘誤(三點五)裡面已經說得差不多了。但是今天我們要處理的是帶信息的transition,所以還有一些地方要注意。
所以在這裡我們先把幾條文法的最後的狀態機都列出來(大圖):
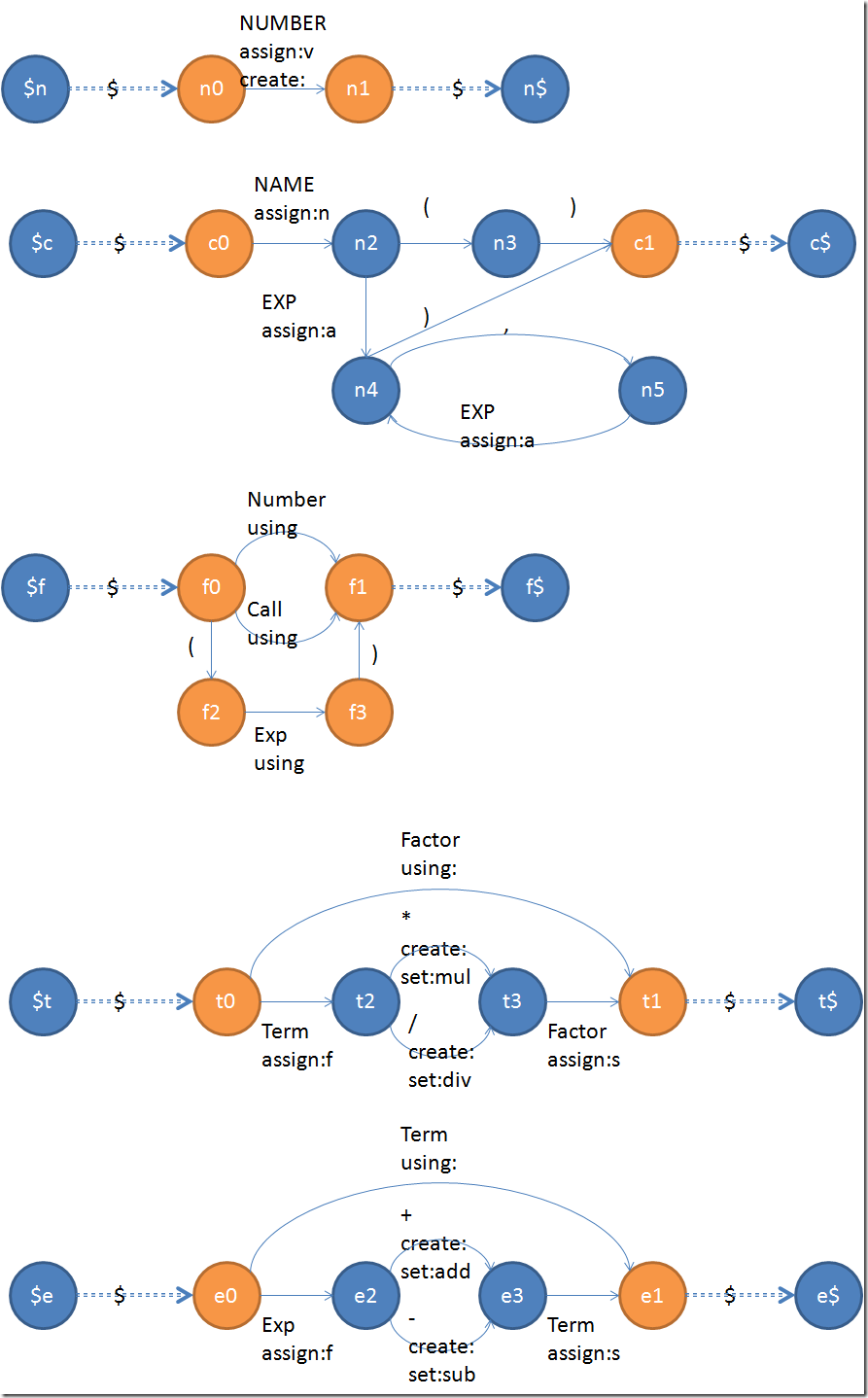
本欄目
接下來的這一步,就是要對所有靠非終結符(Exp啊Term這些)進行跳轉的transition都執行上一篇文章所說的傳說中的交叉鏈接。在產生鏈接的時候,我們給shift和reduce的邊分別加上shift和reduce。而shift和reduce是有參數的——就是被shift走的狀態的id。這樣可以在parse的時候匹配和處理狀態堆棧。在這裡我門對e3->e1這一步做一下操作做為例子。紅色的邊是被刪掉的,而粗壯的綠色邊是被新加進去的:
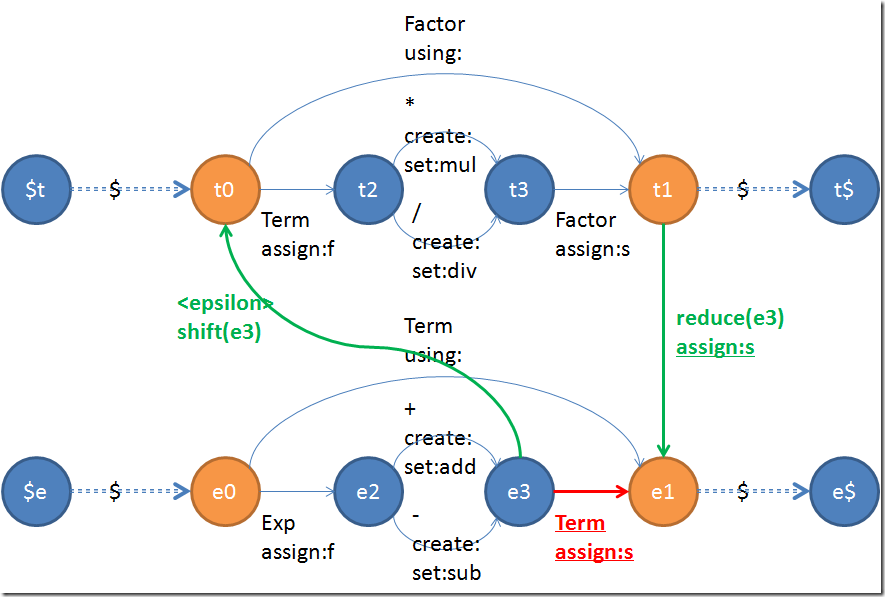
紅色的邊變成了兩條綠色的邊,紅色的邊附帶的信息則被復制到了綠色的reduce邊上。當我們使用這個狀態機的時候,shift(s3)就表示往堆棧裡面壓入s3,reduce(s3)就表示從堆棧裡面彈出(s3)。當然彈出不一定會成功,所以如果不成功的話,這條邊就不能在當時使用。因此這也就是為什麼在e3跳轉到t0之後,t1知道往回跳的是e1而不是別的什麼地方——就如同為什麼C++的函數執行完之後總是知道如何跳轉回調用它的地方一樣——因為把信息推入了堆棧。
本欄目
在添加shift和reduce邊之前,每一條邊都是有輸入token的。但是我們剛剛添加上去的shift和reduce邊卻是不輸入token的,所以他們是epsilon邊,下一步就是要消除他們。上面這個圖消除了epsilon邊之後,會變成一個狀態很少,但是每一條邊附帶的信息都會非常多,而且像n1這種經常到達的狀態(因為四則運算裡面有很多數字)將恢復射出無數條邊。到了這裡這個狀態機已經再也畫不出來了。所以我下面就只拿兩個例子來畫。下面要展示的是用Exp來parse單獨的一個數字會走的邊,當然就是Exp –> Term –> Factor –> Number了:
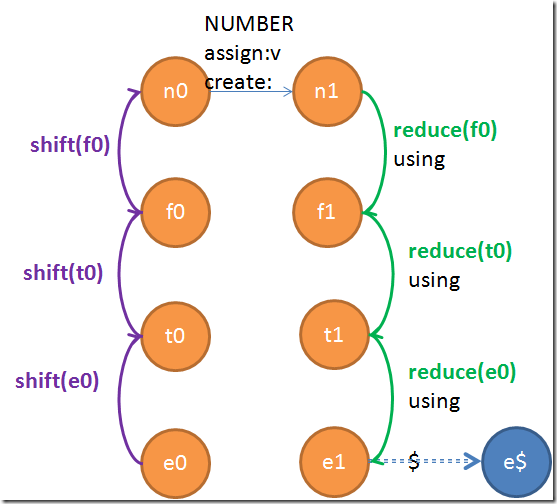
就會被處理成:
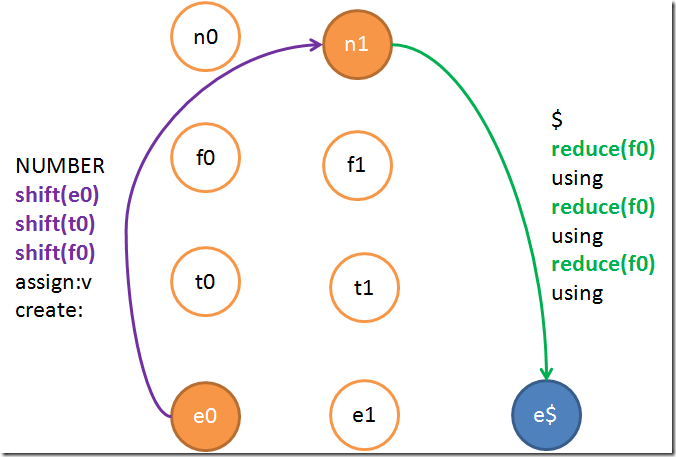
注意邊上面的信息是要按順序重新疊加在一起的。當所有的epsilon邊都去掉了之後,我們就得到了最終的一個狀態機。最重要的一件事情出現了。我們知道,發明LR和LALR這種東西就基本上是為了處理左遞歸的,所以這種圖就可以在去除epsilon邊的過程中自動發現左遞歸。這是怎麼做到的呢?只要在去除epsilon邊的時候,發現了一條完全由shift這種epsilon邊組成的環,那麼左遞歸就發現了。為了方便,我們可以只處理直接左遞歸——就是這種環的長度是1的。不包含間接左遞歸的問法是很容易寫出來的。當然這種環並不一定是首尾相接的,譬如說我們在處理e0的時候就會發現e0->t0->t0這種環(當然嚴格來說環只有最後一截的這個部分)。我們的程序要很好地應對這種情況。因為我們只接受直接左遞歸,所以類似這種結構的epsilon路徑可以直接的拋棄他,因為t0->t0會被t0狀態單獨處理掉。因此這樣做並不會漏掉什麼。
細心的朋友可能會發現,這個結構的圖是不能直接處理右遞歸的(總之左遞歸和右遞歸總要有一個會讓你的狀態機傻逼就是了!)。關於如何處理有遞歸(其實內容也不復雜)地方法會在“下篇”描述出來。那處理左遞歸有什麼用呢?舉個例子,我們的e0->e2就是一個左遞歸,而他會在之前的步驟被處理成shift(e0->e0)和reduce(e1->e2)。我們要記下shift和reduce的對應關系,那麼當我們找到一個左遞歸的shift之後,我們就可以把對應的reduce給標記成“left-recursive-reduce”。這是一個在構造語法樹的時候,非常關鍵的一種構造指令。
處理完這些之後,我們可以把左遞歸的shift邊全部刪掉,最後把token和state都統統處理成連續的數字,做成一張[state, token] –> [transitions]的二維表,每一個表的元素是transition的列表。為什麼是這樣呢?因為我們對一個state輸入一個token之後,由於保存著state的堆棧(你還記得嗎?shift==push,reduce==pop)的棧頂若干個元素的不同,可能會走不通的路線。於是最後我們就得到了這麼一張圖。
下面這張圖可以通過運行gac.codeplex.com上面的Common\UnitTest\UnitTest.sln(VS2012限定)之後,在Common\UnitTest\TestFiles\Parsing.Calculator.Table.txt裡面找到。這一組文件都是我在測試狀態機的時候log下來的。
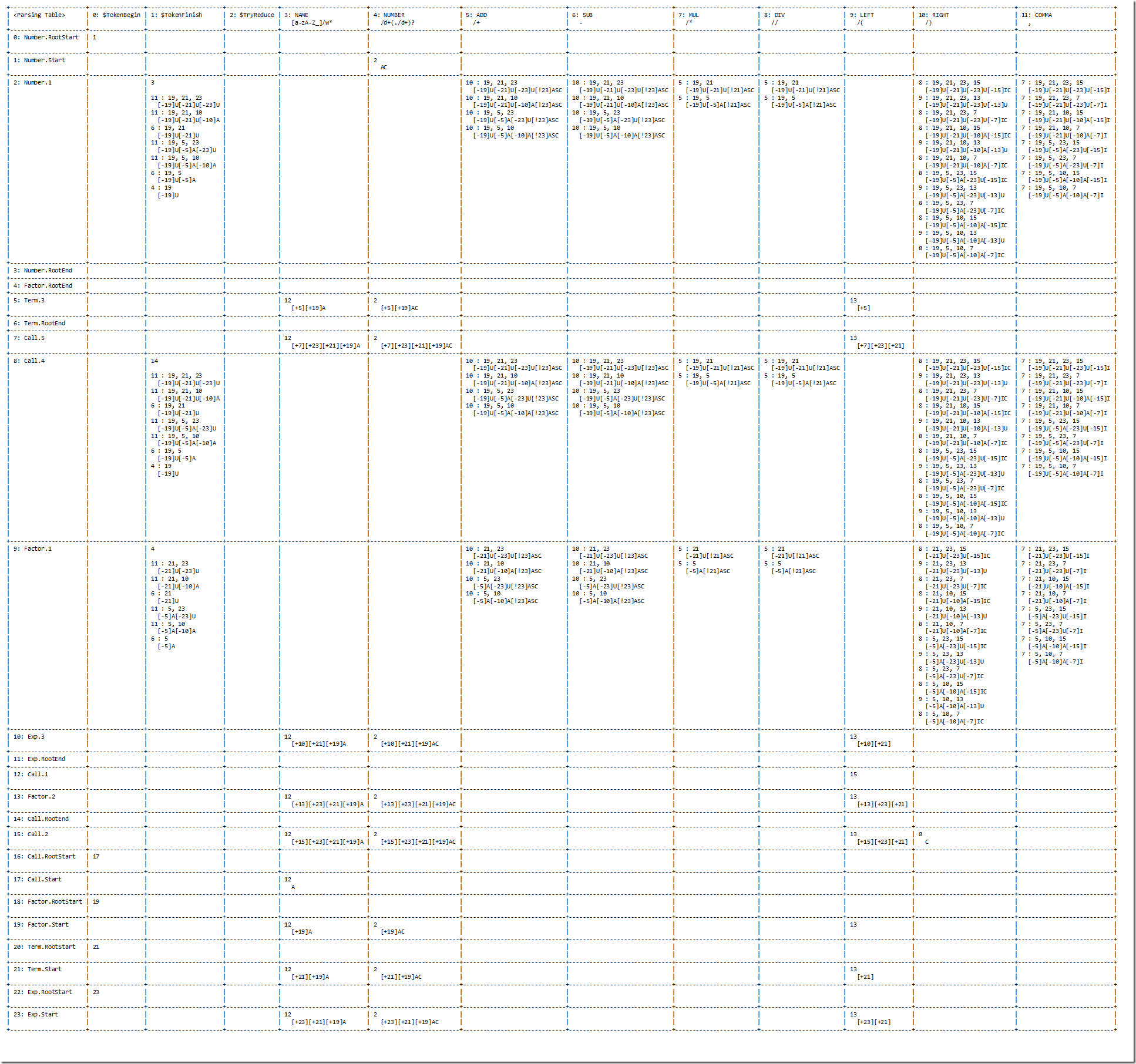
如果大家有VS2012的話,通過運行我准備的幾個輸入,譬如說“1*2+3*4”,就可以在Parsing.Calculator.[2].txt裡面找到所有狀態跳轉的軌跡。因為我們總是需要parse一個Exp,所以我們從22: Exp.RootStart開始。我們假設token stream的第一個和最後一個分別是$TokenBegin和$TokenFinish。上圖的$TryReduce是為了應對右遞歸而設計出來的一種特殊輸入。由於四則運算裡面並沒有右遞歸,所以這一列就是空的:
StartState: 22[Exp.RootStart]
$TokenBegin => 23[Exp.Start]
State Stack:
NUMBER[1] => 2[Number.1]
State Stack: 23[Exp.Start], 21[Term.Start], 19[Factor.Start]
Shift 23[Exp]
Shift 21[Term]
Shift 19[Factor]
Assign value
Create NumberExpression
MUL[*] => 5[Term.3]
State Stack: 23[Exp.Start]
Reduce 19[Factor]
Using
Reduce 21[Term]
Using
LR-Reduce 21[Term]
Assign firstOperand
Setter binaryOperator = Mul
Create BinaryExpression
NUMBER[2] => 2[Number.1]
State Stack: 23[Exp.Start], 5[Term.3], 19[Factor.Start]
Shift 5[Term]
Shift 19[Factor]
Assign value
Create NumberExpression
ADD[+] => 10[Exp.3]
State Stack:
Reduce 19[Factor]
Using
Reduce 5[Term]
Assign secondOperand
Reduce 23[Exp]
Using
LR-Reduce 23[Exp]
Assign firstOperand
Setter binaryOperator = Add
Create BinaryExpression
NUMBER[3] => 2[Number.1]
State Stack: 10[Exp.3], 21[Term.Start], 19[Factor.Start]
Shift 10[Exp]
Shift 21[Term]
Shift 19[Factor]
Assign value
Create NumberExpression
MUL[*] => 5[Term.3]
State Stack: 10[Exp.3]
Reduce 19[Factor]
Using
Reduce 21[Term]
Using
LR-Reduce 21[Term]
Assign firstOperand
Setter binaryOperator = Mul
Create BinaryExpression
NUMBER[4] => 2[Number.1]
State Stack: 10[Exp.3], 5[Term.3], 19[Factor.Start]
Shift 5[Term]
Shift 19[Factor]
Assign value
Create NumberExpression
$TokenFinish => 11[Exp.RootEnd]
State Stack:
Reduce 19[Factor]
Using
Reduce 5[Term]
Assign secondOperand
Reduce 10[Exp]
Assign secondOperand
本欄目