GradientFill函數可以對特定的矩形區域或者三角形區域進行漸變顏色的填充。我們先來看看GradientFill函數到底長得什麼樣子,帥不帥。
BOOL GradientFill( _In_ HDC hdc, _In_ PTRIVERTEX pVertex, _In_ ULONG nVertex, _In_ PVOID pMesh, _In_ ULONG nMesh, _In_ ULONG ulMode );
參數涉及結構體,於是有些人就開始感到痛苦了,調用函數一遇到結構體就會痛苦,而這個函數更痛苦,還要結構體的數組。
人家達摩祖師說了,痛苦是你的事,和API無關,它又不會因為你痛苦就變得簡單易用,該簡單的就簡單,該復雜的還是那麼復雜。我們來分析一個吧。首先第一個hdc就不用我說了,就是某個上下文,這個上下文你就理解為和誰有關,就是誰的句柄,句柄是一種資源標識,以前說過了,就好比身份證號碼可以唯一標識你的身份一般(假身份證除外)。所以,這個hdc就是決定你要把漸變顏色畫到哪裡,畫到窗口上就是窗口的HDC,畫到桌面上就是桌面的HDC。
第二個參數,注意,是TRIVERTEX結構體的數組,數組中每一個TRIVERTEX結構體的變量指定一個漸變點的坐標和顏色,顏色是ARGB四通道的,也就是說你可以玩透明效果,A,R,G,B每個值的范圍,MSDN上有說明是The color information of each channel is specified as a value from 0x0000 to 0xff00,這個范圍用十進制表示到底是多少,自己打開“計算器”算一下就知道了,Win7以後的計算器程序嚴重強大,用來算命都可以,更別說進制換算了。
如果你寫C++程序多了,你就會猜到第三個參數是什麼了,凡是涉及到傳數組作為參數的,後面肯定要帶一個參數指明數組中有多少個元素。因為C語言的數組與托管語言不同,其實它是善變的,你定義了int a[3] ....,然後你賦值的時候,賦到a[5]都可以,雖然會報錯,但是你不妨試試,即使報錯,但是仍然可以取到值,因為內存分布是連續的。
不用說,nVertex 就是指明前面pVertex的個數;後面一個pMesh又是一個結構體的數組,但它是“雄雌同體”的,可以是GRADIENT_TRIANGLE結構體的數組,也可以是GRADIENT_RECT結構體的數組,具體得看你想怎麼填充,從名字就知道,GRADIENT_TRIANGLE是三角形填充,就是填充出來的區域是三角形的,這個應該好理解,就是你的內褲的形狀;而GRADIENT_RECT更好理解了,矩形,就是小學老師教你的長方形,正方形。
接著這個nMesh 參數你肯定知道了,不解釋了,你懂的。
最後一個參數就是指定怎麼填充,無非就是水平填過去,還是垂直填下來之類的。
那麼,TRIVERTEX數組與GRADIENT_RECT或GRADIENT_TRIANGLE數組是如何對應的呢?
GRADIENT_TRIANGLE是定義三角形的,要確定一個三角形就得要三個點,所以這些點就從TRIVERTEX數組來,每個TRIVERTEX變量定義一個點。
比如,TRIVERTEX數組有六個元素,就有六個點,剛好可以定義兩個三角形,GRADIENT_TRIANGLE中的三個成員就是三角形三個點的索引,這些索引就是TRIVERTEX數組中的元素的索引,六個點,索引是0,1,2,3,4,5,接著,如果第一個GRADIENT_TRIANGLE中的三個成員分別設為0,1,2,則六個點中前三個點就定義了第一個三角形,如果第二個GRADIENT_TRIANGLE的三個成員設置為3,4,5,那麼,六個點中的後三個點組成一個三角形。如果是1,4,5,就說明六個點中的第二個,第五個和第六個點將組成一個三角形。
GRADIENT_RECT就更好理解了,兩個點就可以確定一個矩形,即左上角的點,右下角的點,如果漸變點有四個,正好可以組成兩個矩形。0和1,2和3.
下面的代碼將畫出兩個矩形的填充區域。
case WM_PAINT:
hdc = BeginPaint(hWnd, &ps);
// TODO: 在此添加任意繪圖代碼...
TRIVERTEX trives[4];
trives[0].x=10;
trives[0].y=12;
trives[0].Alpha=0xff00;
trives[0].Red=0xe100;
trives[0].Green=0x00cc;
trives[0].Blue=0xa3c3;
trives[1].x=188;
trives[1].y=80;
trives[1].Alpha=0xff00;
trives[1].Red=0x00fa;
trives[1].Green=0x0068;
trives[1].Blue=46;
trives[2].x=280;
trives[2].y=190;
trives[2].Alpha=0xff00;
trives[2].Red=0x0004;
trives[2].Green=0x0017;
trives[2].Blue=0xff00;
trives[3].x=500;
trives[3].y=320;
trives[3].Alpha=0xff00;
trives[3].Red=0xfac0;
trives[3].Green=0xcccc;
trives[3].Blue=0xcef0;
// 定義漸變區為矩形,並確定其點
GRADIENT_RECT rects[2];
rects[0].UpperLeft=0;
rects[0].LowerRight=1;
rects[1].UpperLeft =2;
rects[1].LowerRight=3;
GradientFill(hdc,trives,4,rects,2,GRADIENT_FILL_RECT_H);
EndPaint(hWnd, &ps);
break;
最後就得到如下圖所示的效果。
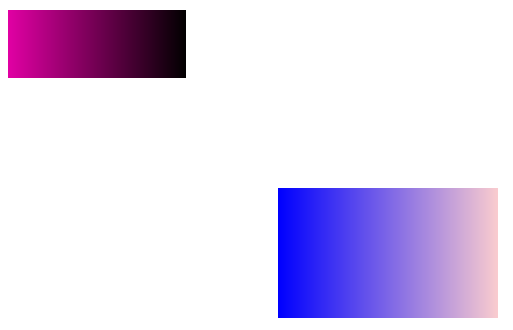
好,下面我們看看三角形的。
// 三角形
GRADIENT_TRIANGLE triangles[2];
triangles[0].Vertex1=2;
triangles[0].Vertex2=0;
triangles[0].Vertex3=3;
triangles[1].Vertex1=3;
triangles[1].Vertex2=1;
triangles[1].Vertex3=0;
// 矩形填充
GradientFill(hdc,trives,4,rects,2,GRADIENT_FILL_RECT_V);
// 三角形填充
GradientFill(hdc,trives,4,triangles,2,GRADIENT_FILL_TRIANGLE);
我們用的還是前面填充矩形的四個點,那有人會問了,不對啊,四個怎麼能弄出兩個三角形呢,不是應該要六個點嗎?是啊,是六個點,但是這個四個點是可以重復利用,現在都說要環保,所以循環利用,2-0-3組成一個三角形,3-1-0又組成一個三角形。反正就是一個排列組合,你只要每個三角形弄足三個點就行了。前面的矩形同樣道理,你只要每個矩形弄夠兩個點就行了。這就很像WPF中使用的三角形建模的三維圖形同理,點的集合我就定義這麼多個,但是我在其中任取三個就可以組成一個“模型單元”。
與前面的代碼合並執行,最後得到這種效果。
