矩陣:
矩陣是數值程序設計中經常用到的數學模型,它是由 m 行和 n 列的數值構成(m=n 時稱為方陣)。在用高級語言編制的程序中,通常用二維 數組表示矩陣,它使矩陣中的每個元素都可在二維數組中找到相對應的存儲位置 。然而在數值分析的計算中經常出現一些有下列特性的高階矩陣,即矩陣中有很 多值相同的元或零值元,為了節省存儲空間,需要對它們進行"壓縮存儲 ",即不存或少存這些值相同的元或零值元。
操作:可以對矩陣作 加、減、乘等運算。
存儲壓縮目標:
節約存儲空間
壓縮 的方法:
零元不存儲
多個值相同的只存一個
壓縮存儲的 對象:
稀疏矩陣
特殊矩陣
特殊矩陣:
值相同元素 或者零元素分布有一定規律的矩陣稱為特殊矩陣 例:對稱矩陣、 上(下)三角 矩陣都是特殊矩陣
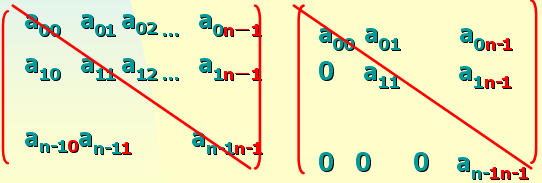
特殊矩陣壓縮存儲(以對稱矩陣為例)
對稱矩陣是滿足下面條 件的n 階矩陣: aij= aji 1<= i,j<= n
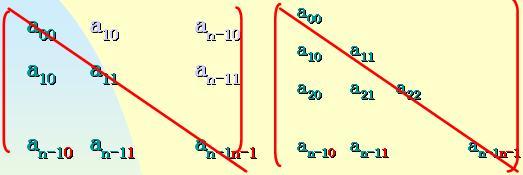
![]()
k= 0 1 2 3 4 5 6 n(n+1)/2-1
對稱矩陣元素可以只存儲 下三角部分,共需 n(n+1)/2 個單元的空間( 三角矩陣的存儲方式類似)
以一維數組sa[0……n(n+1)/2-1]作為n 階對稱矩陣A的 存儲結構A中任意一元素 aij與它的存儲位置 sa[k] 之間關系:
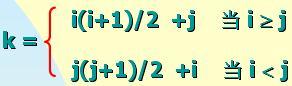
![]()
k= 0 1 2 3 4 5 6 n(n+1)/2-1
例如:a42 在 sa[ ]中的 存儲位置是:
k=4*(4+1)/2+2=12
sa[12]= a42
帶狀矩陣 所有非0元素都集中在以主對角線為中心的帶狀區域,半帶寬為d時, 非0元素有 (2d+1)*n-(1+d)*d個(左上角與右下角補上0後,最後必須減掉),如下圖 怕示:

為計算方便,認為每一行都有2d+1個非0元素,若少則0補足存放矩陣 的數組sa[ ]有:n(2d+1)個元素數組,元素sa[k]與矩陣元素aij 之間有關系 :
k=i*(2d+1)+d+(j-i)(第一項i*(2d+1)表示前i行一共有幾個元 素,d+(j-i)這一項是用來確定第i行中,第j列前有幾個元素,以i=j時,這時 j-i=0,這個作為“分水嶺”,左右兩邊的元素分別加上偏移量d.)

本例:d=1
K= 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
![]()
(a0前以及a14處放一個0是用來表示在矩陣的左上角及右下角補上的0 )
稀疏矩陣:

行數m = 6, 列數n = 7, 非零元素個數t = 6稀疏矩陣 (SparseMatrix)的抽象數據類型
template <class Type>
class SparseMatrix ...{
int Rows, Cols, Terms; //行/列/非零元素數
Trituple<Type> smArray[MaxTerms];
public: //三元組表
SparseMatrix ( int MaxRow, int Maxcol );
SparseMatrix<Type> Transpose ( ); //轉置
SparseMatrix<Type> //相加
Add ( SparseMatrix<Type> b );
SparseMatrix<Type> //相乘
Multiply ( SparseMatrix<Type> b );
}
A的三元組順序表圖示

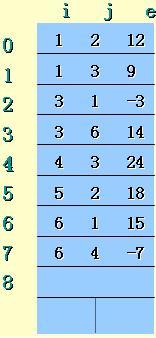
三元組 (Trituple) 類的定義
template<class Type> class SparseMatrix<Type>;
template<class Type>
class Trituple ...{
friend class SparseMatrix <Type>
private:
int row, col; //非零元素所在行號/列號
Type value; //非零元素的值
}
稀疏矩陣

轉置矩陣
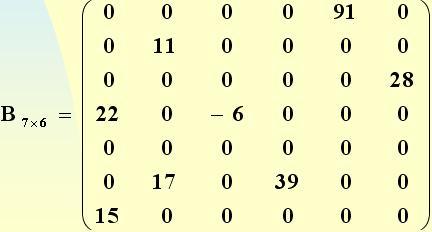
用三元組表表示的稀疏矩陣及其轉置:
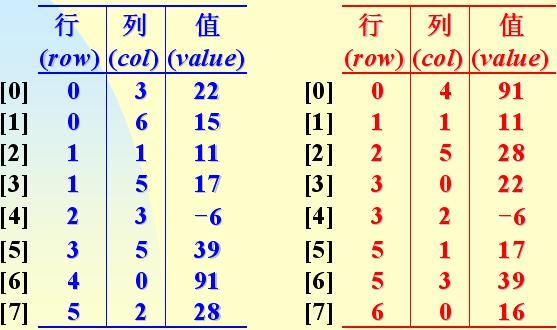
a.smArray b.smArray
(a.Rows=6,a.Cols=7,a.Terms=8 ) (b.Rows=7,b.Cols=6,b.Terms=8)
稀疏矩 陣轉置算法思想
對應上圖的一個最簡單的方法是把三元組表中的row與 col的內容互換,然後再按照新的row中的行號對各三元組從小到大重新排序,最 後得到上圖右半部分的三元組表,但是用這樣的方法其時間復雜度為平方級的, 下面再用一種方法來處理:假設稀疏矩陣A有n列,相應地,需要針對它的三元組 表中的col列進行n次掃描,第k次掃描是在數組的col列中查找列號為k的三元組 ,若找到,則意味著這個三元組所表示的矩陣元素在稀疏矩陣的第k列,需要把 它存放到轉置矩陣的第k行。具體辦法是:取出這個三元組,並交換其row(行號 )與col(列號)的內容,連同value中存儲的值,作為新三元組存放到矩陣的三 元組表中。當n次掃描完成時,算法結束。程序清單如下:
稀疏矩陣的轉 置
template <class Type> SparseMatrix <Type> SparseMatrix <Type>:: Transpose ( ) ...{
//將稀疏矩陣a(*this指示)轉置,結果在稀疏矩陣b中。
SparseMatrix<Type> b ( Cols, Rows ); //創建一 個稀疏矩陣類的對象b
b.Rows = Cols; b.Cols = Rows; //交換其row(行號 )與col(列號)的內容,連同value
b.Terms = Terms; //中存儲的值作為新三元組放到矩陣的三元組 表中。
if ( Terms > 0 ) ...{ //非零元個數不為零
int CurrentB = 0; //轉置三元組表存放指針
for ( int k = 0; k < Cols; k++ ) //按列號做掃描,做 cols次
for ( int i = 0; i < Terms; i++ ) // 在數組中找列號為k的三元組
if ( smArray[i].col == k) ...{ //第i個三元組中元素的列號為k
b.smArray[CurrentB].row = k; //新三元組的行號
b.smArray [CurrentB].col=smArray[i].row; //新三元組的列號
b.smArray [CurrentB].value=smArray[i].value; //新三元組的值
CurrentB++; //存放指針加 1
}
}
return 0;
}
若設稀疏矩陣的行數為Rows,列數為Cols,非 零元素個數為Terms,則最壞情況下的時間復雜度主要取決於二重潛套for循環內 的if語句,if語句在二重循環的作用下總的執行次數為O(Cols*Terms)。而在 if控制內的賦值語句則執行了Terms次,它取決於三元組表本身的長度。若非零 元素個數Terms與矩陣行,列數的乘積Rows*Cols等數量級,則上述程序清單的時 間復雜度為O(Cols*Terms)=O(Rows*Cols*Cols)。設Rows=500,Cols=100, Terms=10000,則O(500*100*100)=O(5000 000),處理效率極低。
為 了提高轉置效率,采用一種快速轉置的方法。在此方法中,引入兩個輔助數組:
1. rowSize[].用它存放事先統計出來的稀疏矩陣各列的非零元素個數, 轉置以後是轉置矩陣各行的非零元素個數。具體做法是:先把這個數組清零,然 後掃描矩陣A的三元組表,逐個取出三元組的列號col,把以此列號為下標的輔助 數組元素的值累加1.
for(int i=0;i<Cols;i++) rowSize[i]=0; //清零
for(j=0;j<Terms;j++) rowSize[smArray[j].col]++;// 統計,注意這裡用到的簡潔的算法
2. rowstart[].用它存放事先計算出 來的稀疏矩陣各行非零元素在轉置矩陣的三元組表中應存放的位置。
rowSize[0]=0;//計算矩陣b第i行非零元素的開始存放位置
for (i=1;i<Cols;i++)rowStart[i]=rowStart[i-1]+rowSize[i-1]
快 速轉置算法的思想
·建立輔助數組 rowSize 和 rowStart,記錄 矩陣轉置後各行非零元素個數和各行元素在轉置三元組表中開始存放位置。
·掃描矩陣三元組表,根據某項的列號,確定它轉置後的行號, 查 rowStart 表,按查到的位置直接將該項存入轉置三元組表中。
·轉置時間代價為O(max(Terms, Cols))。若矩陣有200 列 ,10000個非零元素,總共需要10000次處理。
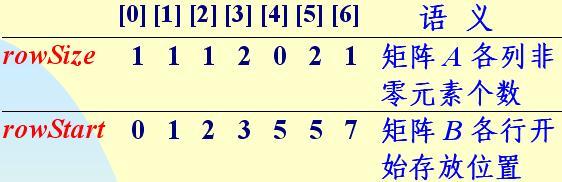
對應上圖的代碼在就像前面所列的:
for ( int i = 0 ; i < Cols; i++ ) rowSize[i] = 0;
for ( i = 0; i < Terms; i++ )
rowSize[smArray[i].col]++;
rowStart[0] = 0 ;
for ( i = 1; i < Cols; i++ )
rowStart[i] = rowStart[i-1]+rowSize[i-1];
稀疏矩陣的快速轉置
template <class Type> SparseMatrix<Type>
SparseMatrix<Type>::FastTranspos ( ) ...{
//對稀疏矩陣a(*this指示)做快速轉置,結果放在b中,時間代價 為O(Terms+Columns)。
int *rowSize = new int[Cols]; //輔助數組,統計各列 非零元素個數
int *rowStart = new int[Cols]; //輔助數組,預計轉 置後各行存放位置
SparseMatrix<Type> b ( Cols, Rows ); //存放 轉置結果
b.Rows = Cols; b.Cols = Rows;
b.Terms = Terms;
if ( Terms > 0 ) ...{
for (int i = 0; i < Cols; i++) rowSize [i] = 0; //統計矩陣b中第i行非零元素個數
for ( i = 0; i < Terms; i++ )
//根據矩陣a中第i個非零元素的列號,將rowSize相當該列的計數 加1
rowSize[smArray[i].col]++;
rowStart[0] = 0; //計算矩陣b第i行非零元素的開始存放位置
for ( i = 1; i < Cols; i++ ) //rowStart[i]=矩陣b的第i行的開始存放位置
rowStart[i] = rowStart[i-1]+rowSize [i-1];
for ( i = 0; i < Terms; i++ ) ...{ //從a向b傳送
int j = rowStart[smArray[i].col]; //j為第i個非零元素在b中應存放的位置
b.smArray[j].row = smArray[i].col;
b.smArray[j].col = smArray[i].row;
b.smArray[j].value = smArray [i].value;
rowStart[smArray[i].col]++;
}
}
delete[ ] rowSize; delete [ ] rowStart;
return b;
}
在此程序中有4個並列循環,其時間復雜度分別為 O(Cols),O(Terms),O(Cols),和O(Terms),則程序總的時間復雜度為 O(Cols+Terms)。當Terms與Rows*Cols等數量級時,程序的時間復雜度為O (Cols+Terms)=O(Rows*Cols)。設Rows=500,Cols=100,Terms=10000, 則O(500*100)=O(50000)。當Terms遠遠小於Rows*Cols時,此程序會更省時 間,但程序中需要增加兩個體積為Cols的輔助數組。一般Terms總是大於Cols的 ,如果能夠大幅度提高速度,這點空間存儲上的開銷是值得的。