1 引言
排序是計算機數據處理及其它許多軟件系統中常用的一種操作。排序的目的通常是為了便於查找或為了適應某些查找算法的需要。例如,在統計高考成績的系統中,要產生幾個表。第一個表按考生的考號從小到大的順序,列出所有考生的成績;第二個表按考生的考試成績從高到低的順序,列出所有考生的成績等等。在這樣的系統中就要多次進行排序操作。
排序(Sorting)是把一個無序的數據元素序列按某個關鍵字進行有序(遞增或遞減)排列的過程。通常,待排序的操作對象稱為數據表,它是數據元素(即記錄)的有限集合。在每一個數據元素中有多個屬性。當某個屬性用來區分對象作為排序的依據時,該屬性就稱為排序關鍵字(Key)。如上例中的考號、考試成績等都是排序關鍵字。在實際應用中,每個數據表用哪個屬性作為排序關鍵字要視具體的應用需要而定。
排序的方法很多,就其全面的性能而言,很難提出一種被認為是最好的方法,每種方法都各有優缺點,適合在不同的環境下使用。就其時間的性能而言,插入排序、冒泡排序、選擇排序性能比較接近,而快速排序、堆排序、歸並排序則是性能比較接近的另一類。
2 堆排序的原理與技術
堆排序是改進的算法,比較復雜。記錄數越多越適合,效率可以明顯提高。堆排序是借助於一種稱為堆的完全二叉樹結構進行排序的,排序過程中,將向量中存儲的數據看成是一棵完全二叉樹的順序存儲結構,利用完全二叉樹中的父結點和子結點之間的內在關系來選擇關鍵字最小或最大的記錄。
具體做法是:把待排序的記錄存放在數組r[1‥n]中,將r看作一棵二叉樹,每個結點表示一個記錄,第一個記錄r[1]作為二叉樹的根,以後各記錄r[2],…,r[n]依次逐層從左到右順序排列,構成一棵完全二叉樹,任意結點r[i]的左孩子是r[2i],右孩子是r[2i+1],雙親是r[i/2]。對這棵完全二叉樹的結點進行調整,使各結點的關鍵字滿足條件,r[i]≤r[2i]且r[i]≤r[2i+1],即每個結點的值均小於或等於它的兩個子結點的值,顯然在這個堆樹中根結點的關鍵字最小,這種堆被稱為“小根堆”。若各結點的值滿足r[i]≥r[2i]並且r[i]≥r[2i+1]的堆,稱為“大根堆”,大根堆中根結點的關鍵字值最大。
在堆中,根結點又被稱為堆頂元素,當把二叉樹轉換成大根堆後,堆頂元素最大,把堆頂元素輸出,重新調整二叉樹的剩余結點,使其成為一個新堆,再輸出堆頂元素,便可求得次最大值,如此反復進行,就可得到一個有序序列,這就是利用大根堆排序的基本方法。小堆根的排序方法類似。
堆排序的關鍵是構造堆,即調整元素間的關系使之形成堆。由二叉樹的性質得知,二叉樹中序號最大的一個非終點是[n/2],序號最小的列終結點是序號為1的結點,對這些結點需一一進行調整,使其滿足堆的條件。調整過程為:首先把[n/2]號結點元素與其兩個孩子中值大者進行比較並交換後,形成以[n/2]為根的子樹即為堆,接著用相同的步驟對第[n/2-1]結點進行調整,直至第1個結點。如果在中間調整過程中,由於交換破壞了以其孩子為根的堆,則要對破壞了的堆進行調整,依次類推,直到父結點大於等於左、右孩子的元素結點或者孩子結點為空的元素結點。當這一系列調整過程完成時,即成為一個堆樹,這個調整過程也叫做“篩選”。
3 堆排序的實現3.1 堆排序在成績管理中的實現
下面給出學生的考試成績表,如圖1所示。每條信息由考號與分數組成。以按分數高低次序來排出每個學生在考試中獲得的名次,分數相同的為同一名次為例,說明堆排序的算法。
這裡,二叉樹中序號最大的一個非終點是[n/2],即圖中的4號結點268.5,序號最小的列終結點是序號為1的結點,即根結點270.0。調整過程為:首先把4號結點元素268.5與其兩個孩子中值大者進行比較,由於左孩子272.5>268.5故將它們交換,則以272.5為根的子樹即為堆。接著用相同的步驟對第3個結點進行調整,因其滿足條件,則不必交換。直至第1個結點270.0,最終形成初始堆,如圖3。
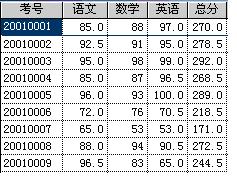
圖1 學生考試成績表
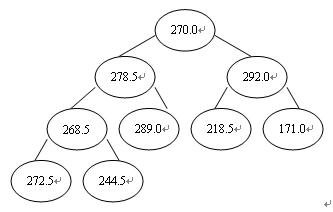
圖2 原始數據的二叉樹順序存儲形
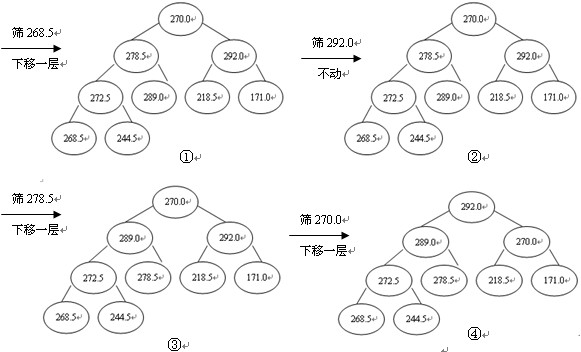
圖3 建立初始堆
排序過程為:先輸出堆頂元素292.0,把它放到原數組的最後位置,而原數組最後一個單元存放的是244.5,為了不破壞數據,則把292.0與244.5交換,即r[1]與r[n](n為9)交換,這時r[n]為最大,接著對r[1]與r[n-1]進行篩選又得到新堆,此時新堆的r[1]為當前最大的元素,再把r[1]與r[n-1]對調,使r[n-1]為次最大,這樣,經過n-1次對調、篩選,數組r中的所有元素均按升序排列,堆排序全部完成,如圖4所示。
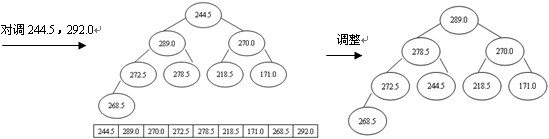
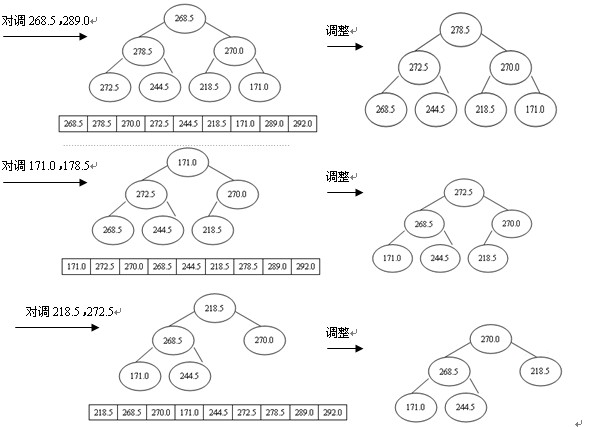
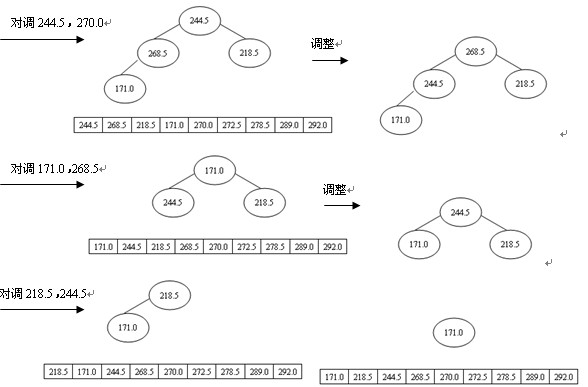
圖4 堆排序的過程
3.2 堆排序的算法描述
下面給出整個排序過程及算法描述。(說明:已經有序的子樹部分省去。)
heapsort (Recordnode r[ ],int n)
{int i,k;
Struct Recordnode x;
For(i=n/2;i>0;i--) /*建立初始堆*/
Sift(r,i,n);
For(i=n;i>1;i--) /*進行n-1次循環,完成堆排序*/
{ x=r[1]; /*將第一個元素與當前區間的最後一個元素對調*/
r[1]=r[i];
r[i]=x;
sift(r,1,i-1); /*調用篩選子函數*/
}
}
4 結束語
從堆排序的算法知道,堆排序所需的比較次數是建立初始堆與重新建堆所需的比較次數之和,其平均時間復雜度和最壞的時間復雜度均為O(n lbn)。它是一種不穩定的排序方法。
但對應於大量記錄,堆排序的效率卻是非常高的。
參考文獻
[1](美)Sartaj Sahni ,汪詩林,孫曉東等譯.數據結構、算法與應用——C++語言描述.機械工業出版社,2001
[2] 高一凡.《數據結構》算法實現及解析.西安電子科技大學出版社,2004
收稿日期:7月11日 修改日期:8月27日
作者簡介:尹聰春(1975-),女,東北財經大學職業技術學院計算機教研室,講師,研究方向:計算機網絡技術、嵌入式開發技術。