我們在學習有限元課程時做的另一個作業，用 C/C++ 編程求解了一個簡單的有限元問題，可以作為有限元學習的編程實例，以更好地理解有限元理論，並為進一步使用大型有限元軟件打下基礎。本文所涉及的有限元基本理論請參考章本照先生編著的《流體力學中的有限元方法》PP.156-165。
一、二維傳熱問題
如圖一所示：
圖一 二維傳熱問題
二、解題過程
1、對結構進行離散化，將待分析的結構物從幾何上用線或面劃分為有限個單元，按結構物的不同和分析要求，選取不同形式的單元，在單元的邊界上設置節點，並書寫編號。計算節點坐標
2、單元分析：設法導出單元的結點位移和結點力之間的關系，建立單元剛度矩陣。
單元剛度矩陣的計算：
對於方程
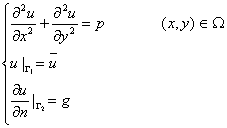
采用 Galerkin弱解表達式
（*）
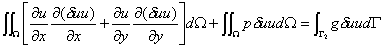這裡采用三節點的三角形單元，單元的基函數共有三個，選用插值多項式
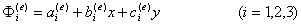
分別代入單元三個節點的坐標可解得
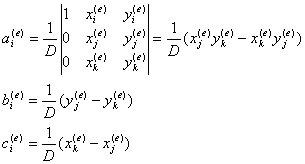
其中
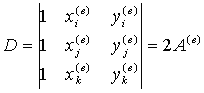
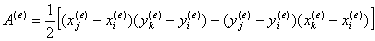
e單元中的近似函數為
（**）
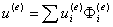將式（*）中的積分區域取為e單元的區域 ，並將單元中的近似函數表達式（**）代入，並注意到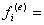
的任意性，可得
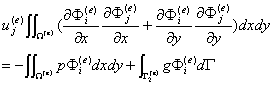
記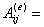 
（***）
（****）
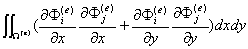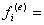
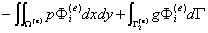將單元基函數的具體表達式（*）代入（***）式中，可得
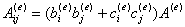
通過等參變換（具體見文獻1第201頁），可得
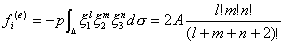
這裡指p為常數的情況，A為三角形單元的面積。
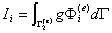
這裡g 均為0，所以此項不用計算。
3、整體分析（以求結點力為例）整體分析就是將各個單元組成結構整體進行分析。整體分析的目的在於導出整個結構結點位移與結點力之間的關系，建立整個結構的剛度方程。分析步驟：首先按著一定的集成規則，將各單元剛度矩陣集合成結構整體剛度矩陣，並將單元等效結點荷載集合成整體等效結點荷載列陣；然後引入結構的位移邊界條件，求解整體平衡方程組，得出基本未知量――結點位移列陣。
4、用選定的算法語言編寫出程序（C/C++），調試程序調用高斯消元法解方程的出結果。
附件程序Fem1.cpp計算了積分值，Fem2.cpp則采用了面積坐標下的插值函數，積分值取為三角形面積的三分之一。兩者結果相同，但是後者更為通用，可以把程序用於其他形狀的二維區域的有限元計算，Fem3.cpp計算了題2。
三．單元網格劃分
四邊形單元網格劃分單元網格劃分示意如圖一：
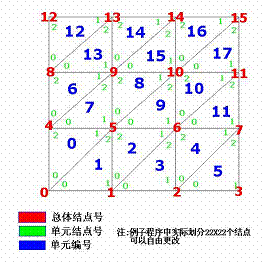
圖一
計算結果結果數據可視化如圖二、圖三。它們是題1分別用Fem1.cpp程序和Fem2.cpp程序計算結果的Matlab數據可視化圖，它們表現的數據基本一致，觀察視點不同。圖4是題2的解。
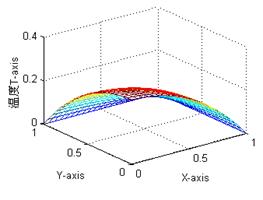
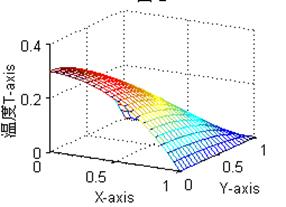
圖二 圖三
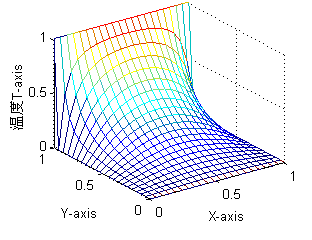
圖四
利用此程序的基本框架，我們還成功地解算了三角形、橢圓形區域的有限元問題。
最後感謝我們的老師----在數學和計算上具有深厚功力的王旭教授，感謝他對我們的悉心指導和熱情鼓勵！
本文配套源碼
