看過這樣一道題,問,“程序結構化設計的三種基礎結構,順序、選擇、循環是不是必須的?”當然,你知道這樣一個論斷,只要有這三種就足夠了;但是能不能更少呢?答案是“可以”,原因就是遞歸能取代循環的作用,例如下面的對一個數組裡面元素求和的函數:
float rsum (float a[], const int n)
{
if (n <= 0) return 0;
else return rsum(a, n – 1) + a[n – 1];
}
實際上就是:
sum = 0;
for (int i = 0; i < n; i++) sum += a[i];
但實際的情況是,任何的一種語言裡面都有循環結構,但不是任何的語言都支持遞歸;套用一句話,遞歸是萬能的,但沒有遞歸不是萬萬不能的。然而,我看到現在的某些人,不管什麼問題都要遞歸,明明循環是第一個想到的方法,偏偏費盡腦筋去尋找遞歸算法。對此,我真的不知道該說什麼。
遞歸是算法嗎
經常的看到“遞歸算法”、“非遞歸算法”,這種提法沒有語義上的問題,並且我自己也這樣用——遞歸的算法。但這也正說明了,遞歸不是算法,他是一種思想,正是因為某個算法的指導思想是遞歸的,所以才被稱為遞歸算法;而一個有遞歸算法的問題,當你不使用遞歸作為指導思想,這樣得到的算法就是非遞歸算法。——而對於循環能處理的問題,都有遞歸解法,在這個意義上說,循環算法都可以稱為非遞歸算法。
我在這咬文嚼字沒什麼別的意思,只是想讓大家知道,能寫出什麼樣的算法,關鍵是看你編寫算法時的指導思想。如果一開始就想到了循環、迭代的方法,你再費心耗神去找什麼遞歸算法——即使找到了一種看似“簡潔”的算法,由於他的低效實際上還是廢物——你還在做這種無用功干什麼?典型的學究陋習。如果你僅僅想到了遞歸的方法,現在你想用棧來消解掉遞歸,你做的工作僅僅是把系統做的事自己做了,你又能把效率提高多少?盲目的迷信消解遞歸就一定能提高效率是無根據的——你做的工作的方法如果不得當的話,甚至還不如系統原來的做法。
從學排列組合那天開始,我所知道的階乘就是這個樣子n! = 1×2×……n。如果讓我來寫階乘的算法,我也只會想到從1乘到n。再如,斐波那契數列,如果有人用自然語言描述的話,一定是這樣的,開始兩項是0、1,以後的每項都是前面兩項的和。所以讓我寫也只會得到“保存前兩項,然後相加得到結果”的迭代解法。——現在只要是講到遞歸幾乎就有他們的登場,美其名曰:“定義是遞歸的,所以我們寫遞歸算法”。我想問的是,定義的遞歸抽象是從哪裡來的?顯然階乘的定義是從一個循環過程抽象來的,斐波那契數列的定義是個迭代的抽象。於是,我們先從一個本不是遞歸的事實抽象出一個遞歸的定義,然後我們說,“因為問題的定義是遞歸的,因此我們很容易寫出遞歸算法”,接著說,“我們也能將這個遞歸算法轉化為循環、迭代算法”,給人的感覺就像是1÷3=0.33……,0.33……×3=0.99……,然後我們花了好大的心智才明白1=0.99……。
還是有那麼些人樂此不疲,是凡講到遞歸就要提到這兩個,結果,沒有一個學生看到階乘那樣定義沒有疑問的,沒有一個對於那個遞歸的階乘函數抱有欽佩之情的——瞎折騰什麼呢?所以,如果要講遞歸,就要一個令人信服的例子,而這個例子非漢諾塔莫屬。
漢諾塔的非遞歸解法
似乎這個問題的最佳解法就是遞歸,如果你想用棧來消解掉遞歸達到形式上的消除遞歸,你還是在使用遞歸的思想,因此,他本質上還是一個遞歸的算法。我們這本黃皮書在談論到“什麼情況使用遞歸”的時候,在“3.問題的解法是遞歸的”這裡面,就這樣說了“有些問題只能用遞歸的方法來解決,一個典型的例子就是漢諾塔”。
但我堅信,如果一個問題能用分析的辦法解決——遞歸實際上就是一個分析解法,能將問題分解成-1規模的同等問題和移動一個盤子,如果這樣分解下去一定會有解,最後分解到移動1號盤子,問題就解決了——那麼我也應該能用綜合的辦法解決,就是從當前的狀態來確定怎樣移動,而不是逆推得到決定。這是對實際工作過程的一個模擬,試想如果讓我們去搬盤子,我們肯定不會用遞歸來思考現在應該怎麼搬——只要8個盤子,我們腦子裡的“工作棧”恐怕就要溢出了——我們要立即決定怎麼搬,而不是從多少步之後的情景來知道怎麼搬。下面我們通過模擬人的正向思維來尋找這個解法。

假設如下搬7個盤子的初始狀態(選用7個是因為我曾經寫出了一個1~6結果正確的算法,而在7個的時候才發現一個條件的選擇錯誤,具體大家自己嘗試吧),我們唯一的選擇就是搬動1號盤子,但是我們的問題是向B搬還是向C搬?
顯然,我們必須將7號盤子搬到C,在這之前要把6號搬到B,5號就要搬到C,……以此類推,就會得出結論(規律1):當前柱最上面的盤子的目標柱應該是,從當前柱上“需要搬動的盤子”最下面一個的目標柱,向上交替交換目標柱到它時的目標柱。就是說,如果當前柱是A,需要移動m個盤子,從上面向下數的第m個盤子的目標柱是C,那麼最上面的盤子的目標柱就是這樣:if (m % 2) 目標和第m個盤子的目標相同(C);else 目標和第m個盤子的目標不同(B)。接下來,我們需要考慮如果發生了阻塞,該怎麼辦,如下所示:
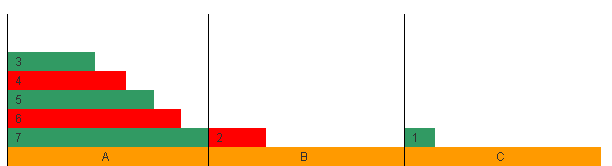
3號盤子的目標柱是C,但是已經有了1號盤子,我們最直覺的反映就是——將礙事的盤子搬到另一根柱子上面去。於是,我們要做的是(規律2):保存當前柱的信息(柱子號、應該搬動的最下面一塊盤子的號,和它的目標柱),以備當障礙清除後回到現在的柱子繼續搬,將當前柱轉換為礙事的盤子所在的柱子。假設這樣若干步後,我們將7號盤子從A搬到了C,此時,保存當前柱號的棧一定是空了,我們該怎麼辦呢?
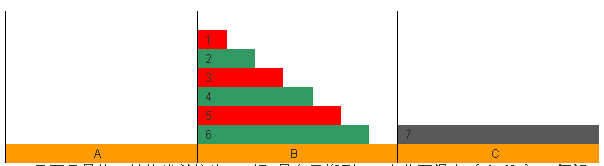
顯而易見的,轉換當前柱為B,把6號盤子搬到C。由此可得出(規律3):假設當前的問題規模為n,搬動第n個盤子到C後,問題規模減1,當前柱轉換到另一個柱子,最下面的盤子的目標柱為C。
綜上,我們已經把這個問題解決了,可以看出,關鍵是如何確定當前柱需要移動多少盤子,這個問題請大家自己考慮,給出如下例程,因為沒有經過任何優化,本人的編碼水平又比較低,所以這個函數很慢——比遞歸的還慢10倍。
#include <iostream>
#include <vector>
using namespace std;
class Needle
{
public:
Needle() { a.push_back(100); }//每一個柱子都有一個底座
void push(int n) { a.push_back(n); }
int top() { return a.back(); }
int pop() { int n = a.back(); a.pop_back(); return n; }
int movenum(int n) { int i = 1;while (a[i] > n) i++; return a.size() - i; }
int size() { return a.size(); }
int operator [] (int n) { return a[n]; }
private:
vector<int> a;
};
void Hanoi(int n)
{
Needle needle[3], ns;//3個柱子,ns是轉換柱子時的保存棧,借用了Needle的棧結構
int source = 0, target, target_m = 2, disk, m = n;
for (int i = n; i > 0; i--) needle[0].push(i);//在A柱上放n個盤子
while (n)//問題規模為n,開始搬動
{
if (!m) { source = ns.pop(); target_m = ns.pop();
m = needle[source].movenum(ns.pop()); }//障礙盤子搬走後,回到原來的當前柱
if (m % 2) target = target_m; else target = 3 - source - target_m;//規律1的實現
if (needle[source].top() < needle[target].top())//當前柱頂端盤子可以搬動時,移動盤子
{
disk = needle[source].top();m--;
cout << disk << " move " << (char)(source + 0x41) << " to "<< (char)(target + 0x41) << endl;//顯示搬動過程
needle[target].push(needle[source].pop());//在目標柱上面放盤子
if (disk == n) { source = 1 - source; target_m = 2; m = --n; }規律3的實現
}
else//規律2的實現
{
ns.push(needle[source][needle[source].size() - m]);
ns.push(target_m); ns.push(source);
m = needle[target].movenum(needle[source].top());
target_m = 3 - source - target; source = target;
}
}
}
這個算法實現比遞歸算法復雜了很多(遞歸算法在網上、書上隨便都可以找到),而且還慢很多,似乎是多余的,然而,這是有現實意義的。我不知道現在還在搬64個盤子的僧人是怎麼搬的,不過我猜想一定不是先遞歸到1個盤子,然後再搬——等遞歸出來,估計胡子一打把了(能不能在人世還兩說)。我們一定是馬上決定下一步怎麼搬,就如我上面寫的那樣,這才是人的正常思維,而用遞歸來思考,想出來怎麼搬的時候,黃瓜菜都涼了。正像我們做事的方法,雖然我今生今世完不成這項事業,但我一定要為後人完成我能完成的,而不是在那空想後人應該怎麼完成——如果達不到最終的結果,那也一定保證向正確的方向前進,而不是呆在原地空想。
由此看出,計算機編程實際上和正常的做事步驟的差距還是很大的——我們的做事步驟如果直接用計算機來實現的話,其實並不能最優,原因就是,實際中的相關性在計算機中可能並不存在——比如人腦的逆推深度是有限的,而計算機要比人腦深很多,論記憶的准確性,計算機要比人腦強很多。這也導致了一個普通的程序員和一個資深的程序員寫的算法的速度常常有天壤之別。因為,後者知道計算機喜歡怎麼思考。
迷宮
關於迷宮,有一個引人入勝的希臘神話,這也是為什麼現今每當人們提到這個問題,總是興致勃勃(對於年青人,估計是RPG玩多了),正如雖然九宮圖連小學生都能做出來,我們總是自豪的說那叫“洛書”。這個神話我不復述了,有興趣的可以在搜索引擎上輸入“希臘神話 迷宮”,就能找到很多的介紹。
迷宮的神話講述了一位英雄如何靠著“線團”殺死了牛頭怪(玩過《英雄無敵》的朋友一定知道要想造牛頭怪,就必須建迷宮,也是從這裡來的),我看到的一本編程書上援引這段神話講述迷宮算法的時候,不知是有意杜撰,還是考證不嚴,把這個過程敘述成:英雄靠著線團的幫助——在走過的路上鋪線,每到分岔口向沒鋪線的方向前進,如果遇到死胡同,沿鋪的線返回,並鋪第二條線——走進了迷宮深處,殺死了牛頭怪。然而,神話傳說講的是,英雄被當成貢品和其他的孩子送到了迷宮的深處,英雄殺死了牛頭怪,靠著線團標識的路線退出了迷宮。實際上,這個線團只是個“棧”,遠沒有現代人賦予給它的“神奇作用”。我想作者也是RPG玩多了,總想著怎樣“勇者斗惡龍”,然而,實際上卻是“勝利大逃亡”。
迷宮問題實際上是一個心理測試,它反映了測試者控制心理穩定的能力——在一次次失敗後,是否失去冷靜最終陷在迷宮之中,也正體現了一句詩,“不識廬山真面目,只緣身在此山中”。換而言之,我們研究迷宮的計算機解法,並沒有什麼意義,迷宮就是為人設計的,而不是為機器設計的,它之所以稱為“迷”宮,前提是人的記憶准確性不夠高;假設人有機器那樣的准確的記憶,只要他不傻,都能走出迷宮。現在可能有人用智能機器人的研究來反駁我,實際上,智能機器人是在更高的層面上模擬人的思考過程,只要它完全再現了人的尋路過程,它就能走出迷宮。但是,研究迷宮生成的計算機方法,卻是有意義的,因為人們總是有虐待自己的傾向(不少人在RPG裡的迷宮轉了三天三夜也不知道疲倦)。
不管怎麼說,還是親自研究一下計算機怎麼走迷宮吧。
迷宮的存儲
按照慣例,用一個二維數組來表示迷宮,0表示牆,1表示通路,以後我們的程序都走下面這個迷宮。
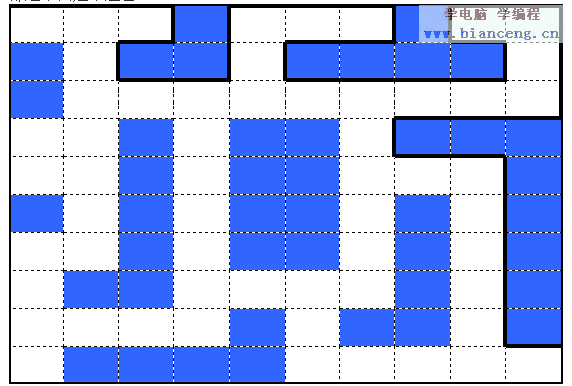
遞歸法和回溯法
有人說,回溯實際上是遞歸的展開,但實際上。兩者的指導思想並不一致。
打個比方吧,遞歸法好比是一個軍隊要通過一個迷宮,到了第一個分岔口,有3條路,將軍命令3個小隊分別去探哪條路能到出口,3個小隊沿著3條路分別前進,各自到達了路上的下一個分岔口,於是小隊長再分派人手各自去探路——只要人手足夠(對照而言,就是計算機的堆棧足夠),最後必將有人找到出口,從這人開始只要層層上報直屬領導,最後,將軍將得到一條通路。所不同的是,計算機的遞歸法是把這個並行過程串行化了。
而回溯法則是一個人走迷宮的思維模擬——他只能寄希望於自己的記憶力,如果他沒有辦法在分岔口留下標記(電視裡一演到什麼迷宮尋寶,總有惡人去改好人的標記)。
想到這裡突然有點明白為什麼都喜歡遞歸了,他能夠滿足人心最底層的虛榮——難道你不覺得使用遞歸就象那個分派士兵的將軍嗎?想想漢諾塔的解法,也有這個傾向,“你們把上面的N-1個拿走,我就能把下面的挪過去,然後你們在把那N-1個搬過來”。笑談,切勿當真。
這兩種方法的例程,我不給出了,網上很多。我只想對書上的遞歸解法發表點看法,因為書上的解法有偷梁換柱的嫌疑——迷宮的儲存不是用的二維數組,居然直接用岔路口之間的連接表示的——簡直是人為的降低了問題的難度。實際上,如果把迷宮抽象成(岔路口)點的連接,迷宮就變成了一個“圖”,求解入口到出口的路線,完全可以用圖的遍歷算法來解決,只要從入口DFS到出口就可以了;然而,從二維數組表示的迷宮轉化為圖是個很復雜的過程。並且這種轉化,實際上就是沒走迷宮之前就知道了迷宮的結構,顯然是不合理的。對此,我只能說這是為了遞歸而遞歸,然後還自己給自己開綠燈。
但迷宮並不是只能用上面的方法來走,前提是,迷宮只要走出去就可以了,不需要找出一條可能上的最短路線——確實,迷宮只是前進中的障礙,一旦走通了,沒人走第二遍。下面的方法是一位游戲玩家提出來的,既不需要遞歸,也不需要棧來回溯——玩游戲還是有收獲的。
另一種解法
請注意我在迷宮中用粗線描出的路線,實際上,在迷宮中,只要從入口始終沿著一邊的牆走,就一定能走到出口,那位玩家稱之為“靠一邊走”——如果你不把迷宮的通路看成一條線,而是一個有面積的圖形,很快你就知道為什麼。編程實現起來也很簡單。
下面的程序在TC2中編譯,不能在VC6中編譯——為了動態的表現人的移動情況,使用了gotoxy(),VC6是沒有這個函數的,而且堆砌迷宮的219號字符是不能在使用中文頁碼的操作系統的32位的console程序顯示出來的。如果要在VC6中實現gotoxy()的功能還得用API,為了一個簡單的程序沒有必要,所以,就用TC2寫了,突然換到C語言還有點不適應。
#include <stdio.h>
typedef struct hero {int x,y,face;} HERO;
void set_hero(HERO* h,int x,int y,int face){h->x=x;h->y=y;h->face=face;}
void go(HERO* h){if(h->face%2) h->x+=2-h->face;else h->y+=h->face-1;}
void goleft(HERO* h){if(h->face%2) h->y+=h->face-2;else h->x+=h->face-1;}
void turnleft(HERO* h){h->face=(h->face+3)%4;}
void turnright(HERO* h){h->face=(h->face+1)%4;}
void print_hero(HERO* h, int b)
{
gotoxy(h->x + 1, h->y + 1);
if (b)
{
switch (h->face)
{
case 0: printf("%c", 24); break;
case 1: printf("%c", 16); break;
case 2: printf("%c", 25); break;
case 3: printf("%c", 27); break;
default: break;
}
}
else printf(" ");
}
int maze[10][10] =
{
0, 0, 0, 1, 0, 0, 0, 1, 0, 0,
1, 0, 1, 1, 0, 1, 1, 1, 1, 0,
1, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 1, 0, 1, 1, 0, 1, 1, 1,
0, 0, 1, 0, 1, 1, 0, 0, 0, 1,
1, 0, 1, 0, 1, 1, 0, 1, 0, 1,
0, 0, 1, 0, 1, 1, 0, 1, 0, 1,
0, 1, 1, 0, 0, 0, 0, 1, 0, 1,
0, 0, 0, 0, 1, 0, 1, 1, 0, 1,
0, 1, 1, 1, 1, 0, 0, 0, 0, 0
};
void print_maze()
{
int i, j;
for (i = 0; i < 10; i++)
{
for (j = 0; j < 10; j++)
{
if (maze[i][j]) printf("%c", 219);
else printf(" ");
}
printf("\n");
}
}
int gomaze(HERO* h)
{
HERO t = *h; int i;
for (i = 0; i < 2; t = *h)
{
print_hero(h, 1); sleep(1); go(&t);
if (t.x >= 0 && t.x < 10 && t.y >= 0 && t.y < 10 && !maze[t.y][t.x])
{
print_hero(h, 0); go(h);/*前方可走則向前走*/
if (h->x == 9 && h->y == 9) return 1; goleft(&t);
if (h->x == 0 && h->y == 0) i++;
if (t.x >= 0 && t.x < 10 && t.y >= 0 && t.y < 10 && !maze[t.y][t.x]) turnleft(h);/*左方無牆向左轉*/
}
else turnright(h);/*前方不可走向右轉*/
}
return 0;
}
main()
{
HERO Tom;/*有個英雄叫Tom*/
set_hero(&Tom, 0, 0, 0);/*放在(0,0)面朝北*/
clrscr();
print_maze();
gomaze(&Tom);/*Tom走迷宮*/
}
總結
書上講的基本上就這些了,要是細說起來,幾天幾夜也說不完。前面我並沒有講如何寫遞歸算法,實際上給出的都是非遞歸的方法,我也覺得有點文不對題。我的目的是使大家明白,能寫出什麼算法,主要看你解決問題的指導思想,換而言之,就是對問題的認識程度。所以初學者現在就去追求“漂亮”的遞歸算法,是不現實的,結果往往就是削足適履,搞的一團糟——有位仁兄寫了個騎馬游世界的“遞歸”程序,在我機器上10分鐘沒反映。其實優秀的遞歸算法是在對問題有了清楚的認識後才會得出的。