用C++實現矩陣運算:最近學習過程中用到矩陣,這裡匯總一下用到的矩陣的各種運算。包括:求轉置矩陣(4*4);求矩陣的乘積(4*4_4*4)求逆矩陣(3*3)。
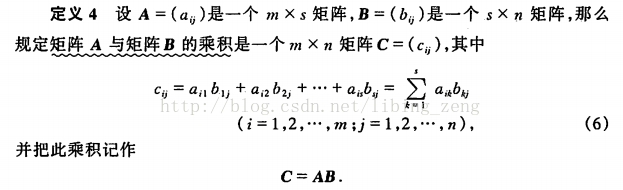
我們程序中A、B都是4*4的矩陣。
C++代碼如下:
bool matrix_4_4_multiply_4_4(const float matrix1[4][4], const float matrix2[4][4], float (&result)[4][4]) {
//求兩個4*4矩陣的乘積
for (int k=0; k<4; k++) {
for (int i=0; i<4; i++) {
result[i][k] = 0.0;
for (int j=0; j<4; j++) {
result[i][k] = result[i][k] + matrix1[i][j]*matrix2[j][k];
}
}
}
return true;
}
int main(){
float matrix1[4][4] = {{1, 2, 3, 4}, {2, 3, 4, 5}, {3, 4, 5, 6}, {4, 5, 6, 7}};
float matrix2[4][4] = {{2, 3, 4, 5}, {3, 4, 5, 6}, {4, 5, 6, 7}, {5, 6, 7, 8}};
float result[4][4];
matrix_4_4_multiply_4_4(matrix1, matrix2, result);
std::cout << "matrix1:" << endl;
for (int i=0; i<4; i++) {//打印matrix1
for (int j=0; j<4; j++) {
std::cout << matrix1[i][j] << " ";
}
std::cout << endl;
}
std::cout << endl;
std::cout << "matrix2:" << endl;
for (int i=0; i<4; i++) {//打印matrix2
for (int j=0; j<4; j++) {
std::cout << matrix2[i][j] << " ";
}
std::cout << endl;
}
std::cout << endl;
std::cout << "matrix1 multiply matrix2:" << endl;
for (int i=0; i<4; i++) {//打印matrix1和matrix2的乘積
for (int j=0; j<4; j++) {
std::cout << result[i][j] << " ";
}
std::cout << endl;
}
}
輸出結果如下:
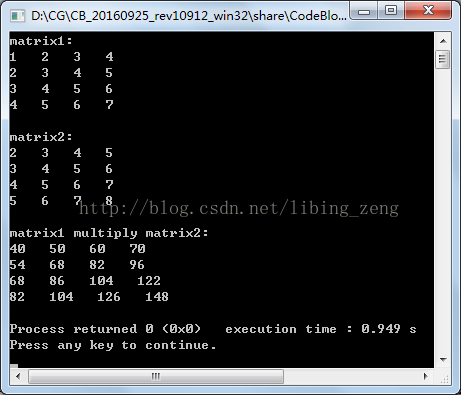

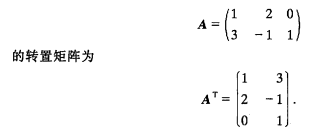
我們程序中用到的4*4的矩陣的轉置。
C++代碼如下:
bool get_matrix_transpose_4_4(const float matrix[4][4], float (&result)[4][4]) {
for (int i=0; i<4; i++) {
for (int j=0; j<4; j++) {
result[j][i] = matrix[i][j];
}
}
return true;
}
int main(){
float matrix3[4][4] = {{1, 2, 3, 4}, {3, 4, 5, 6}, {5, 6, 7, 8}, {7, 8, 9, 0}};
float transpose[4][4];
get_matrix_transpose_4_4(matrix3, transpose);
std::cout << "matrix3:" << endl;
for (int i=0; i<4; i++) {
for (int j=0; j<4; j++) {
std::cout << matrix3[i][j] << " ";
}
std::cout << endl;
}
std::cout << endl;
std::cout << "transpose:" << endl;
for (int i=0; i<4; i++) {
for (int j=0; j<4; j++) {
std::cout << transpose[i][j] << " ";
}
std::cout << endl;
}
}
輸出結果如下:
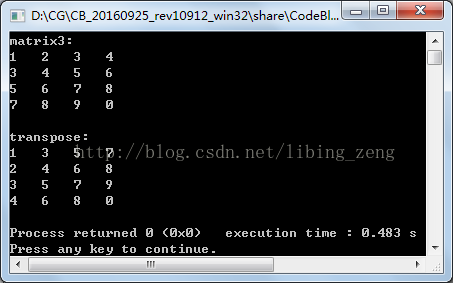
求逆矩陣可以用伴隨矩陣,也可以用初等變換。我們這裡是用伴隨矩陣的方法來求逆矩陣。
代數余子式:

伴隨矩陣:

行列式的計算:
(因為我們這裡用到的是3*3的矩陣,所以,這裡只考慮3階行列式)

求逆矩陣:


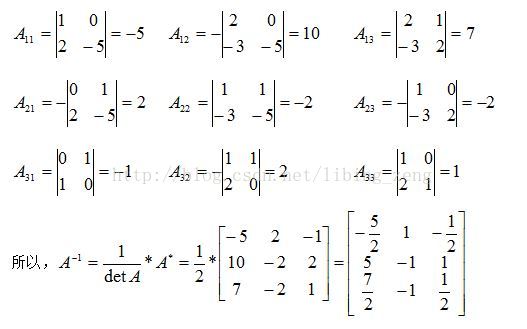
C++代碼如下:
bool get_matrix_inverse_3_3(const float m[3][3], float (&inverse)[3][3]) {
float det_m = m[0][0]*m[1][1]*m[2][2] + m[0][1]*m[1][2]*m[2][0] + m[0][2]*m[1][0]*m[2][1] -
m[0][2]*m[1][1]*m[2][0] - m[0][0]*m[1][2]*m[2][1] - m[0][1]*m[1][0]*m[2][2];
if (fabs(det_m) < 1e-6) {
return false;
}
else {
vec3 a = (1/det_m)*vec3(m[1][1]*m[2][2] - m[1][2]*m[2][1],
m[1][2]*m[2][0] - m[1][0]*m[2][2],
m[1][0]*m[2][1] - m[1][1]*m[2][0]);
vec3 b = (1/det_m)*vec3(m[0][2]*m[2][1] - m[0][1]*m[2][2],
m[0][0]*m[2][2] - m[0][2]*m[2][0],
m[0][1]*m[2][0] - m[0][0]*m[2][1]);
vec3 c = (1/det_m)*vec3(m[0][1]*m[1][2] - m[0][2]*m[1][1],
m[0][2]*m[1][0] - m[0][0]*m[1][2],
m[0][0]*m[1][1] - m[0][1]*m[1][0]);
get_matrix_3_3(a, b, c, inverse);
return true;
}
}
int main(){
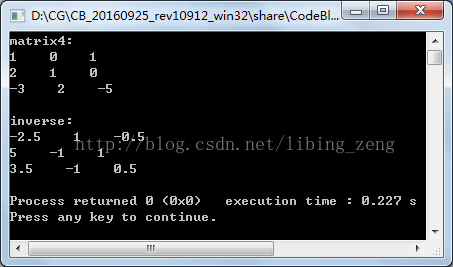
float matrix4[3][3] = {{1, 0, 1}, {2, 1, 0}, {-3, 2, -5}};
float inverse[3][3];
get_matrix_inverse_3_3(matrix4, inverse);
std::cout << "matrix4:" << endl;
for (int i=0; i<3; i++) {
for (int j=0; j<3; j++) {
std::cout << matrix4[i][j] << " ";
}
std::cout << endl;
}
std::cout << endl;
std::cout << "inverse:" << endl;
for (int i=0; i<3; i++) {
for (int j=0; j<3; j++) {
std::cout << inverse[i][j] << " ";
}
std::cout << endl;
}
}
輸出結果如下: