算法詳解之分支限界法的詳細完成。本站提示廣大學習愛好者:(算法詳解之分支限界法的詳細完成)文章只能為提供參考,不一定能成為您想要的結果。以下是算法詳解之分支限界法的詳細完成正文
起首我們來存眷一個成績:
成績描寫:
布線成績:印刷電路板將布線區域劃分紅n×m個方格陣列,請求肯定銜接方格陣列中的方格a的中點到方格b的中點的最短布線計劃。在布線時,電路只能沿直線或直角布線,為了不線路訂交,已布了線的方格做了封閉標志,其他線路不許可穿過被封閉的方格。以下圖所示:
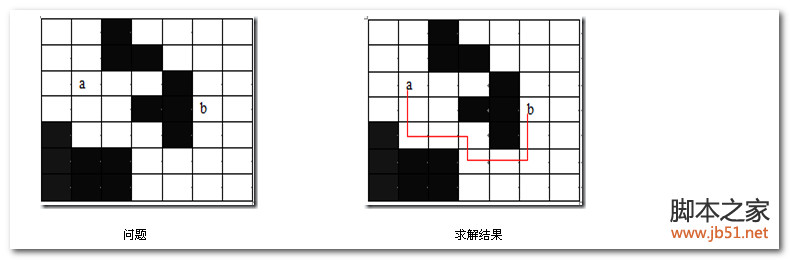
算法思緒:
布線成績的解空間是一個圖,則從肇端地位a開端將它作為第一個擴大結點。與該擴大結點相鄰並可達的方格成為可行結點被參加到活扣點隊列中,而且將這些方格標志為1,即從肇端方格a到這些方格的間隔為1。接著,從活扣點隊列中掏出隊首結點作為下一個擴大結點,並將與以後擴大結點相鄰且未標志過的方格標志為2,並存入活扣點隊列。這個進程一向持續到算法搜刮到目的方格b或活扣點隊列為空時為止。
在完成上述算法時,
(1) 界說一個表現電路板上方格地位的類Position。
它的2個成員row和col分離表現方格地點的行和列。在方格處,布線可沿右、下、左、上4個偏向停止。沿這4個偏向的挪動分離記為0,1,2,3。下表中,offset[i].row和offset[i].col(i= 0,1,2,3)分離給出沿這4個偏向進步1步絕對於以後方格的絕對位移。

(2) 用二維數組grid表現所給的方格陣列。
初始時,grid[i][j] = 0, 表現該方格許可布線,而grid[i][j] = 1表現該方格被封閉,不許可布線。
算法圖解:
代碼貼出來:
#include <stdio.h>
typedef struct {
int row;
int col;
}Position;
int FindPath (Position start, Position finish, int &PathLen, Position *&path)
{ //盤算從肇端地位start到目的地位finish的最短布線途徑,找到前往1,不然,前往0
int i;
if ((start.row = = finish.row) && (start.col = = finish.col)) {
PathLen = 0; return 0; } //start = finish
//設置方格陣列”圍牆”
for (i = 0; i <= m+1; i++)
grid[0][i] = grid[n+1][i] = 1; //頂部和底部
for (i = 0; i <= n+1; i++)
grid[i][0] = grid[i][m+1] = 1; //右翼和左翼
//初始化絕對位移
int NumOfNbrs = 4; //相鄰方格數
Position offset[4], here, nbr;
offset[0].row = 0; offset[0].col = 1; //右
offset[0].row = 1; offset[0].col = 0; //下
offset[0].row = 0; offset[0].col = -1; //左
offset[0].row = -1; offset[0].row = 0; //上
here.row = start.row;
here.col = start.col;
LinkedQueue <Position> Q; //標志可達方格地位
do {
for (i = 0; i< NumOfNbrs; i++) { //標志可達相鄰方格
nbr.row = here.row + offset[i].row ;
nbr.col = here.col + offset[i].col;
if (grid[nbr.row][nbr.col] = = 0) { //該方格未標志
grid[nbr.row][nbr.col] = grid[here.row][here.col] + 1;
if ((nbr.row = = finish.row) && (nbr.col = = finish.col)) break;//完成布線
Q.Add(nbr);
}
}
if ((nbr.row = = finishi.row) && (nbr.col = = finish.col)) break;//完成布線
if (Q.IsEmpty()) //活隊列能否為空
return 0; //無解
Q.delete(here); //取下一個擴大結點
}while (1);
//結構最短布線途徑
PathLen = grid[finish.row][finish.col] - 2;
path = new Position[PathLen];
here = finish;
for (int j = PathLen – 1; j >= 0; j--) { //找先驅地位
path[j] = here;
for (i = 0; i< NumOfNbrs; i++) {
nbr.row = here.row + offset[i].row ;
nbr.col = here.col + offset[i].col;
if (grid[nbr.row][nbr.col] = = j+2) break;
}
here = nbr; //向前挪動
}
return 1;
}
void main ()
{
int grid[8][8];
int PathLen, *path;
Position start, finish;
start.row = 3; start.col = 2;
finish.row = 4; finish.col = 6;
FindPath (start, finish, PathLen, path);
}
代碼貼出來:
#include <stdio.h>
typedef struct {
int row;
int col;
}Position;
int FindPath (Position start, Position finish, int &PathLen, Position *&path)
{ //盤算從肇端地位start到目的地位finish的最短布線途徑,找到前往1,不然,前往0
int i;
if ((start.row = = finish.row) && (start.col = = finish.col)) {
PathLen = 0; return 0; } //start = finish
//設置方格陣列”圍牆”
for (i = 0; i <= m+1; i++)
grid[0][i] = grid[n+1][i] = 1; //頂部和底部
for (i = 0; i <= n+1; i++)
grid[i][0] = grid[i][m+1] = 1; //右翼和左翼
//初始化絕對位移
int NumOfNbrs = 4; //相鄰方格數
Position offset[4], here, nbr;
offset[0].row = 0; offset[0].col = 1; //右
offset[0].row = 1; offset[0].col = 0; //下
offset[0].row = 0; offset[0].col = -1; //左
offset[0].row = -1; offset[0].row = 0; //上
here.row = start.row;
here.col = start.col;
LinkedQueue <Position> Q; //標志可達方格地位
do {
for (i = 0; i< NumOfNbrs; i++) { //標志可達相鄰方格
nbr.row = here.row + offset[i].row ;
nbr.col = here.col + offset[i].col;
if (grid[nbr.row][nbr.col] = = 0) { //該方格未標志
grid[nbr.row][nbr.col] = grid[here.row][here.col] + 1;
if ((nbr.row = = finish.row) && (nbr.col = = finish.col)) break;//完成布線
Q.Add(nbr);
}
}
if ((nbr.row = = finishi.row) && (nbr.col = = finish.col)) break;//完成布線
if (Q.IsEmpty()) //活隊列能否為空
return 0; //無解
Q.delete(here); //取下一個擴大結點
}while (1);
//結構最短布線途徑
PathLen = grid[finish.row][finish.col] - 2;
path = new Position[PathLen];
here = finish;
for (int j = PathLen – 1; j >= 0; j--) { //找先驅地位
path[j] = here;
for (i = 0; i< NumOfNbrs; i++) {
nbr.row = here.row + offset[i].row ;
nbr.col = here.col + offset[i].col;
if (grid[nbr.row][nbr.col] = = j+2) break;
}
here = nbr; //向前挪動
}
return 1;
}
void main ()
{
int grid[8][8];
int PathLen, *path;
Position start, finish;
start.row = 3; start.col = 2;
finish.row = 4; finish.col = 6;
FindPath (start, finish, PathLen, path);
}
好了,成績解出來了。咦,我們用的是甚麼辦法呢?呵呵,對,這就是分支限界算法。
算法總結:
分支限界法根本思惟:
• 分支限界法常以廣度優先或以最小消耗(最年夜效益)優先的方法搜刮成績的解空間樹。
• 在分支限界法中,每個活扣點只要一次機遇成為擴大結點。活扣點一旦成為擴大結點,就一次性發生其一切兒子結點。
• 在這些兒子結點中,招致弗成行解或招致非最優解的兒子結點被捨棄,其他兒子結點被參加活扣點表中。
• 爾後,從活扣點表中取下一結點成為以後擴大結點,偏重復上述結點擴大進程。這個進程一向連續到找到所需的解或活扣點表為空時為止。
分支限界法與回溯法的分歧:
(1)求解目的分歧:回溯法的求解目的是找出解空間樹中知足束縛前提的一切解,而分支限界法的求解目的則是找出知足束縛前提的一個解,或是在知足束縛前提的解中找出在某種意義下的最優解。
(2)搜刮方法的分歧:回溯法以深度優先的方法搜刮解空間樹,而分支限界軌則以廣度優先或以最小消耗優先的方法搜刮解空間樹。