算法詳解之分治法詳細完成。本站提示廣大學習愛好者:(算法詳解之分治法詳細完成)文章只能為提供參考,不一定能成為您想要的結果。以下是算法詳解之分治法詳細完成正文
分治算法的根本思惟是將一個范圍為N的成績分化為K個范圍較小的子成績,這些子成績互相自力且與原成績性質雷同。求出子成績的解,便可獲得原成績的解。
分治法解題的普通步調:
(1)分化,將要處理的成績劃分紅若干范圍較小的同類成績;
(2)求解,當子成績劃分得足夠小時,用較簡略的辦法處理;
(3)歸並,按原成績的請求,將子成績的解逐層歸並組成原成績的解。
一言以蔽之:分治法的設計思惟是,將一個難以直接處理的年夜成績,朋分成一些范圍較小的雷同成績,以便各個擊破,分而治之。
在熟悉分治之前很有需要先懂得一下遞歸,固然,遞歸也是最根本的編程成績,普通接觸過編程的人都邑對遞歸有一些熟悉.為何要先懂得遞歸呢?你看,依據下面所說的,我們就要將一個成績分紅若干個小成績,然後逐個求解而且最初歸並,這就是一個遞歸的成績,遞歸的去分化本身,遞歸的去處理每個小成績,然後歸並…
關於遞歸,這裡舉一個最簡略的例子,求N!;
我們只須要界說函數
int calculate(int n)
{
if(n==1)
return 1;
else
return n*calculate(n-1); //挪用本身…
}
好了,有了遞歸的鋪墊,我們上去來看一看一個分治算法的成績,合並排序成績…
根本思惟:
將待排序元素分紅年夜小年夜致雷同的2個子聚集(遞歸直到最小的排序單位),分離對2個子聚集停止排序,終究將排好序的子聚集歸並成為所請求的排好序的聚集。
上面我們用一張圖來展現全部流程,最上面的(權且叫他第一層)是原始數組分紅了8個最小排序成績,各自只要一個元素,故不須要排序,年夜家可以看到,我們經由過程分而治之的思惟把對最後數組的排序分為了若干個只要一個元素的小數組的排序,然後第二層,我們停止了歸並,將每兩個最小排序成果歸並為有兩個元素的數組,然後逐層往長進行歸並,就有了最初的成果…

上面我們來看一下這個算法的詳細完成,上面的MERGE-SORT (A, p, r)表現對數組A[p->r]的排序進程.個中p->r代表從p到r.
MERGE-SORT (A, p, r)
1. IF p < r // 停止A[p->r]的排序進程天然須要p<r的條件前提
2. THEN q = [(p + r)/2] // 將以後的排序成績一分為二,分離停止處置
3. MERGE-SORT (A, p, q) //持續遞歸看能不克不及將成績持續一分為二,處置A[p->q]的排序
4. MERGE-SORT (A, q + 1, r) // 持續遞歸看能不克不及將成績持續一分為二處置A[q+1->r]的排序
5. MERGE (A, p, q, r) // 歸並以後成果
到這裡,分治算法的精華曾經出來了,我們經由過程遞歸將成績停止分化到足夠小…繼而停止成果盤算…然後再將成果歸並.
上面來處置一下邊角料的任務,呵呵,讓年夜家看到一個完全的合並排序的例子,全部算法總結系列我都沒有很好的應用偽代碼,而是應用我以為普遍應用的C說話代碼來停止代碼诠釋.現實上,描寫算法最好照樣應用偽代碼比擬好,這裡我對我後面的四篇文章沒有應用偽代碼而小小的小看一下本身,太不專業了..呵呵
以下算法MERGE (A, p, q, r )表現歸並A[p->q]和A[q+1->r]這兩個曾經排序好的數組
MERGE (A, p, q, r )
1. n1 ← q − p + 1 //盤算A[p->q]的長度
2. n2 ← r − q //盤算A[q+1->r]的長度
3. Create arrays L[1 . . n1 + 1] and R[1 . . n2 + 1] //創立兩個數組
4. FOR i ← 1 TO n1
5. DO L[i] ← A[p + i − 1]
6. FOR j ← 1 TO n2
7. DO R[j] ← A[q + j ] //4-7行是將原數組中A[p->r]的元素掏出到新創立的數組,我們的操作是基於暫時數組的操作
8. L[n1 + 1] ← ∞
9. R[n2 + 1] ← ∞ //8-9行設置界線..
10. i ← 1
11. j ← 1
12. FOR k ← p TO r
13. DO IF L[i ] ≤ R[ j]
14. THEN A[k] ← L[i]
15. i ← i + 1
16. ELSE A[k] ← R[j]
17. j ← j + 1 //12-17行停止排序合
這裡我照樣供給一個詳細的完成,請見上面的代碼
C說話代碼
關於代碼正文,請見博客下面的偽代碼正文..
#include<stdio.h>
int L[100],R[100];
void merge(int numbers[],int left, int mid, int right)
{
int n1=mid-left+1;
int n2=right-mid;
int i,j,k;
for(i=1;i<=n1;i++)
L[i]=numbers[left+i-1];
for( j=1;j<=n2;j++)
R[j]=numbers[mid+j];
L[n1+1]=99999;
R[n2+1]=99999;
i=1;
j=1;
for(k=left;k<=right;k++)
if(L[i]<=R[j])
{
numbers[k]=L[i];
i++;
}
else
{
numbers[k]=R[j];
j++;
}
}
void mergeSort(int numbers[],int left, int right)
{
if(left<right)
{
int mid;
mid = (right + left) / 2;
mergeSort(numbers, left, mid);
mergeSort(numbers, mid+1, right);
merge(numbers,left, mid, right);
}
}
int main()
{
int numbers[]={5,2,4,6,1,3,2,6};
mergeSort(numbers,0,7);
for(int i=0;i<8;i++)
printf("%d",numbers[i]);
}
合並排序算法的時光龐雜度是O(nlogn),關於冒泡排序的O(n*n),效力還有有比擬好的進步..
其實自己本來在進修的時刻好長一段時光不睬解為何時光龐雜度會是O(nlogn),像冒泡排序就比擬好懂得,有兩個for輪回,成績的范圍跟著n變年夜而變年夜,算法時光龐雜度天然就是O(n*n),前面花了一些時光來浏覽一些材料才明確其道理,這裡我曾經將材料地址放到了本文最初,有興致的也能夠去看看.簡略的描寫一下為何會是O(nlogn)
年夜家看看,我們的例子,解一個8個元素的數組,我們用到了幾層?是四層,假定我們這裡有n個元素,我們會用到若干層?依據必定的歸結總結,我們曉得我們會用到(lgn)+1層..(lgn)+1層須要用到lgn條理的歸並算法.如今再看看MERGE (A, p, q, r )的龐雜度是若干,毫無疑問O(n),故其合並排序的算法時光龐雜度是O(nlogn).固然這個成果還可以經由過程其他的辦法盤算出來,我這裡是白話話最簡練的一種..
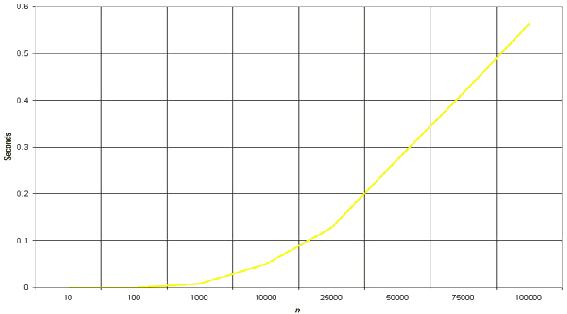
上面來一張算法時光龐雜度的與n范圍的關系圖..