C++實現二叉查找樹

在數據結構中，有一個奇葩的東西，說它奇葩，那是因為它重要，這就是樹。而在樹中，二叉樹又是當中的貴族。二叉樹的一個重要應用是它們在查找中的應用，於是就有了二叉查找樹。 使二叉樹成為一顆二叉查找樹，需要滿足以下兩點：

1. 對於樹中的每個節點X，它的左子樹中所有項的值都要小於X中的項；
2. 對於樹中的每個節點Y，它的右子樹中所有項的值都要大於Y中的項。

二叉查找樹的基本操作

以下是對於二叉查找樹的基本操作定義類，然後慢慢分析是如何實現它們的。

template<class T>class BinarySearchTree{public:
    // 構造函數，初始化root值
    BinarySearchTree() : root(NULL){}

    // 析構函數，默認實現
    ~BinarySearchTree() {}

    // 查找最小值，並返回最小值
    const T &findMin() const;

    // 查找最大值，並返回最大值
    const T &findMax() const;

    // 判斷二叉樹中是否包含指定值的元素
    bool contains(const T &x) const;

    // 判斷二叉查找樹是否為空
    bool isEmpty() const { return root ? false : true; }

    // 打印二叉查找樹的值
    void printTree() const;

    // 向二叉查找樹中插入指定值
    void insert(const T &x);

    // 刪除二叉查找樹中指定的值
    void remove(const T &x);

    // 清空整個二叉查找樹
    void makeEmpty() const;private:
    // 指向根節點
    BinaryNode<T> *root;

    void insert(const T &x, BinaryNode<T> *&t) const;
    void remove(const T &x, BinaryNode<T> *&t) const;
    BinaryNode<T> *findMin(BinaryNode<T> *t) const;
    BinaryNode<T> *findMax(BinaryNode<T> *t) const;
    bool contains(const T &x, BinaryNode<T> *t) const;
    void printTree(BinaryNode<T> *t) const;
    void makeEmpty(BinaryNode<T> *&t) const;};

findMin和findMax實現

根據二叉查找樹的性質：

1. 對於樹中的每個節點X，它的左子樹中所有項的值都要小於X中的項；
2. 對於樹中的每個節點Y，它的右子樹中所有項的值都要大於Y中的項。

我們可以從root節點開始：

1. 一直沿著左節點往下找，直到子節點等於NULL為止，這樣就可以找到最小值了；
2. 一直沿著右節點往下找，直到子節點等於NULL為止，這樣就可以找到最大值了。

如下圖所示：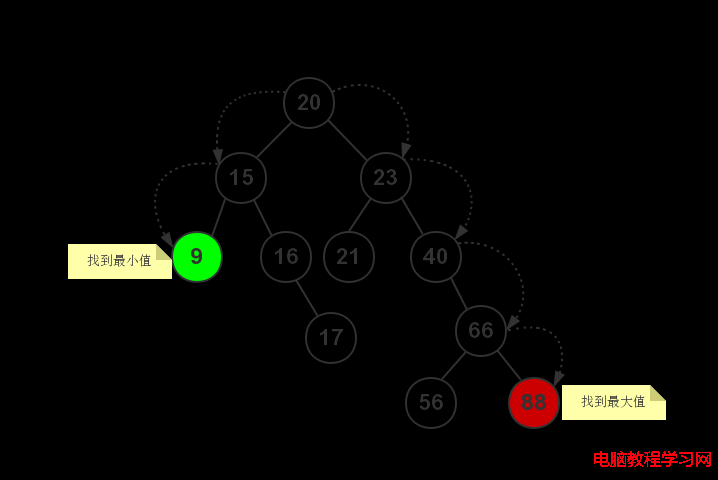 

在程序中實現時，有兩種方法：

1. 使用遞歸實現；
2. 使用非遞歸的方式實現。

對於finMin的實現，我這裡使用遞歸的方式，代碼參考如下：

BinaryNode<T> *BinarySearchTree<T>::findMin(BinaryNode<T> *t) const{
    if (t == NULL)
    {
        return NULL;
    }
    else if (t->left == NULL)
    {
        return t;
    }
    else
    {
        return findMin(t->left);
    }}

在findMin()的內部調用findMin(BinaryNode<T> *t)，這樣就防止了客戶端知道了root根節點的信息。上面使用遞歸的方式實現了查找最小值，下面使用循環的方式來實現findMax。

template<class T>BinaryNode<T> *BinarySearchTree<T>::findMax(BinaryNode<T> *t) const{
    if (t == NULL)
    {
        return NULL;
    }

    while (t->right)
    {
        t = t->right;
    }
    return t;}

在很多面試的場合下，面試官一般都是讓寫出非遞歸的版本；而在對樹進行的各種操作，很多時候都是使用的遞歸實現的，所以，在平時學習時，在理解遞歸版本的前提下，需要關心一下對應的非遞歸版本。

contains實現

contains用來判斷二叉查找樹是否包含指定的元素。代碼實現如下：

template<class T>bool BinarySearchTree<T>::contains(const T &x, BinaryNode<T> *t) const{
    if (t == NULL)
    {
        return false;
    }
    else if (x > t->element)
    {
        return contains(x, t->right);
    }
    else if (x < t->element)
    {
        return contains(x, t->left);
    }
    else
    {
        return true;
    }}

算法規則如下：

1. 首先判斷需要查找的值與當前節點值的大小關系；
2. 當小於當前節點值時，就在左節點中繼續查找；
3. 當大於當前節點值時，就在右節點中繼續查找；
4. 當找到該值時，直接返回true。

insert實現

insert函數用來向二叉查找樹中插入新的元素，算法處理如下：

1. 首先判斷需要插入的值與當前節點值得大小關系；
2. 當小於當前節點值時，就在左節點中繼續查找插入點；
3. 當大於當前節點值時，就在右節點中繼續查找插入點；
4. 當等於當前節點值時，什麼也不干。

代碼實現如下：

template<class T>void BinarySearchTree<T>::insert(const T &x, BinaryNode<T> *&t) const{
    if (t == NULL)
    {
        t = new BinaryNode<T>(x, NULL, NULL);
    }
    else if (x < t->element)
    {
        insert(x, t->left);
    }
    else if (x > t->element)
    {
        insert(x, t->right);
    }}

remove實現

remove函數用來刪除二叉查找樹中指定的元素值，這個處理起來比較麻煩。在刪除子節點時，需要分以下幾種情況進行考慮（結合下圖進行說明）： 如下圖所示： 

1. 需要刪除的子節點，它沒有任何子節點；例如圖中的節點9、節點17、節點21、節點56和節點88；這些節點它們都沒有子節點；
2. 需要刪除的子節點，只有一個子節點（只有左子節點或右子節點）；例如圖中的節點16和節點40；這些節點它們都只有一個子節點；
3. 需要刪除的子節點，同時擁有兩個子節點；例如圖中的節點66等。

對於情況1，直接刪除對應的節點即可；實現起來時比較簡單的；

對於情況2，直接刪除對應的節點，然後用其子節點占據刪除掉的位置；

對於情況3，是比較復雜的。首先在需要被刪除節點的右子樹中找到最小值節點，然後使用該最小值替換需要刪除節點的值，然後在右子樹中刪除該最小值節點。
假如現在需要刪除包含值23的節點，步驟如下圖所示：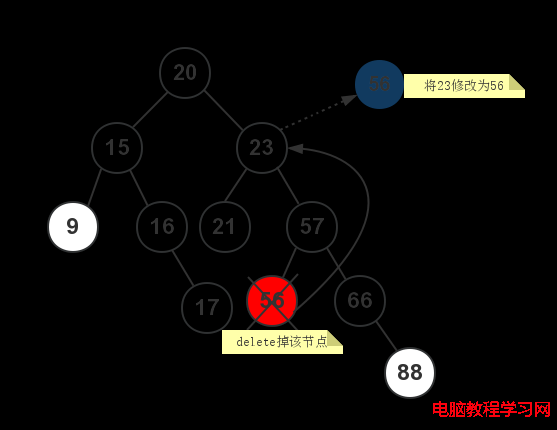 

代碼實現如下：

template<class T>void BinarySearchTree<T>::remove(const T &x, BinaryNode<T> *&t) const{
    if (t == NULL)
    {
        return;
    }

    if (x < t->element)
    {
        remove(x, t->left);
    }
    else if (x > t->element)
    {
        remove(x, t->right);
    }
    else if (t->left != NULL && t->right != NULL)
    {
        // 擁有兩個子節點
        t->element = findMin(t->right)->element;
        remove(t->element, t->right);
    }
    else if (t->left == NULL && t->right == NULL)
    {
        // 沒有子節點，直接干掉
        delete t;
        t = NULL;
    }
    else if (t->left == NULL || t->right == NULL)
    {
        // 擁有一個子節點
        BinaryNode *pTemp = t;
        t = (t->left != NULL) ? t->left : t->right;
        delete pTemp;
    }}   

makeEmpty實現

makeEmpty函數用來釋放整個二叉查找樹占用的內存空間，同理，也是使用的遞歸的方式來實現的。具體代碼請下載文中最後提供的源碼。

總結

這篇文章對數據結構中非常重要的二叉查找樹進行了詳細的總結，雖然二叉查找樹非常重要，但是理解起來還是非常容易的，主要是需要掌握對遞歸的理解。如果對遞歸有非常扎實的理解，那麼對於樹的一些操作，那都是非常好把握的，而理解二叉查找樹又是後續的AVL平衡樹和紅黑樹的基礎，希望這篇文章對大家有幫助