C語言循環控制程序舉例

【例6.10】用下面的公式求π：


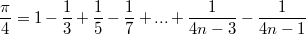
分析：首先，系數為正數的項的分母是4n-3(n為正數項的項數)，為負數的項的分母為4n-1(n為負數項的項數)，即分母的變化規律是1、3、5、7...的奇數數列，則第n項的分母為2n-1，第10000項的分母為2*10000-1。
 

#include <stdio.h>
#include <math.h>
int main(void)
{
    double p=0,j=1;
    int i;
    for( i=1;i<10000;i++ )  //此處i為項數
    {
        j=pow(-1.0,i+1)/(2*i-1);  //pow(x,y)求x的y次冪
        p+=j;
        printf("%lf\n",4*p);  //輸出每一項的值
    }
    printf("%lf\n",4*p);  //輸出最終pi值
    return 0;
}

i 的值越大，結果越精准，同樣計算時間也更長。

注意：經讀者反饋，筆者意識到以前提供的例子是錯的，上面是更改後的代碼，更改時間為 2014-07-06  1:50:34；錯誤的例子就不提供了。

【例6-11】判斷m是否素數。

#include <stdio.h>
#include <math.h>
int main(void){
    int m,i,k;
    printf("Input your number: ");
    scanf("%d",&m);
    k=sqrt(m);  // m 的開方
    for(i=2;i<=k;i++)
        if(m%i==0) break;
    if(i>=k+1)
        printf("%d is a prime number\n",m);
    else
        printf("%d is not a prime number\n",m);
    return 0;
}

【例6-12】求100至200間的全部素數。

#include <stdio.h>
#include <math.h>
int main(void){
    int m,i,k,n=0;
    for(m=101;m<=200;m=m+2){
        k=sqrt(m);  // m 的開方
        for(i=2;i<=k;i++)
            if(m%i==0)  break;
        if(i>=k+1){
            printf("%d\n",m);
            n=n+1;
        }
    }
    printf("\n");
    return 0;
}

注意：經讀者 @ahlei、@婁 @IKGROADS、@啊啊、@hi、@小姐” 的反饋，筆者意識到以前提供的例子讓人費解，將代碼做了修改，就是上面的代碼，修改時間為 2014-07-06  02:05:251。

下面是老代碼：

#include<math.h>
main(){
    int m,i,k,n=0;
    for(m=101;m<=200;m=m+2){
        k=sqrt(m);
        for(i=2;i<=k;i++)
            if(m%i==0)  break;
        if(i>=k+1){
            printf("%d",m);
            n=n+1;
        }
        if(n%n==0)printf("\n");
    }
    printf("\n");
}