Longest Valid Parentheses，longestparentheses

Longest Valid Parentheses，longestparentheses

Given a string containing just the characters '(' and ')', find the length of the longest valid (well-formed) parentheses substring.

For "(()", the longest valid parentheses substring is "()", which has length = 2.

Another example is ")()())", where the longest valid parentheses substring is "()()", which has length = 4.

問題描述：給定一個只包含“（”和")"的串，找出一個最長的符合規則的子串。

對於“（（）”，最長有效子串是“（）”，所以長度是2

另一個例子，“）（）（））”，最長的有效字串是“（）（）”，所以長度是4.

　　解題思路：

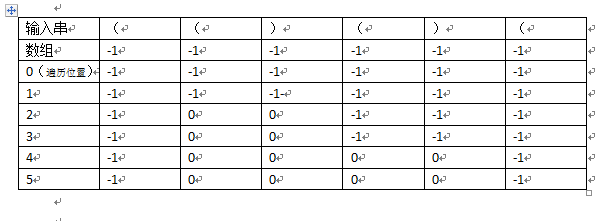
　　（1）申請一個與輸入串長度相同的整型數組，初始化值全部為-1，數組和輸入串有一一對應的關系；

　　（2）遍歷輸入串遇到“（”，就將其對應位置下標入棧；

　　（3）遇到“）”，就將數組對應位置的值設置為0，彈出棧中第一個值，並將整型數組對應位置置0，這樣保證對應的“（）”，它們在整型數組中對應的值是0；

　　（4）遍歷結束，尋找0的連續個數最大值，就是要求的結果。

int longestValidParentheses(char* s) {
    int slen=strlen(s);
    if(slen<=1)return 0;
    
      int* index=(int*)malloc(sizeof(int)*slen);
      
      for(int i=0;i<slen;i++)index[i]=-1;
      
      int* stack=(int*)malloc(sizeof(int)*slen);
      int top=0;
      
      for(int i=0;i<slen;i++)
          if(s[i]=='(')stack[top++]=i;
          else{
              if(top!=0){
                  index[stack[top-1]]=0;
                  index[i]=0;
                  top--;
              }
          }
          
    int count=0;
    int newCount=0;
    for(int i=0;i<slen;i++)
        if(index[i]!=-1)newCount++;
        else{
            if(newCount>count){
                count=newCount;
                
            }
            newCount=0;
        }
    if(newCount>count)count=newCount;
    return count;
}