數據結構:二叉樹的鏈式存儲(C語言版)
1.寫在前面
二叉樹同樣有兩種存儲方式,數組和鏈式存儲,對於數組來說,我們利用二叉樹的性質然後利用下標可以方便的找到一個節點的子節點和父節點。
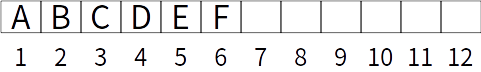
二叉樹的性質:
1.二叉樹的第i層上至多有2i-1個節點
2.深度為K的二叉樹至多有2k-1個節點
3.任何一個二叉樹中度數為2的節點的個數必度數為0的節點數目少1.
說明:度數為0,為葉子節點。
4.具有n個節點的完全二叉樹的深度為|_Log2N_|+1
5.若完全二叉樹中的某節點編號為i,則若有左孩子編號為2i,若有右孩子編號為2i+1,母親節點為i/2。
結合第5條性質,可以在這種完全二叉樹中十分方便的找到任何相關聯(父子、兄弟等)的元素。
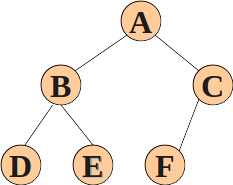
但是由於順序存儲天生適配於完全二叉樹,對於下面這種非完全二叉樹並不合適,所以我們需要用到另一種存儲方式——鏈式存儲。
在鏈式存儲中,每個節點的結構如下
一個存儲數據的變量與兩個指向孩子的指針域。
利用指針域我們便可以完美的存儲非完全二叉樹,如下:
2.代碼分解
►首先根據上述圖示,我們不難給出節點的描述
typedef struct BiTNode
{
TElemType data;
struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;
►創建和遍歷鏈式二叉樹
創建二叉樹並不是十分容易的,因為它的創建方式也對應三種順序,其實我認為二叉樹的遍歷和二叉樹的創建可以說是幾乎一樣的過程。無非是創建的過程是給data賦值,遍歷是取出data。
我們先不給出創建的代碼,而是要明白:
說明:
1.葉子節點不是沒有左右孩子,只不過左右孩子都是空。
2.我們在手動創建的過程中要根據層數來判斷葉子節點左右空孩子的個數!
3.創建和遍歷的執行順序是一樣的,那麼輸入和取出的值才會是一樣的。
比如我們要先序創建一個上述圖片中的二叉樹,我們應該怎樣輸入呢?
AB##CD##EF##G##
# 在這裡是表示葉子節點的左右節點為空。
代碼如下:
void createBitree(Bitree &T)
{
char ch;
if((ch=getchar())=='#')
T=NULL;
else
{
T=(Bitnode*)malloc(sizeof(Bitnode));
T->data=ch;
createBitree(T->Lchild);
createBitree(T->Rchild);
}
}
►遍歷代碼和創建代碼基本一樣:
/*先序遍歷*/
void preTraverse(Bitree T)
{
if(T!=NULL)
{
printf("%c",T->data);
preTraverse(T->Lchild);
preTraverse(T->Rchild);
}
}
/*中序遍歷*/
void inorder(Bitree T)
{
if(T!=NULL)
{
inorder(T->Lchild);
printf("%c",T->data);
inorder(T->Rchild);
}
}
/*後序遍歷*/
void postorder(Bitree T)
{
if(T!=NULL)
{
postorder(T->lchild);
postorder(T->rchild);
printf("%c",T->data);
}
}
►我們輸入字符後三種遍歷情況如下:
AB##CD##EF##G##
ABCDEFG
BADCFEG
BDFGECA
►求二叉樹的深度
int Depth(Bitree T)
{//返回深度
int d,dl,dr;
if(!T)
d=0;
else {
dl=Depth(T->Lchild);
dr=Depth(T->Rchild);
d=1+(dl>dr?dl:dr) ;
}
return d;
}
►二叉樹的層序遍歷
queue<Bitree> TreeQueue; //使用隊列
TreeQueue.push(tree); //先將隊頭元素加入隊列
Bitree p = tree;
while (!TreeQueue.empty()) //循環判斷隊列是否未空,若不空則
{
p = TreeQueue.front(); //獲取隊列頭節點,並出隊列
TreeQueue.pop();
printf(" %c ", p->data); //打印隊列元素
if (p->Lchild) //如果該節點有左節點
{
TreeQueue.push(p->Lchild); //加入隊列
}
if (p->Rchild) //如果該節點有右節點
{
TreeQueue.push(p->Rchild); //加入隊列
}
}
|說明:
1.算法軌跡:
依舊使用下圖:
演示:
我們首先將A加入隊列, 此時對列 中只有 ⇐[A]
我們將A出彈出隊列,並將它的左右子樹 BC加入隊列,此時隊列中有 ⇐[BC] ,打印出 A
我們將B出彈出隊列,它沒有子樹,我們不做任何操作,此時隊列中有 ⇐[C] ,打印出 ABC
我們將C出彈出隊列,並將它的左右子樹 DE加入隊列,此時隊列中有 ⇐[DE] ,打印出 ABC
我們將D出彈出隊列,它沒有子樹,我們不做任何操作,此時隊列中有 ⇐[E] ,打印出 ABCD
我們將E出彈出隊列,並將它的左右子樹 FG加入隊列,此時隊列中有 ⇐[FG] ,打印出 ABCDE
我們將F出彈出隊列,它沒有子樹,我們不做任何操作,此時隊列中有 ⇐[G] ,打印出 ABCDEF
我們將G出彈出隊列,它沒有子樹,我們不做任何操作,此時隊列中有 ⇐[null] ,打印出 ABCDEFG
結論:
根據軌跡我們不難發現,隊列是保證層序遍歷的基礎,因為它保證了先加入隊列的上層元素會必後加入隊列的下層元素優先出隊列。
2.這段代碼直接使用會出現問題,因為我們使用了C++標准模板庫中的queue。所以,我們需要加入頭文件
#include<queue>,並且要使用命名空間 using namespace std;。
3.我們對待數據結構最重要的是理解和使用,實現它只是幫助我們理解,我們無須重復造輪子,在以後的算法中,我們將盡可能的引用標准模板庫。