C高級 框架開發中紅黑樹結構,框架紅黑
引言 -- 紅黑樹歷史
紅黑樹是數據結構學習中一道卡. 底層庫容器中必不可少的算法. 歷經各種實戰運用,性能有保障. 同樣紅黑樹不好理解, 就算理解了, 代碼也不好寫.
就算寫了, 工程庫也難構建. 關於紅黑樹基礎講解推薦看下面博主的紅黑樹博文系列,感覺不錯.
紅黑樹(一)之 原理和算法詳細介紹
對於紅黑樹小背景簡介摘抄如下:
紅黑樹(英語:Red–black tree)是一種自平衡二叉查找樹,是在計算機科學中用到的一種數據結構,典型的用途是實現關聯數組。它是在1972年由魯道夫·貝爾發明的,他稱之為"對稱二叉B樹",它現代的名字是在Leo J. Guibas和Robert Sedgewick於1978年寫的一篇論文中獲得的。它是復雜的,但它的操作有著良好的最壞情況運行時間,並且在實踐中是高效的:它可以在O(log n)時間內做查找,插入和刪除,這裡的n是樹中元素的數目。
對於紅黑樹更加詳細的歷史參照下面資料.
紅黑樹 https://zh.wikipedia.org/wiki/%E7%BA%A2%E9%BB%91%E6%A0%91
本文重點介紹工程開發中, 紅黑樹工程基庫的封裝.直接用現成的最爽.
前言 -- 紅黑樹工程庫源碼
一言不合就上源碼!
rbtree.h
#ifndef _H_RBTREE
#define _H_RBTREE
struct rbnode {
unsigned long parent_color;
struct rbnode * right;
struct rbnode * left;
};
typedef void * (* new_f)(void *);
typedef int (* cmp_f)(const void *, const void *);
typedef void (* die_f)(void *);
typedef struct {
struct rbnode * root;
new_f new;
cmp_f cmp;
die_f die;
} * rbtree_t;
/*
* 每個想使用紅黑樹的結構, 需要在頭部插入下面宏.
* 例如 :
struct person {
_HEAD_RBTREE;
... // 自定義信息
};
*/
#define _HEAD_RBTREE struct rbnode __node
/*
* 創建一顆紅黑樹頭結點
* new : 注冊創建結點的函數
* cmp : 注冊比較的函數
* die : 注冊程序銷毀函數
* : 返回創建好的紅黑樹結點
*/
extern rbtree_t rb_new(new_f new, cmp_f cmp, die_f die);
/*
* 插入一個結點, 會插入 new(pack)
* tree : 紅黑樹頭結點
* pack : 待插入的結點當cmp(x, pack) 右結點
*/
extern void rb_insert(rbtree_t tree, void * pack);
/*
* 刪除能和pack匹配的結點
* tree : 紅黑樹結點
* pack : 當cmp(x, pack) 右結點
*/
extern void rb_remove(rbtree_t tree, void * pack);
/*
* 得到紅黑樹中匹配的結點
* tree : 匹配的結點信息
* pack : 當前待匹配結點, cmp(x, pack)當右結點處理
*/
extern void * rb_get(rbtree_t tree, void * pack);
/*
* 銷毀這顆二叉樹
* tree : 當前紅黑樹結點
*/
extern void rb_die(rbtree_t tree);
#endif /* _H_RBTREE */
rbtree.c

![]()
#include "rbtree.h"
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
/*
* 操作輔助宏, 得到紅黑樹中具體父結點, 顏色. 包括詳細設置信息
* r : 頭結點
* p : 父結點新值
* c : 當前顏色
*/
#define rb_parent(r) ((struct rbnode *)((r)->parent_color & ~3))
#define rb_color(r) ((r)->parent_color & 1)
#define rb_is_red(r) (!rb_color(r))
#define rb_is_black(r) rb_color(r)
#define rb_set_black(r) (r)->parent_color |= 1
#define rb_set_red(r) (r)->parent_color &= ~1
static inline void rb_set_parent(struct rbnode * r, struct rbnode * p) {
r->parent_color = (r->parent_color & 3) | (unsigned long)p;
}
static inline void rb_set_color(struct rbnode * r, int color) {
r->parent_color = (r->parent_color & ~1) | (1 & color);
}
static inline int _rb_cmp(const void * ln, const void * rn) {
return (const char *)ln - (const char *)rn;
}
/*
* 創建一顆紅黑樹頭結點
* new : 注冊創建結點的函數
* cmp : 注冊比較的函數
* die : 注冊程序銷毀函數
* : 返回創建好的紅黑樹結點
*/
rbtree_t
rb_new(new_f new, cmp_f cmp, die_f die) {
rbtree_t tree = malloc(sizeof(*tree));
if(NULL == tree) {
fprintf(stderr, "rb_new malloc is error!");
return NULL;
}
tree->root = NULL;
tree->new = new;
tree->cmp = cmp ? cmp : _rb_cmp;
tree->die = die;
return tree;
}
static inline struct rbnode * _rb_new(rbtree_t tree, void * pack) {
struct rbnode * node = tree->new ? tree->new(pack) : pack;
memset(node, 0, sizeof(struct rbnode));
return node;
}
/*
* 對紅黑樹的節點(x)進行左旋轉
*
* 左旋示意圖(對節點x進行左旋):
* px px
* / /
* x y
* / \ --(左旋)--> / \ #
* lx y x ry
* / \ / \
* ly ry lx ly
*
*/
static void _rbtree_left_rotate(rbtree_t tree, struct rbnode * x) {
// 設置x的右孩子為y
struct rbnode * y = x->right;
struct rbnode * xparent = rb_parent(x);
// 將 “y的左孩子” 設為 “x的右孩子”;
x->right = y->left;
// 如果y的左孩子非空,將 “x” 設為 “y的左孩子的父親”
if (y->left != NULL)
rb_set_parent(y->left, x);
// 將 “x的父親” 設為 “y的父親”
rb_set_parent(y, xparent);
if (xparent == NULL)
tree->root = y; // 如果 “x的父親” 是空節點,則將y設為根節點
else {
if (xparent->left == x)
xparent->left = y; // 如果 x是它父節點的左孩子,則將y設為“x的父節點的左孩子”
else
xparent->right = y; // 如果 x是它父節點的左孩子,則將y設為“x的父節點的左孩子”
}
// 將 “x” 設為 “y的左孩子”
y->left = x;
// 將 “x的父節點” 設為 “y”
rb_set_parent(x, y);
}
/*
* 對紅黑樹的節點(y)進行右旋轉
*
* 右旋示意圖(對節點y進行左旋):
* py py
* / /
* y x
* / \ --(右旋)--> / \ #
* x ry lx y
* / \ / \ #
* lx rx rx ry
*
*/
static void _rbtree_right_rotate(rbtree_t tree, struct rbnode * y) {
// 設置x是當前節點的左孩子。
struct rbnode * x = y->left;
struct rbnode * yparent = rb_parent(y);
// 將 “x的右孩子” 設為 “y的左孩子”;
y->left = x->right;
// 如果"x的右孩子"不為空的話,將 “y” 設為 “x的右孩子的父親”
if (x->right != NULL)
rb_set_parent(x->right, y);
// 將 “y的父親” 設為 “x的父親”
rb_set_parent(x, yparent);
if (yparent == NULL)
tree->root = x; // 如果 “y的父親” 是空節點,則將x設為根節點
else {
if (y == yparent->right)
yparent->right = x; // 如果 y是它父節點的右孩子,則將x設為“y的父節點的右孩子”
else
yparent->left = x; // (y是它父節點的左孩子) 將x設為“x的父節點的左孩子”
}
// 將 “y” 設為 “x的右孩子”
x->right = y;
// 將 “y的父節點” 設為 “x”
rb_set_parent(y, x);
}
/*
* 紅黑樹插入修正函數
*
* 在向紅黑樹中插入節點之後(失去平衡),再調用該函數;
* 目的是將它重新塑造成一顆紅黑樹。
*
* 參數說明:
* tree 紅黑樹的根
* node 插入的結點 // 對應《算法導論》中的z
*/
static void _rbtree_insert_fixup(rbtree_t tree, struct rbnode * node) {
struct rbnode * parent, * gparent, * uncle;
// 若“父節點存在,並且父節點的顏色是紅色”
while ((parent = rb_parent(node)) && rb_is_red(parent)) {
gparent = rb_parent(parent);
//若“父節點”是“祖父節點的左孩子”
if (parent == gparent->left) {
// Case 1條件:叔叔節點是紅色
uncle = gparent->right;
if (uncle && rb_is_red(uncle)) {
rb_set_black(uncle);
rb_set_black(parent);
rb_set_red(gparent);
node = gparent;
continue;
}
// Case 2條件:叔叔是黑色,且當前節點是右孩子
if (parent->right == node) {
_rbtree_left_rotate(tree, parent);
uncle = parent;
parent = node;
node = uncle;
}
// Case 3條件:叔叔是黑色,且當前節點是左孩子。
rb_set_black(parent);
rb_set_red(gparent);
_rbtree_right_rotate(tree, gparent);
}
else { //若“z的父節點”是“z的祖父節點的右孩子”
// Case 1條件:叔叔節點是紅色
uncle = gparent->left;
if (uncle && rb_is_red(uncle)) {
rb_set_black(uncle);
rb_set_black(parent);
rb_set_red(gparent);
node = gparent;
continue;
}
// Case 2條件:叔叔是黑色,且當前節點是左孩子
if (parent->left == node) {
_rbtree_right_rotate(tree, parent);
uncle = parent;
parent = node;
node = uncle;
}
// Case 3條件:叔叔是黑色,且當前節點是右孩子。
rb_set_black(parent);
rb_set_red(gparent);
_rbtree_left_rotate(tree, gparent);
}
}
// 將根節點設為黑色
rb_set_black(tree->root);
}
/*
* 插入一個結點, 會插入 new(pack)
* tree : 紅黑樹頭結點
* pack : 待插入的結點當cmp(x, pack) 右結點
*/
void
rb_insert(rbtree_t tree, void * pack) {
cmp_f cmp;
struct rbnode * node, * x, * y;
if((!tree) || (!pack) || !(node = _rb_new(tree, pack))) {
fprintf(stderr, "rb_insert param is empty! tree = %p, pack = %p.\n", tree, pack);
return;
}
cmp = tree->cmp;
// 開始走插入工作
y = NULL;
x = tree->root;
// 1. 將紅黑樹當作一顆二叉查找樹,將節點添加到二叉查找樹中。從小到大
while (x != NULL) {
y = x;
if (cmp(x, node) > 0)
x = x->left;
else
x = x->right;
}
rb_set_parent(node, y);
if (y != NULL) {
if (cmp(y, node) > 0)
y->left = node; // 情況2:若“node所包含的值” < “y所包含的值”,則將node設為“y的左孩子”
else
y->right = node; // 情況3:(“node所包含的值” >= “y所包含的值”)將node設為“y的右孩子”
}
else
tree->root = node; // 情況1:若y是空節點,則將node設為根
// 2. 設置節點的顏色為紅色
rb_set_red(node);
// 3. 將它重新修正為一顆二叉查找樹
_rbtree_insert_fixup(tree, node);
}
/*
* 紅黑樹刪除修正函數
*
* 在從紅黑樹中刪除插入節點之後(紅黑樹失去平衡),再調用該函數;
* 目的是將它重新塑造成一顆紅黑樹。
*
* 參數說明:
* tree 紅黑樹的根
* node 待修正的節點
*/
static void _rbtree_delete_fixup(rbtree_t tree, struct rbnode * node, struct rbnode * parent) {
struct rbnode * other;
while ((!node || rb_is_black(node)) && node != tree->root) {
if (parent->left == node) {
other = parent->right;
if (rb_is_red(other)) {
// Case 1: x的兄弟w是紅色的
rb_set_black(other);
rb_set_red(parent);
_rbtree_left_rotate(tree, parent);
other = parent->right;
}
if ((!other->left || rb_is_black(other->left)) &&
(!other->right || rb_is_black(other->right))) {
// Case 2: x的兄弟w是黑色,且w的倆個孩子也都是黑色的
rb_set_red(other);
node = parent;
parent = rb_parent(node);
}
else {
if (!other->right || rb_is_black(other->right)) {
// Case 3: x的兄弟w是黑色的,並且w的左孩子是紅色,右孩子為黑色。
rb_set_black(other->left);
rb_set_red(other);
_rbtree_right_rotate(tree, other);
other = parent->right;
}
// Case 4: x的兄弟w是黑色的;並且w的右孩子是紅色的,左孩子任意顏色。
rb_set_color(other, rb_color(parent));
rb_set_black(parent);
rb_set_black(other->right);
_rbtree_left_rotate(tree, parent);
node = tree->root;
break;
}
}
else {
other = parent->left;
if (rb_is_red(other)) {
// Case 1: x的兄弟w是紅色的
rb_set_black(other);
rb_set_red(parent);
_rbtree_right_rotate(tree, parent);
other = parent->left;
}
if ((!other->left || rb_is_black(other->left)) &&
(!other->right || rb_is_black(other->right))) {
// Case 2: x的兄弟w是黑色,且w的倆個孩子也都是黑色的
rb_set_red(other);
node = parent;
parent = rb_parent(node);
}
else {
if (!other->left || rb_is_black(other->left)) {
// Case 3: x的兄弟w是黑色的,並且w的左孩子是紅色,右孩子為黑色。
rb_set_black(other->right);
rb_set_red(other);
_rbtree_left_rotate(tree, other);
other = parent->left;
}
// Case 4: x的兄弟w是黑色的;並且w的右孩子是紅色的,左孩子任意顏色。
rb_set_color(other, rb_color(parent));
rb_set_black(parent);
rb_set_black(other->left);
_rbtree_right_rotate(tree, parent);
node = tree->root;
break;
}
}
}
if (node)
rb_set_black(node);
}
/*
* 刪除rb_get得到的結點
* root : 紅黑樹結點
* pack : 當cmp(x, pack) 右結點
*/
void
rb_remove(rbtree_t tree, void * pack) {
struct rbnode * child, * parent, * node = NULL;
int color;
if ((!tree) || !(node = (struct rbnode *)pack)) {
fprintf(stderr, "rb_remove check is error, tree = %p, node = %p.", tree, node);
return;
}
// 被刪除節點的"左右孩子都不為空"的情況。
if (NULL != node->left && node->right != NULL) {
// 被刪節點的後繼節點。(稱為"取代節點")
// 用它來取代"被刪節點"的位置,然後再將"被刪節點"去掉。
struct rbnode * replace = node;
// 獲取後繼節點
replace = replace->right;
while (replace->left != NULL)
replace = replace->left;
// "node節點"不是根節點(只有根節點不存在父節點)
if ((parent = rb_parent(node))) {
if (parent->left == node)
parent->left = replace;
else
parent->right = replace;
}
else
// "node節點"是根節點,更新根節點。
tree->root = replace;
// child是"取代節點"的右孩子,也是需要"調整的節點"。
// "取代節點"肯定不存在左孩子!因為它是一個後繼節點。
child = replace->right;
parent = rb_parent(replace);
// 保存"取代節點"的顏色
color = rb_color(replace);
// "被刪除節點"是"它的後繼節點的父節點"
if (parent == node)
parent = replace;
else {
// child不為空
if (child)
rb_set_parent(child, parent);
parent->left = child;
replace->right = node->right;
rb_set_parent(node->right, replace);
}
rb_set_parent(replace, rb_parent(node));
rb_set_color(replace, rb_color(node));
replace->left = node->left;
rb_set_parent(node->left, replace);
if (color) // 黑色結點重新調整關系
_rbtree_delete_fixup(tree, child, parent);
// 結點銷毀操作
if(tree->die)
tree->die(node);
return ;
}
if (node->left !=NULL)
child = node->left;
else
child = node->right;
parent = rb_parent(node);
// 保存"取代節點"的顏色
color = rb_color(node);
if (child)
rb_set_parent(child, parent);
// "node節點"不是根節點
if (parent) {
if (parent->left == node)
parent->left = child;
else
parent->right = child;
}
else
tree->root = child;
if (!color)
_rbtree_delete_fixup(tree, child, parent);
if(tree->die)
tree->die(node);
}
/*
* 得到紅黑樹中匹配的結點
* root : 匹配的結點信息
* pack : 當前待匹配結點, cmp(x, pack)當右結點處理
*/
void *
rb_get(rbtree_t tree, void * pack) {
cmp_f cmp;
struct rbnode * node;
if((!tree) || !pack) {
fprintf(stderr, "rb_get param is empty! tree = %p, pack = %p.\n", tree, pack);
return NULL;
}
cmp = tree->cmp;
node = tree->root;
while(node) {
int ct = cmp(node, pack);
if(ct == 0)
return node;
node = ct > 0 ? node->left : node->right;
}
return NULL;
}
// 後序遍歷刪除操作
static void _rb_die(struct rbnode * root, die_f die) {
if(NULL == root)
return;
_rb_die(root->left, die);
_rb_die(root->right, die);
die(root);
}
/*
* 銷毀這顆二叉樹
* root : 當前紅黑樹結點
*/
void
rb_die(rbtree_t tree) {
if(!tree || !tree->root || !tree->die)
return;
// 後續遞歸刪除
_rb_die(tree->root, tree->die);
// 銷毀樹本身內存
tree->root = NULL;
free(tree);
}
View Code
上面代碼主要基於linux內核中紅黑樹扒下來構建的工程庫. 有些細節我們簡單解釋一下結構. 例如
/*
* 每個想使用紅黑樹的結構, 需要在頭部插入下面宏.
* 例如 :
struct person {
_HEAD_RBTREE;
... // 自定義信息
};
*/
#define _HEAD_RBTREE struct rbnode __node
等同於'繼承'用法, 放在沒一個希望用在紅黑樹結構的頭部. 這些都是從linux內核結構中學到的技巧. libuv框架中也常用這種技巧.
也是C開發中通用潛規則! 還有一個技巧, 如下
struct rbnode {
unsigned long parent_color;
struct rbnode * right;
struct rbnode * left;
};
#define rb_parent(r) ((struct rbnode *)((r)->parent_color & ~3))
#define rb_color(r) ((r)->parent_color & 1)
也是在看內核源碼中學到的技巧, 將指針的後2位地址, 用於保存結點顏色. 為什麼可行呢,
因為 struct rbnode 結構體內存是以 sizeof (unsigned long) 大小對齊. 那麼該結構地址也是以 n*sizeof(unsigned long) 遞增.
後兩位都是0空出來的. 用於保存紅黑樹結點的顏色信息(RED | BLACK). 不得不佩服linux內核代碼的精巧.
後面還有一個自己補充的技巧
typedef void * (* new_f)(void *);
typedef int (* cmp_f)(const void *, const void *);
typedef void (* die_f)(void *);
typedef struct {
struct rbnode * root;
new_f new;
cmp_f cmp;
die_f die;
} * rbtree_t;
實現注冊, 創建, 比較, 銷毀行為函數, 方便使用. 采用匿名結構, 也是一個C中開發一個小技巧, 這個結構只能是堆上創建. 對外可見, 但是不可構建.
後面會基於這個紅黑樹基礎庫, 構建一個簡繁對照字典. 最後重申一下, 紅黑樹是軟件開發層最後的堡壘. 數據結構算法也就到這了.

正文 -- 簡單分析設計和測試
C的設計, 主要看結構. 同樣C的難點也是結構. 後面我們做一個簡單的簡繁轉換的字典, 通過C.
需要的資源見這個文件 http://files.cnblogs.com/files/life2refuel/C%E9%AB%98%E7%BA%A7%E5%B7%A5%E7%A8%8B%E4%B8%AD%E4%BD%BF%E7%94%A8%E7%BA%A2%E9%BB%91%E6%A0%91%E5%9F%BA%E5%BA%93.zip
簡繁變換的詞典,window上截圖如下
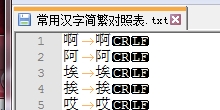
采用的是ascii編碼, 這裡一個漢字2字節表示. 上傳到linux上後, 采用utf-8編碼, 一個中文3個字節. 需要小心!
詞典主程序 main.c
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include "rbtree.h"
#define _STR_PATH "常用漢字簡繁對照表.txt"
#define _INT_DICT (4)
struct dict {
_HEAD_RBTREE;
char key[_INT_DICT];
char value[_INT_DICT];
};
// 需要注冊的內容
static void * _dict_new(void * arg) {
struct dict * node = malloc(sizeof(struct dict));
if (NULL == node) {
fprintf(stderr, "_dict_new malloc is error!\n");
return NULL;
}
*node = *(struct dict *)arg;
return node;
}
static inline int _dict_cmp(const void * ln , const void * rn) {
return strcmp(((const struct dict *)ln)->key, ((const struct dict *)rn)->key);
}
static inline void _dict_die(void * arg) {
free(arg);
}
// 創建內容
void dict_create(rbtree_t tree);
// 得到內容
const char * dict_get(rbtree_t tree, const char * key);
/*
* 這裡測試字典數據, 通過紅黑樹庫
*/
int main(int argc, char * argv[]) {
// 創建字典樹, 再讀取內容
rbtree_t tree = rb_new(_dict_new, _dict_cmp, _dict_die);
if (NULL == tree) {
fprintf(stderr, "main rb_new rb is error!\n");
return -1;
}
// 為tree填充字典數據
dict_create(tree);
// 我們輸出一下 '你好'
printf("你好嗎 -> %s%s%s\n",
dict_get(tree, "你"),
dict_get(tree, "好"),
dict_get(tree, "嗎")
);
// 字典書刪除
rb_die(tree);
getchar();
return 0;
}
// 創建內容
void
dict_create(rbtree_t tree) {
char c;
struct dict kv;
// 打開文件內容
FILE * txt = fopen(_STR_PATH, "rb");
if (NULL == txt) {
fprintf(stderr, "main fopen " _STR_PATH " rb is error!\n");
return;
}
while ((c = fgetc(txt))!=EOF) {
memset(&kv, 0, sizeof kv);
// 讀取這一行key, 並設值
kv.key[0] = c;
kv.key[1] = fgetc(txt);
// 去掉\\t
c = fgetc(txt);
if(c < 0) {
kv.key[2] = c;
fgetc(txt);
}
// 再設置value
kv.value[0] = fgetc(txt);
kv.value[1] = fgetc(txt);
c = fgetc(txt);
if (c != '\r') {// 這些SB的代碼, 都是解決不同系統版本的編碼沖突的
kv.value[2] = c;
fgetc(txt);
}
// 去掉\n
fgetc(txt);
// 插入數據
rb_insert(tree, &kv);
}
// 合法讀取內容部分
fclose(txt);
}
// 得到內容
const char *
dict_get(rbtree_t tree, const char * key) {
struct dict kv;
strncpy(kv.key, key, sizeof(kv.key) / sizeof(char));
struct dict * pkv = rb_get(tree, &kv);
return pkv ? pkv->value : NULL;
}
先看 window上測試結果
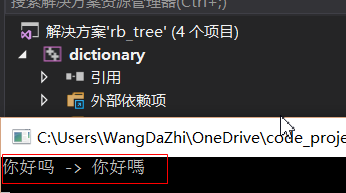
上面關於 dict_create 關於配置文件解析, 采用最原始的編碼字符數解析的.
linux上 測試過程如下


linux上測試結果很正常. 到這裡, 紅黑樹基庫demo演示完畢. 也許你覺得好復雜, 但是已經很簡單了. 因為C程序一個要求就是,
你需要懂得實現. 才能運用流暢. 一切都是鑽木取火, 自生自滅.
扯一點, C要是有那種萬能數據結構 array 或者 table 那生產率預估會提升10倍. 寫代碼就和玩似的.
今天完工等價於C基礎數據結構已經全線通工了. C的代碼寫的越多, 越發覺得喜歡就好!
後記 -- 一些客氣話
錯誤是難免的, 歡迎指正交流提高.
回家 http://music.163.com/#/song?id=157336







