樹與圖
3.5 二叉樹及其應用
PS:二叉樹是最經典的樹形結構,適合計算機處理,具有存儲方便和操作靈活等特點,而且任何樹都可以轉換成二叉樹。
實例101 二叉樹的遞歸創建 實例102 二叉樹的遍歷
問題:編程實現遞歸創建二叉樹,要求顯示樹的節點內容,深度及葉子節點數。
構造一棵二叉樹,分別采用先序遍歷、中序遍歷和後序遍歷遍歷該二叉樹。
邏輯:二叉樹是一棵由一個根節點(root)和兩棵互不相交的分別稱作根的左子樹和右子樹所組成的非空樹,左子樹和右子樹有同樣都是一棵二叉樹。
存儲二叉樹通常采用二叉鏈表法,即每個節點帶兩個指針和一個數據域(是不是突然覺得和鏈表很像呢),一個指針指向左子樹,另一個指針指向右子樹。
在遍歷二叉樹時若先左後右,則有三種遍歷方法,分別為先序遍歷、中序遍歷和後序遍歷,它們的遍歷定義如下:
先序遍歷:若二叉樹非空,則先訪問根結點,再按先序遍歷左子樹,最後按先序遍歷右子樹。
中序遍歷:若二叉樹非空,則先按中序遍歷左子樹,再訪問根結點,最後按中序遍歷右子樹。
後序遍歷:若二叉樹非空,則先按後序遍歷左子樹,再按後序遍歷右子樹,最後訪問根結點。
代碼:
1 #include<stdio.h>
2 #include<stdlib.h>
3
4 typedef struct node
5 //二叉鏈表的結構聲明
6 {
7 struct node *lchild;
8 char data;
9 struct node *rchild;
10 }bitnode,*bitree;
11 //結構體的類型。
12
13 bitree CreatTree()
14 //自定義函數CreatTree(),用於構造二叉樹。
15 {
16 char a;
17 bitree new;
18 scanf("%c",&a);
19 if(a=='#')
20 //二叉樹的輸入標識
21 return NULL;
22 else
23 {
24 new=(bitree)malloc(sizeof(bitnode));
25 //申請內存空間。
26 new->data=a;
27 new->lchild=CreatTree();
28 new->rchild=CreatTree();
29 }
30 return new;
31 }
32
33 void print(bitree bt)
34 //創建函數print(),用於輸出二叉樹的節點內容。PS:輸出方式為中序遍歷。
35 {
36 if(bt!=NULL)
37 {
38 print(bt->lchild);
39 printf("%c",bt->data);
40 print(bt->rchild);
41 }
42 }
43
44 int btreedepth(bitree bt)
45 //自定義函數btreedepth(),用於求解二叉樹的深度。
46 {
47 int ldepth,rdepth;
48 if(bt==NULL)
49 return 0;
50 else
51 {
52 ldepth=btreedepth(bt->lchild);
53 rdepth=btreedepth(bt->rchild);
54 return(ldepth>rdepth?ldepth+1:rdepth+1);
55 //返回語句中,采用了三目運算符。不知道的可以看該系列之前的篇章。
56 }
57 }
58
59 int ncount(bitree bt)
60 //自定義函數ncount(),用於求二叉樹中節點個數。
61 {
62 if(bt==NULL)
63 return 0;
64 else
65 return(ncount(bt->lchild)+ncount(bt->rchild)+1);
66 }
67
68 int lcount(bitree bt)
69 //自定義函數lcount(),用於求二叉樹中葉子節點個數。
70 {
71 if(bt==NULL)
72 return 0;
73 else if(bt->lchild==NULL && bt->rchild==NULL)
74 return 1;
75 else
76 return(lcount(bt->lchild)+lcount(bt->rchild));
77 }
78
79 void preorderTraverse(bitree bt)
80 //自定義函數preorderTraverse(),用於先序遍歷、輸出二叉樹。
81 {
82 if(bt!=NULL)
83 {
84 printf("%c",bt->data);
85 preorderTraverse(bt->lchild);
86 preorderTraverse(bt->rchild);
87 }
88 }
89
90 void InorderTraverse(bitree bt)
91 //自定義函數InorderTraverse(),用於中序遍歷、輸出二叉樹。
92 {
93 if(bt!=NULL)
94 {
95 InorderTraverse(bt->lchild);
96 printf("%c",bt->data);
97 InorderTraverse(bt->rchild);
98 }
99 }
100
101 void postorderTraverse(bitree bt)
102 //自定義函數postorderTraverse(),用於後序遍歷、輸出二叉樹。
103 {
104 if(bt!=NULL)
105 {
106 postorderTraverse(bt->lchild);
107 postorderTraverse(bt->rchild);
108 printf("%c",bt->data);
109 }
110 }
111
112 void main()
113 {
114 bitree root;
115 //初始化數據root。
116 root=CreatTree();
117 //調用函數創建二叉鏈表。
118 printf("contents of binary tree:\n");
119 print(root);
120 //調用函數輸出節點內容。
121 printf("\ndepth of binary tree:%d\n",btreedepth(root));
122 //調用函數輸出樹的深度。
123 printf("the number of the nodes:%d\n",ncount(root));
124 //調用函數輸出樹中節點個數。
125 printf("the number of the leaf nodes:%d\n",lcount(root));
126 //調用函數輸出樹中葉子節點個數。
127 printf("preorder traversal:\n");
128 preorderTraverse(root);
129 //調用函數先序遍歷輸出二叉樹。
130 printf("\n");
131 printf("inorder traversal:\n");
132 InorderTraverse(root);
133 //調用函數中序遍歷輸出二叉樹。
134 printf("\n");
135 printf("postorder traversal:\n");
136 postorderTraverse(root);
137 //調用函數後序遍歷輸出二叉樹。
138 printf("\n");
139 }
運行結果:
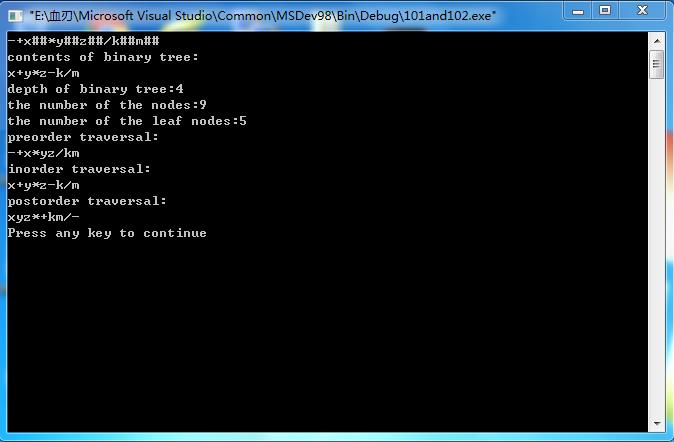
反思:整個程序代碼,並沒有多少新鮮東西。重要的是通過程序代碼,理解二叉樹創建、遍歷的概念。
二叉樹方面還有線索二叉樹、二叉排序樹等,但都不會打出代碼。因為代碼上並沒有新的內容,主要是對其概念的理解。
不過,其中的哈夫曼編碼還是得說說的。
實例105 哈夫曼編碼
問題:已知a,b,c,d,e,f各節點的權值分別為18、20、4、13、16、38,采用哈夫曼編碼法對各節點進行編碼。
邏輯:哈夫曼編碼算法:森林中共有n棵二叉樹,每棵二叉樹中僅有一個孤立的節點,他們既是根又是葉子,將當前森林中的兩棵根結點權值最小的二叉樹合並稱一棵新的二叉樹,每合並一次,森林中就減少一棵樹。森林中n棵樹要進行n-1次合並,才能使森林中的二叉樹的數目由n棵減少到一棵最終的哈夫曼樹。每次合並時都會產生一個新的節點,合並n-1次也就產生了n-1個新節點,所以最終求得的哈夫曼樹有2n-1個節點。
哈夫曼樹中沒有度為1的節點,實際上一棵具有n個葉子節點的哈夫曼樹共有2n-1個節點,可以存儲在一個大小為2n-1的一維數組中。在構建完哈夫曼樹後再求編碼需從葉子節點出發走一條從葉子到根的路徑。對每個節點我們既需要知道雙親的信息,又需要知道孩子節點的信息。
代碼:
1 #define MAXSIZE 50
2 #include<string.h>
3 #include<stdio.h>
4
5 typedef struct
6 //定義結構體huffnode,存儲節點信息。
7 {
8 char data;
9 //節點值
10 int weight;
11 //權值
12 int parent;
13 //父節點
14 int left;
15 //左節點
16 int right;
17 //右節點
18 int flag;
19 //標志位
20 }huffnode;
21 typedef struct
22 //定義結構體huffcode,存儲節點代碼。
23 {
24 char code[MAXSIZE];
25 int start;
26 }huffcode;
27 huffnode htree[2*MAXSIZE];
28 huffcode hcode[MAXSIZE];
29
30 int select(int i)
31 //自定義函數select(),用於尋找權值最小的節點。
32 {
33 int k=32767;
34 int j,q;
35 for(j=0;j<=i;j++)
36 if(htree[j].weight<k && htree[j].flag==-1)
37 {
38 k=htree[j].weight;
39 q=j;
40 }
41 htree[q].flag=1;
42 //將找到的節點標志位置1。
43 return q;
44 }
45
46 void creat_hufftree(int n)
47 //自定義函數creat_hufftree(),用於創建哈夫曼樹。
48 {
49 int i,l,r;
50 for(i=0;i<2*n-1;i++)
51 htree[i].parent=htree[i].left=htree[i].right=htree[i].flag=-1;
52 //全部賦值為-1.
53 for(i=n;i<2*n-1;i++)
54 {
55 l=select(i-1);
56 r=select(i-1);
57 //找出權值最小的左右節點。
58 htree[l].parent=i;
59 htree[r].parent=i;
60 htree[i].weight=htree[l].weight+htree[r].weight;
61 //左右節點權值相加等於新節點的權值。
62 htree[i].left=l;
63 htree[i].right=r;
64 }
65 }
66
67 creat_huffcode(int n)
68 //自定義函數creat_huffcode(),用於為各節點進行哈夫曼編碼。
69 {
70 int i,f,c;
71 huffcode d;
72 for(i=0;i<n;i++)
73 {
74 d.start=n+1;
75 c=i;
76 f=htree[i].parent;
77 while(f!=-1)
78 {
79 if(htree[f].left==c)
80 //判斷c是否是左子樹。
81 d.code[--d.start]='0';
82 //左邊編碼為0.
83 else
84 d.code[--d.start]='1';
85 //右邊編碼為1.
86 c=f;
87 f=htree[f].parent;
88 }
89 hcode[i]=d;
90 }
91 }
92
93 void display_huffcode(int n)
94 //創建函數display_huffcode(),用於輸出各節點的編碼。
95 {
96 int i,k;
97 printf("huffman is:\n");
98 for(i=0;i<n;i++)
99 {
100 printf("%c:",htree[i].data);
101 //輸出節點。
102 for(k=hcode[i].start;k<=n;k++)
103 printf("%c",hcode[i].code[k]);
104 //輸出各個節點對應的代碼。
105 printf("\n");
106 }
107 }
108
109 void main()
110 //定義主函數main(),作為程序的入口,用於輸入數據,調用函數。
111 {
112 int n=6;
113 htree[0].data='a';
114 htree[0].weight=18;
115 htree[1].data='b';
116 htree[1].weight=20;
117 htree[2].data='c';
118 htree[2].weight=4;
119 htree[3].data='d';
120 htree[3].weight=13;
121 htree[4].data='e';
122 htree[4].weight=16;
123 htree[5].data='f';
124 htree[5].weight=48;
125 creat_hufftree(n);
126 //調用函數創建哈夫曼樹。
127 creat_huffcode(n);
128 //調用函數構造哈夫曼編碼。
129 display_huffcode(n);
130 //顯示各節點哈夫曼編碼。
131 }
運行結果:
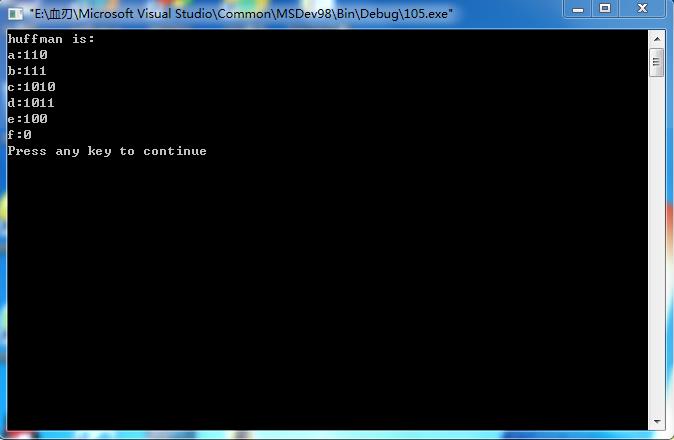
反思:整個過程,重在理解哈夫曼編碼的概念,以及編碼方式。如果有興趣,完全可以將主函數中的固定輸入,添加一個輸入函數,稍作修改,改為自主輸入。當然,如果有學過信息學的同學,更可以將其他編碼方式做成程序試試,有利於理解哦。
3.6 圖及圖的應用
PS:圖是一種比線性表和樹更為復雜的非線性結構。圖結構可以描述各種復雜的數據對象,特別是近年來迅速發展的人工智能、工程、計算科學、語言學、物理、化學等領域中。當然,這些都是套話。說白了,數據結構中復雜度極高的圖可以用來處理許多復雜數據,更為貼近現實的一些操作。
由於圖片問題,所以只闡述兩個例子的合例。
實例107 圖的深度優先搜索 實例108 圖的廣度優先搜索
問題:編程實現如圖所示的無向圖的深度優先搜索、廣度優先搜索。
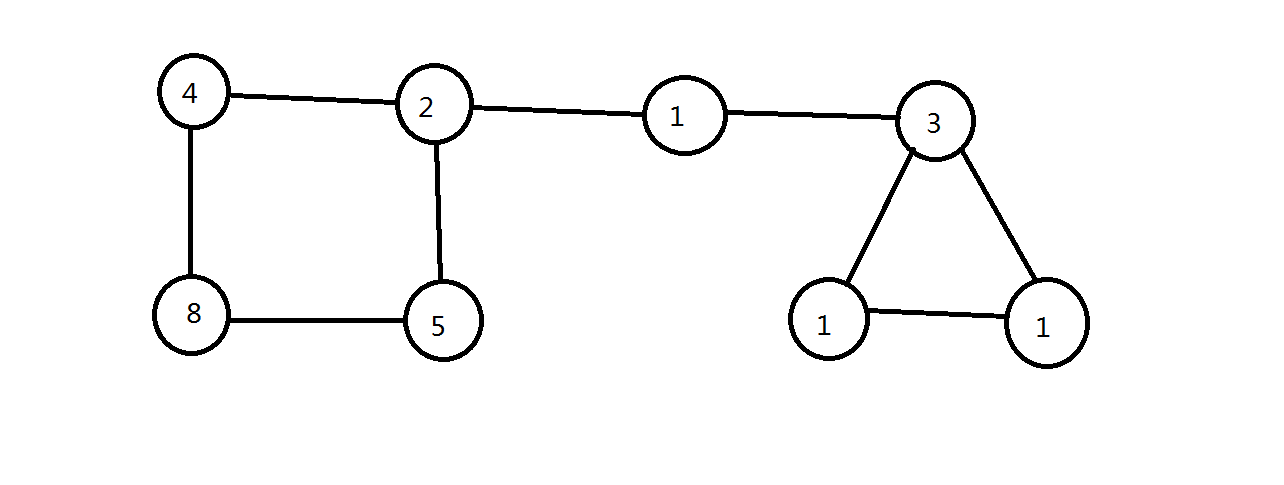
PS:圖片是自己畫的,將就一下吧。
邏輯:深度優先搜索即盡可能“深“的遍歷一個圖,在深度優先搜索中,對於最新已經發現的頂點,如果它的鄰接頂點未被訪問,則深度優先搜索該鄰接頂點。
廣度優先遍歷是連通圖的一種遍歷策略。其基本思想如下:
1、從圖中某個頂點V0出發,並訪問此頂點;
2、從V0出發,訪問V0的各個未曾訪問的鄰接點W1,W2,…,Wk;然後,依次從W1,W2,…,Wk出發訪問各自未被訪問的鄰接點;
3、重復步驟2,直到全部頂點都被訪問為止。
概念方面TODD911解釋得還是相當清晰的。
代碼:
1 #include<stdio.h>
2 #include<stdlib.h>
3
4 struct node
5 //圖的頂點結構
6 {
7 int vertex;
8 int flag;
9 struct node *nextnode;
10 };
11 typedef struct node *graph;
12 struct node vertex_node[10];
13
14 #define MAXQUEUE 100
15 int queue[MAXQUEUE];
16 int front=-1;
17 int rear=-1;
18 int visited[10];
19
20 void creat_graph(int *node,int n)
21 //自定義函數creat_graph(),用於構造鄰接表。
22 {
23 graph newnode,p;
24 //定義一個新節點及指針。
25 int start,end,i;
26 for(i=0;i<n;i++)
27 {
28 start=node[i*2];
29 //邊的起點。
30 end=node[i*2+1];
31 //邊的終點。
32 newnode=(graph)malloc(sizeof(struct node));
33 newnode->vertex=end;
34 //新節點的內容為邊終點處頂點的內容。
35 newnode->nextnode=NULL;
36 p=&(vertex_node[start]);
37 //設置指針位置。
38 while(p->nextnode!=NULL)
39 p=p->nextnode;
40 //尋找鏈尾。
41 p->nextnode=newnode;
42 //在鏈尾處插入新節點。
43 }
44 }
45
46 int enqueue(int value)
47 //自定義函數enqueue(),用於實現元素入隊。
48 {
49 if(rear>=MAXQUEUE)
50 return -1;
51 rear++;
52 //移動隊尾元素
53 queue[rear]=value;
54 }
55 int dequeue()
56 //自定義函數dequeue(),用於實現元素出隊。
57 {
58 if(front==rear)
59 return -1;
60 front++;
61 //移動隊首元素
62 return queue[front];
63 }
64
65 void dfs(int k)
66 //自定義函數dfs(),用於實現圖的深度優先遍歷。
67 {
68 graph p;
69 vertex_node[k].flag=1;
70 //將標志位置1,說明該節點已經被訪問過了。
71 printf("vertex[%d]",k);
72 p=vertex_node[k].nextnode;
73 //指針指向下一個節點。
74 while(p!=NULL)
75 {
76 if(vertex_node[p->vertex].flag==0)
77 //判斷該節點的標志位是否為0
78 dfs(p->vertex);
79 //繼續遍歷下一個節點
80 p=p->nextnode;
81 //如果已經遍歷過,p指向下一個節點
82 }
83 }
84
85 void bfs(int k)
86 {
87 graph p;
88 enqueue(k);
89 visited[k]=1;
90 printf("vertex[%d]",k);
91 while(front!=rear)
92 //判斷是否為空
93 {
94 k=dequeue();
95 p=vertex_node[k].nextnode;
96 while(p!=NULL)
97 {
98 if(visited[p->flag]==0)
99 //判斷是否訪問過。
100 {
101 enqueue(p->vertex);
102 visited[p->flag]=1;
103 //訪問過的元素變為1。
104 printf("vertexp[%d]",p->vertex);
105 }
106 p=p->nextnode;
107 //訪問下一個元素。
108 }
109 }
110 }
111
112 main()
113 {
114 graph p;
115 int node[100],i,sn,vn;
116 printf("please input the number of sides:\n");
117 scanf("%d",&sn);
118 //輸入無向圖的邊數。
119 printf("please input the number of vertexes:\n");
120 scanf("%d",&vn);
121 printf("please input the vertexes which connected by the sides:\n");
122 for(i=1;i<=4*sn;i++)
123 scanf("%d",&node[i]);
124 //輸入每個邊所連接的兩個頂點,起始及結束位置不同,每邊輸入兩次。
125 for(i=1;i<=vn;i++)
126 {
127 vertex_node[i].vertex=i;
128 //將每個頂點的信息存入數組中
129 vertex_node[i].flag=0;
130 vertex_node[i].nextnode=NULL;
131 }
132 creat_graph(node,2*sn);
133 //調用函數創建鄰接表
134 printf("the result is:\n");
135 for(i=1;i<=vn;i++)
136 {
137 printf("vertex%d:",vertex_node[i].vertex);
138 //將鄰接表頂點內容輸出
139 p=vertex_node[i].nextnode;
140 while(p!=NULL)
141 {
142 printf("->%3d",p->vertex);
143 //輸出鄰接頂點的內容
144 p=p->nextnode;
145 //指針指向下一個鄰接頂點
146 }
147 printf("\n");
148 }
149 printf("the result of depth-first search is:\n");
150 dfs(1);
151 //調用函數進行深度優先遍歷
152 printf("the result of breadth-first search is:\n");
153 bfs(1);
154 //調用函數進行廣度優先遍歷
155 printf("\n");
156 }
反思:其實,主要還是依靠鏈表那節的思路。所以說,這些數據結構,方法思路都是不變的。重要的還是理解其中的概念,即思想。至於圖當中的其他問題,如求最小生成樹等問題就不提了。
到這裡,數據結構章節已然完結了。
總結:數據結構在數據處理方面有著極其重要的地位。就算是考研,數據結構在計算機專業中,也占到了80',超過了專業分數一半。要知道計算機考研專業150'裡可是一共四門棵啊。所以,希望引起足夠重視。更為重要的是可以通過數據結構的程序,可以感受到編程中對數據,問題的處理方式,可以說就是編程思想的一點點體現了。
預告:接下來是算法一章。嗯。其實,看到有些書對算法的看法有兩種,一種認為算法很重要,是編程的靈魂。另一種認為算法並沒有那麼重要,更重要的編程的具體實現。我的看法是 算法體現編程思想,編程思想指引算法。
所以,下一章,我更加側重於思想,而不是具體代碼實現。
謝謝。
(表示我已經好幾次因為排版問題被踢出首頁區了。這次盡力了。真的就這排版水平了。。。。。。)