分治法與歸並排序,分治法歸並排序
本文部分內容參考了《算法導論》
分治策略
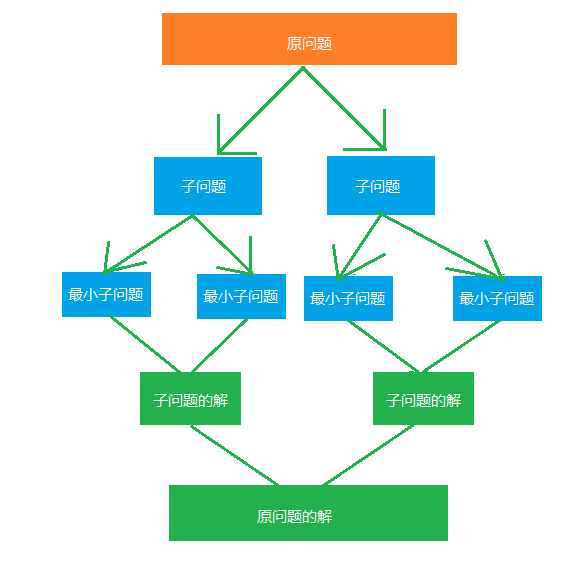
解決一個給定問題,算法需要一次或多次地遞歸調用自身來解決相關的子問題,這種算法通常采用分治策略。分治模式在每一層遞歸上都有三個步驟:
〉〉分解:將原問題分解成一系列子問題
〉〉解決:遞歸地求解各子問題。若子問題足夠小,則直接求解
〉〉合並:將子問題的結果合並成原問題的解。
歸並排序(合並排序)
歸並排序的關鍵在於歸並兩個相鄰的子序列,使其變成一個排序好的新序列。如果這個新序列就是原來需要進行排序的數組,那麼排序完成。所以,我們需要將原序列遞歸地分成若干子序列,直道最小的子序列只有一個元素,然後將子序列依次歸並,就可以得到排序好的原序列。我們要解決的第一個問題就是:假設有子序列A[p...q]和子序列[q + 1...r]是已經排序好的子序列,如何按順序將它們歸並到一個子序列中去呢?
歸並兩個子序列
我們可以用撲克牌做模擬。將兩堆數量相近的撲克牌按順序疊好,最小的牌放在最上面,牌面朝上。
〉〉第一步:拿出兩張中較小的一張,放在桌上。
〉〉第二步:分別比較所拿的牌和兩個堆上面的牌,重復第一步,跟在前一張牌的後面。直到一個堆拿完。
〉〉第三步:將剩余的堆從上往下一次放在桌上,跟在前一張牌的後面。
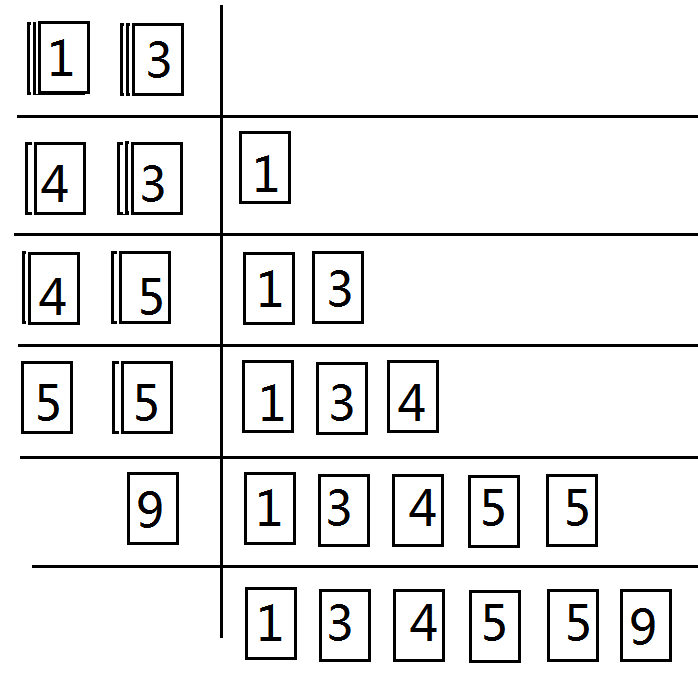
由此可見,按問題要求(加橙色的),我們可以設計如下代碼:
void merge(int ar[], int p, int q, int r, int temp[]){
//將ar[p...q]和ar[q+1...r]合並到temp[p...r],temp由外部分配內存
int i = p, j = q + 1, k = 0;
while(i <= q && j <= r){
if(ar[i] < ar[j])
temp[k++] = ar[i++];
else
temp[k++] = ar[j++];
}
while(i <= q) //如果ar[p..q]有剩
temp[k++] = ar[i++];
while(j <= r) //如果ar[q+1..r]有剩
temp[k++] = ar[j++];
for(k = 0; k <= (r - p); k++) //將合並後的子序列賦值給原序列ar[p...r]
ar[p + k] = temp[k];
}
對於歸並排序,我們要解決的第二個問題就是:原序列如何成為有序序列?
利用分治策略使原序列有序
我們可以通過將原序列二分為兩個子序列,再將兩個子序列二分為另外的四個子序列,直到不能再分解為止。然後分別合並相鄰的兩個子序列,直到不能合並為止。這裡引用網絡上的一張圖修改後來說明這個原理。
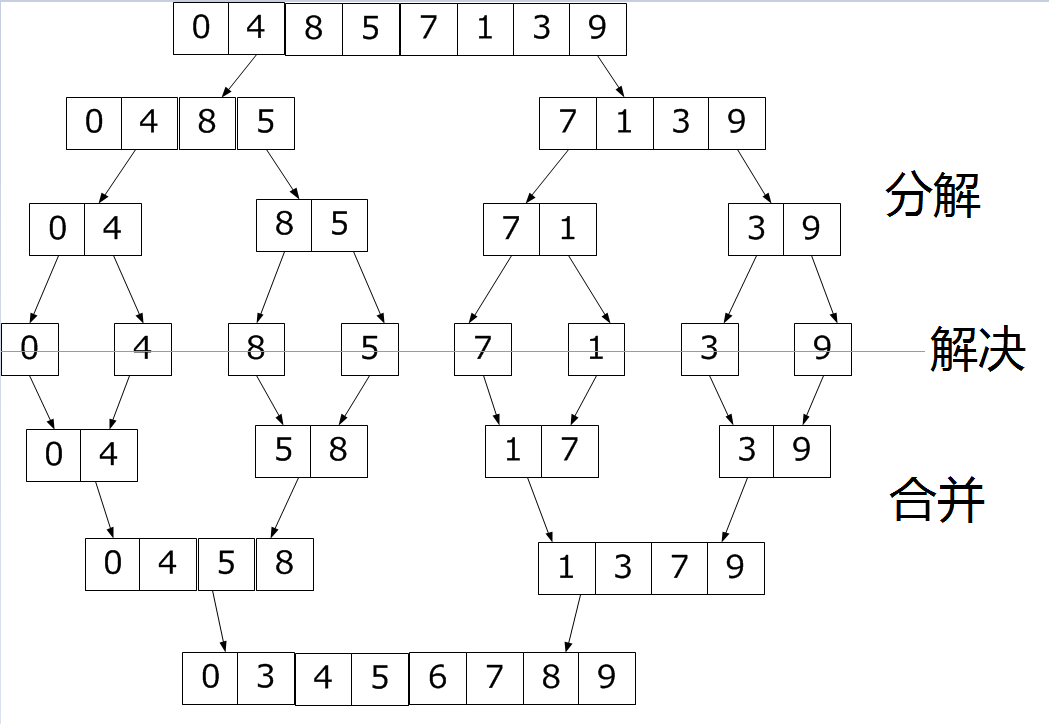
前面提到過,解決一個給定問題,算法需要一次或多次地遞歸調用自身來解決相關的子問題,這種算法通常采用分治策略。所以,我們可以利用分治策略通過通過遞歸調用一個函數來解決。我們可以這樣寫代碼:
void mergesort(int ar[], int head, int end, int temp[]){
if(head < end){ //條件:直到不能分割為止
int middle = (head + end) / 2; //找到二分原序列的點
mergesort(ar, head, middle, temp); //左子序列排序
mergesort(ar, middle + 1, end, temp); //右子序列排序
merge(ar, head, middle, end, temp); //合並這兩個子序列
}
}
分析上面的代碼,我們可以將上圖標上執行順序(建議在新窗口打開下圖),來驗證該算法的正確性。同時,你也可以通過類似“循環不變式”的方法證明:
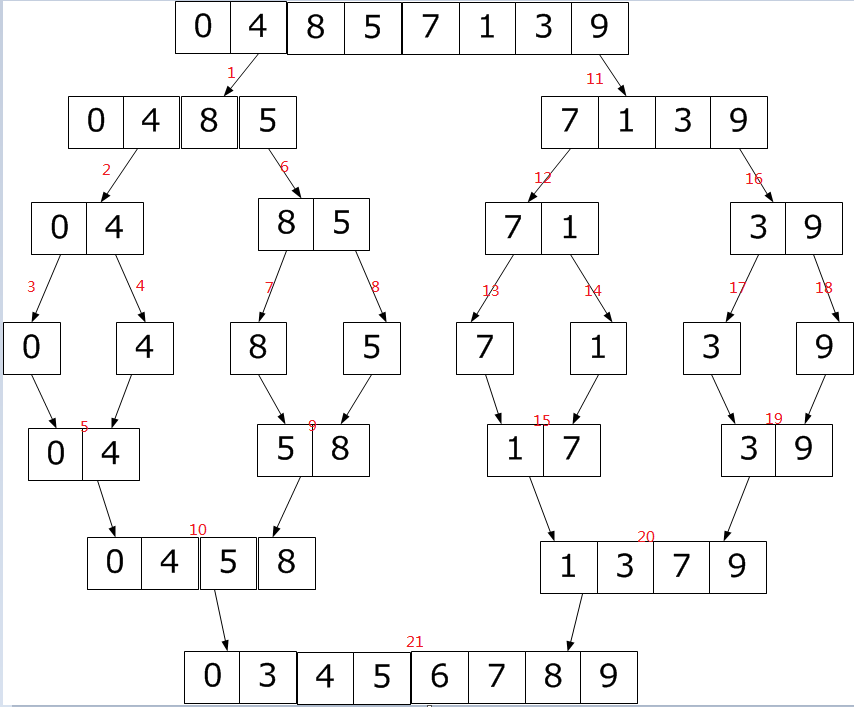
完整代碼
到這裡,歸並排序的所有問題都解決完了。我們給出完整的不帶注釋(分配內存後的空注釋是標志,提醒一定要及時釋放內存)的代碼。

![]()
1 #include <stdio.h>
2 #include <stdlib.h>
3 #include <conio.h>
4 #include <time.h>
5
6 void mergesort(int [], int, int, int []);
7 void merge(int [], int, int, int, int[]);
8
9 int main(int argc, char * argv[]){
10 int * ar, * temp;
11 int n = 10, i;
12
13 if( !(ar = (int *)malloc( (size_t)n * sizeof(int) ) ) )//
14 exit(EXIT_FAILURE);
15 if( !(temp = (int *)malloc( (size_t)n * sizeof(int) ) ) )//
16 exit(EXIT_FAILURE);
17
18 srand( (unsigned int)time(NULL) );
19 for(i = 0; i < n; i++){
20 ar[i] = rand() % 1000;
21 printf("%-4d",ar[i]);
22 }
23
24 mergesort(ar, 0, n - 1, temp);
25
26 printf("\n歸並排序後:\n");
27 for(i = 0; i < n; i++)
28 printf("%-4d",ar[i]);
29
30 free(temp);
31 free(ar);
32
33 _getch();
34 return 0;
35 }
36
37 void mergesort(int ar[], int head, int end, int temp[]){
38 if(head < end){
39 int middle = (head + end) / 2;
40 mergesort(ar, head, middle, temp);
41 mergesort(ar, middle + 1, end, temp);
42 merge(ar, head, middle, end, temp);
43 }
44 }
45
46 void merge(int ar[], int p, int q, int r, int temp[]){
47 int i = p, j = q + 1, k = 0;
48 while(i <= q && j <= r){
49 if(ar[i] < ar[j])
50 temp[k++] = ar[i++];
51 else
52 temp[k++] = ar[j++];
53 }
54 while(i <= q)
55 temp[k++] = ar[i++];
56 while(j <= r)
57 temp[k++] = ar[j++];
58
59 for(k = 0; k <= (r - p); k++)
60 ar[p + k] = temp[k];
61 }
MergeSort
下面這個是帶有入口函數的,只要在main()函數中把數組名和大小傳遞給mergesort()函數就行了。

![]()
1 #include <stdio.h>
2 #include <stdlib.h>
3 #include <conio.h>
4 #include <time.h>
5
6 void mergesort(float *, int);
7 void _mergesort(float *, int, int, float *);
8 void merge(float *, int, int, int, float *);
9
10 int main(int argc, char * argv[]){
11 float * ar;
12 int n = 10, i;
13
14 if( !(ar = (float *)malloc( (size_t)n * sizeof(float) ) ) )//
15 exit(EXIT_FAILURE);
16
17 srand( (unsigned int)time(NULL) );
18 for(i = 0; i < n; i++){
19 ar[i] = (float)((rand() % 499)) / (float)((rand() % 11 + 1));
20 printf("%-6.3g",ar[i]);
21 }
22
23 mergesort(ar, n);
24
25 printf("\n歸並排序後:\n");
26 for(i = 0; i < n; i++)
27 printf("%-6.3g",ar[i]);
28
29 free(ar);
30
31 _getch();
32 return 0;
33 }
34
35 void mergesort(float * ar, int size){
36 if(size > 0){
37 float * temp;
38 if(!(temp = (float *)malloc( (size_t)size * sizeof(float) ) ) ) //
39 exit(EXIT_FAILURE);
40 _mergesort(ar, 0, size - 1, temp);
41 free(temp);
42 }
43 }
44
45 void _mergesort(float * ar, int head, int end, float * temp){
46 if(head < end){
47 _mergesort(ar, head, (head + end) / 2, temp);
48 _mergesort(ar, (head + end) / 2 + 1, end, temp);
49 merge(ar, head, (head + end) / 2, end, temp);
50 }
51 }
52
53 void merge(float * ar, int p, int q, int r, float * temp){
54 int i = p, j = q + 1, k = 0;
55 while(i <= q && j <= r){
56 if( ar[i] < ar[j] )
57 temp[k++] = ar[i++];
58 else
59 temp[k++] = ar[j++];
60 }
61 while(i <= q)
62 temp[k++] = ar[i++];
63 while(j <= r)
64 temp[k++] = ar[j++];
65
66 for(k = 0; k <= (r - p); k++)
67 ar[p + k] = temp[k];
68 }
更好的MergeSort





