插入排序法較冒泡排序法和選擇排序法更貼近生活,應該來說理解起來更快。如果你現在能夠得到一副麻將,請把裡面的“一萬”到“六萬”拿出來,打亂順序,再重新排好,就像打麻將開始那樣。是否需要拿出某個麻將拿出來再插入其它麻將之間?這就是插入排序了。不過計算機沒有你那麼聰明,你只要小小幾步就可以將麻將排序好,而計算機還要一個一個地比較,但是,它超快的速度使你根本不知道它的笨拙!同樣,你也可以用撲克牌來試試,但是,這不是整個排序算法的重點,重點要看下面這幅圖,如果不理解,就看文章末尾附的《算法導論》中的圖(原數組(int []){5,6,3,2,1,4} ,每個數組都是排列好之後的,插入的元素就是沒有排列好之前i所指的元素):
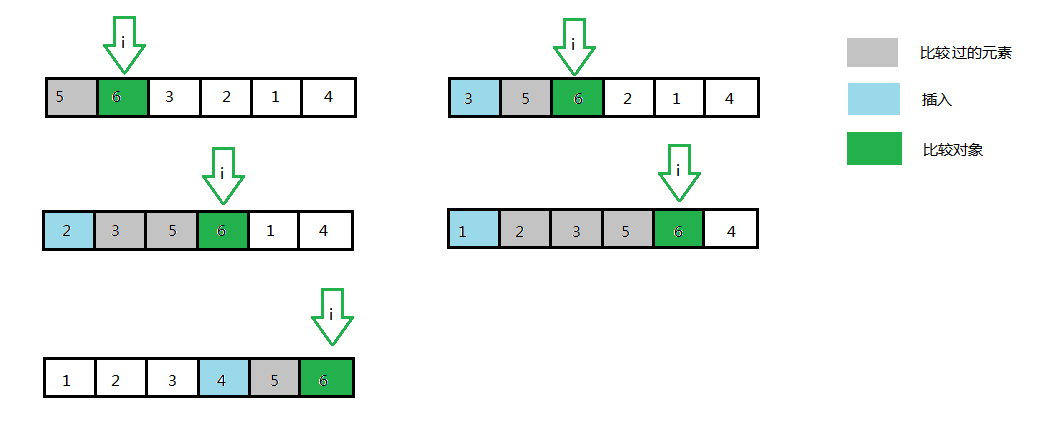
array[i]指向數組第2~最後一個元素,我們用array[j]表示第0~i之前的最後一個元素,通過依次比較array[i]與array[j],array[j - 1],...直到比較到比它小的元素。因為終止比較時,array[j]指向一個比要插入的元素小的元素,而array[j + 1]和array[j + 2]是內容相同的元素,因此,我們要把array[i]插入到array[j + 1]。
再來結合上圖看代碼(仔細分析,認真理解):
#include <stdio.h>
#include <stdlib.h>
#define SIZE 10
int main(int argc, char * argv[]){
int i, j, temp, array[SIZE] = {5,1,8,9,4,6,3,2,7,0};
for(i = 1; i < SIZE; i++){ //排序開始,把i初值定為數組第二個元素
temp = array[i]; //保存這個元素,然後方便比較和排序
for(j = i - 1; j >= 0 && array[j] > temp; j--)
//j最初表示i的前一個元素,通過與array[i]大小後,找到一個可插入的位置array[j + 1]
array[j + 1] = array[j];//大的元素向後移,關鍵!
array[j + 1] = temp; //插入!!!
}
for(i = 0; i < SIZE; i++)
printf("%-5d",array[i]);
getch();
return 0;
}
這裡需要注意的是,通過上圖觀察到array[0]~array[i]是已經排序好的數組,我們稱它為子數組,將array[i]後面的元素依次插入子數組直到沒有元素可以插入,這個子數組就是整個數組,排序完成。
有些地方出現的代碼和上面的代碼可能會不同,第二個循環我們用的是for而不是while。因為冒泡,選擇,排序這樣簡單的排序算法都可以用一個for循環嵌套另一個for循環表示,為了方便記憶,我使用了前者。這裡給出第二個循環用的是while的代碼:
#include <stdio.h>
#include <stdlib.h>
#define SIZE 10
int main(int argc, char * argv[]){
int i, j, temp, array[SIZE] = {5,1,8,9,4,6,3,2,7,0};
for(i = 1; i < SIZE; i++){ //道理是一樣的
j = i - 1;
temp = array[i];
while(j >= 0 && array[j] > temp){
array[j + 1] = array[j];
j--;
}
array[j + 1] = temp;
}
for(i = 0; i < SIZE; i++)
printf("%-5d",array[i]);
getch();
return 0;
}
如果不理解,請照著代碼把麻將或撲克牌排序幾遍!
運行結果:




