一、前言
在大家的認知過程中可能會認為計算機是不會出現計算錯誤的,但是實際上,依然存在程序運行後無法得到正確數值的情況。其中,最經典的就是小數運算。(做金融的一定要小心!!!)
二、引入
在我們的世界裡面,100個0.1相加就是10,這個是沒有疑問的。但是當我們用C語言如下的程序來計算的時候,結果並非是10(不同語言計算的結果可能不同,這裡主要說C)。
首先是一段計算代碼:
#include <stdio.h>
int main(void) {
float sum;
int i;
sum = 0;
for (i=0 ;i<100;i++) {
sum += 0.1;
}
printf("%f\n",sum);
}
運行結果如下:
10.000002
計算機通過編譯、鏈接、運行得到的結果是10.000002。程序沒有錯。現在讓我們來看一下具體原因吧。
三、計算機計算結果不正確的原因
簡單來說,就是無法表示正確的數值,導致計算出來的結果成了近似值。下面進一步剖析一下。
首先,我們來看一下在計算機世界裡面如何用二進制數表示小數:
例如把1011.0011這個小數點的二進制數轉成十進制數。(只需將各數位數值和位權相乘,然後將相乘的結果相加)
也就是:1*2^3+0*2^2+1*2^1+1*2^0+0*2^(-1)+0*2^(-2)+1*2^(-3)+1*2^(-4) = 11.1875。
了解了二進制表示的小數轉十進制的方法後,計算出錯的原因也就容易理解了。用小數點後4位用二進制表示時的數值范圍為:0.0000~0.1111。因此,對應的十進制結果如下:
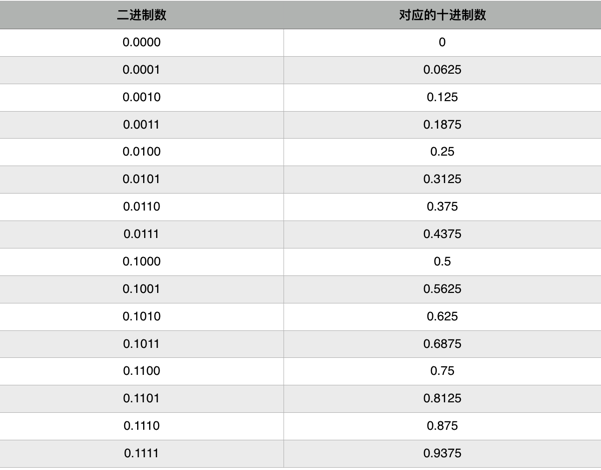
從上面的對照表可以看出,0的下一位就是0.625。因此0~0.0625之間的數值計算機無法用小數點後4位數的二進制數表示。因此可以看出0.1無法用4位二進制數表示。就算增加二進制的位數,也無法得到2^(-x) =0.1 這個結果。
實際上,十進制0.1轉成二進制後,就變成了0.0001100110011……(1100循環)這樣的循環小數。就像1/3是一個道理。因此100各0.1相加不等於10,而是等於近似值。
---------------------------------------------以上就能夠回答標題的原因了---------------------------------------------
四、What is 浮點數?
其實像剛才那樣的1011.0011這種表現形式完全是紙面上的二進制數表現形式,在計算機內部是無法使用的(計算機內部只是0101001……沒有"."這個概念)。實際上,編程語言提供了雙精度浮點數(double)和單精度浮點數(float)。雙精度浮點數類型用64位、單精度浮點數用32位來表示全體小數。
浮點數:就是用符號、尾數、基數和指數表示的小數。
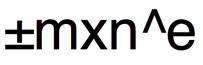
其中:±表示符號,m表示尾數,n表示基數,e表示指數。實際數據中不考慮基數。因此:

其中:
1、符號部分:1表示負、0表示正或者0。
2、尾數部分用的是:將小數點前面的值固定位1的正則表達式。
3、指數部分:用的是EXCESS系統表現。
先看看尾數部分。對於十進制的0.75。我們有如下的表示方法:
①、0.75 = 0.75*10^0
②、0.75 = 75*10^(-2)
③、0.75 = 0.075*10^1
十進制的表示正則為:小數點前面是0,小數點後面第一位不是0的規則表示。而對於二進制也是一樣的道理,使用的是:將小數點前面的值固定為1的正則。也就是將二進制數表示的小數左移或右移(邏輯移位)數次後,整數部分的第一位變成1,第二位之後變成0.而且第1位的1在實際數據中不保存。
例如1011.0011:
移位變成0001.0110011,確保小數點後23位:0001.01100110000000000000000,僅保留小數點後面完成正則:01100110000000000000000。
再看看指數部分。EXCESS系統表現:將指數部分表示范圍的中間值設置為0,使得負數不需要用符號來表示。例如當指數部分是8為單精度浮點時,最大值11111111=225的1/2即01111111=127表示0。雙精度類似。
因此對於單精度浮點數的表現,其表示范圍就是:00000000~11111111也就是-127~128。看下面例子:
#include <stdio.h>
#include <string.h>
int main(int argc, char *argv[]) {
float data;
unsigned long buff;
int i;
char n[34];
//將0.75以單精度浮點數形式存儲在data中
data = (float)0.75;
memcpy(&buff,&data,4);
for (i=33;i>=0;i--) {
if(i==1 || i==10) {
n[i] = '-';
}else {
if(buff%2==1) {
n[i] = '1';
}else {
n[i]='0';
}
buff/=2;
}
}
n[33] = '\0';
printf("%s\n",n);
}
運行結果:
0-01111110-10000000000000000000000
其中01111110是126,EXCESS表示為-1。
小數點前面的第一位是1。因此尾數就是:1.10000000000000000000000也就是1.5。
也就是+1.5*2^(-1) = 0.75。
五、如何避免小數計算出錯導致的問題
可以將小數替換成整數來計算。然後在縮小相應的倍數。
注:
1、如果有什麼Bug或者說的不對的地方,歡迎大家隨時提建議或者意見。