程式師世界 >> 編程語言 >> C語言 >> 關於C語言 >> C語言中遞歸什麼時候可以省略return引發的思考：通過內聯匯編解讀C語言函數return的本質

C語言中遞歸什麼時候可以省略return引發的思考：通過內聯匯編解讀C語言函數return的本質

編輯：關於C語言

C語言中遞歸什麼時候可以省略return引發的思考：通過內聯匯編解讀C語言函數return的本質

事情的經過是這樣的，博主在用C寫一個簡單的業務時使用遞歸，由於粗心而忘了寫return。結果發現返回的結果依然是正確的。經過半小時的反匯編調試，證明了我的猜想，現在在博客裡分享。也是對C語言編譯原理的一次加深理解。引子：首先我想以一道題目引例，比較能體現出問題。

例1：
#include 
/**
  函數功能:用遞歸實現位運算加法
 */
int Add_Recursion(int a,int b)
{
    int carry_num = 0, add_num = 0;
    if (b == 0)
    {
        return a;
    }
    else
    {
        add_num = a^b;
        carry_num = (a&b)<<1;
        Add_Recursion(add_num, carry_num);

    }
}
int main()
{

    int num = Add_Recursion(1, 1);

    printf("%d\n",num);
    getchar();
}

問題是，執行如上的程序，打印出來的數值是多少？大家可能會覺得這個非常的弱智，即使作為小公司的筆試題來說都登不上大雅之堂。

——————————–圖1 例題1的執行結果——————— 答案是2，毫無疑問，只是一個簡單的遞歸而已。
但是如果我把題目改一下

例2：
#include 
int changestack()
{
   return 3;
}
/**
  函數功能:用遞歸實現位運算加法
 */

int Add_Recursion(int a,int b)
{
    int carry_num = 0, add_num = 0;
    if (b == 0)
    {
        return a;
    }
    else
    {
        add_num = a^b;
        carry_num = (a&b)<<1;
        Add_Recursion(add_num, carry_num);
        changestack();

    }
}

int main()
{
    int num = Add_Recursion(1, 1);
    printf("%d\n",num);
    getchar();
}

大家看看上邊的程序，執行結果會是多少？
可能有很多朋友細心已經發現了貓膩。
可能也有部分朋友會有些困惑，這個程序只是在遞歸的實現函數後中加了一個無關緊要的函數調用，為什麼會影響函數返回的結果呢。
事實上printf打印出來的結果不正確。運行結果是3
圖2 例題2的執行結果

vcHLtO3O87XEt7W72Na1oaMNCjxwcmUgY2xhc3M9"brush:java;">

else
    {
        add_num = a^b;
        carry_num = (a&b)<<1;
        return Add_Recursion(add_num, carry_num);
         changestack();

    }

如果將上文的代碼改正如上，那不會出現任何問題。（當然不會出錯，此時有了return，return後邊的changestack根本就不會有任何機會執行）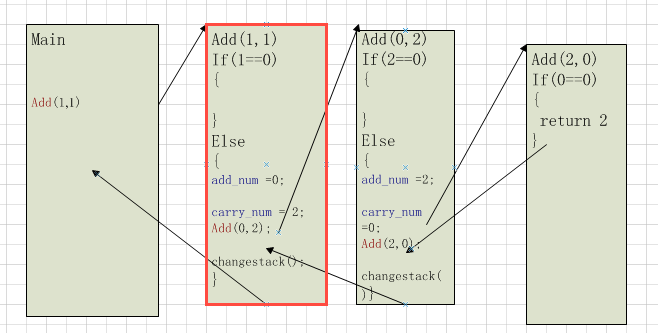
現在來一步一步來分析錯誤發生的本質。
這裡寫圖片描述

——————–圖三例二函數的遞歸分析—————————

我們分析上邊代碼的運行過程，首先在main函數中調用Add_Recursion(1,1),本意就是計算1+1的值，並且將函數返回值傳遞給printf打印出來。
在遞歸調用Add_Recursion函數(簡稱add)計算1+1時，前兩次遞歸調用由於不滿足遞歸出口條件（進位加數carry_num為0），會跳入else分支進行遞歸調用。直到第三次遞歸調用時由於carry_num為0，這時返回了累加結果。

問題是只有第三次的add遞歸調用進行了return，第一次和第二次在函數返回時，都沒有return，而是在返回子層次遞歸後調用changestack()函數後返回調用自己的函數層級。在第一層遞歸調用返回給main的時候,add_recursion並沒有return，而是在執行完changestack直接返回main函數，而此時main函數的printf在解析返回值時，實際上錯誤的解析了changestack的返回值。因此才出現1+1=3的錯誤綜上分析發生這一切的原因，就是：
函數執行結束返回時，會將返回值壓棧(理論上如此，實際上編譯器會優化，將返回值給eax寄存器過渡，VC就是使用的eax暫時保存)。VC編譯器解析函數返回值(整型)時，直接將eax的值讀出當做返回值。
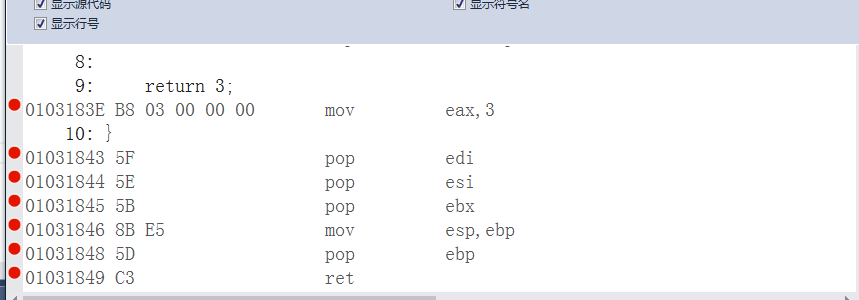
這裡寫圖片描述

———————-圖四反匯編分析VC編譯器對return的處理———- 根據反匯編分析可以看到，VC編譯器對changestack()中的return 3匯編的結果，也就是 mov eax,3。實際上就是把返回值賦予eax，由eax寄存器過渡給此函數的調用函數使用。

我們在下圖中可以看到main函數中將changestack()的返回值給num賦值的具體過程，也就是將eax的值返回給num的所在的內存地址。
這裡寫圖片描述
——————————圖五函數返回值的“彈棧”細則——————————-

這樣一切就有了解釋。

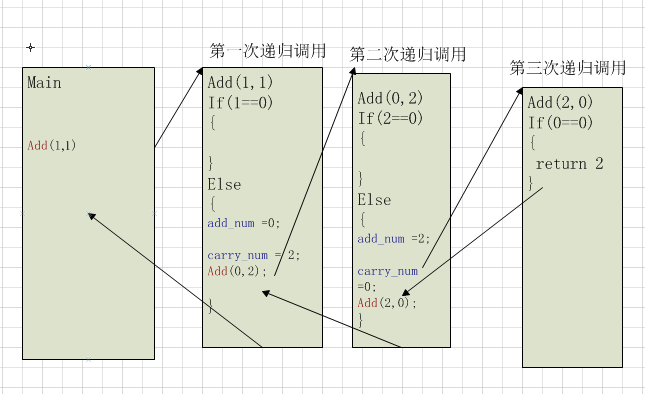
——————-圖六例題一為什麼會碰巧正確的遞歸分析—————

雖然第一題的結果雖然正確，printf在讀取Add_Recursion返回值時，讀取的不是第一次遞歸調用的結果，而是第三次遞歸調用return b的結果(第三次遞歸返回時，暫存在eax寄存器中)。而在之後的遞歸返回中，湊巧eax都沒有被改變。因此這樣使用遞歸（盡管沒有在需要return的地方return）是可以得到正確結果。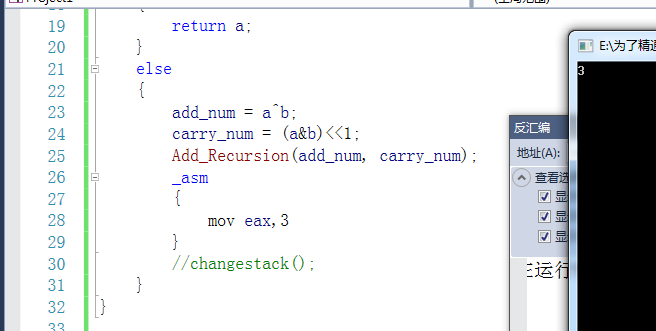
實際上我們可以用一條內聯匯編代碼驗證我們的猜想是否正確。我們在遞歸調用的後邊，使用內聯匯編加上一條匯編代碼改變eax的值。
這裡寫圖片描述