菲波那切數數列的幾種實現方法，數列

菲波那切數數列的幾種實現方法，數列

斐波那契數列：1，1，2，3，5，8，13，21……這個數列從第三項開始，每一項都等於前兩項之和。

如果設F(n)為該數列的第n項(n∈N+)。那麼菲波那切數列可以概括成如下形式：

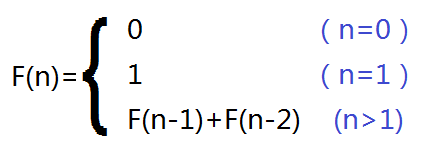
簡單的遞歸寫法：

long long FibonacciSeq(int n)
{
    if (n < 2)
    {
        return n;
    }
    return FibonacciSeq(n - 1) + FibonacciSeq(n - 2);
}

非遞歸循環方法：

這個方法只設置了三個變量，依次循環替換將結果放到數組的第三個變量中。這種方法雖然可讀寫差，但是當n的值很大時，它的效率要比遞歸的方法高很多。

long long FibonacciSeq(int n)   
{
    long long f[3] = { 0, 1,n };
 
    for (int i = 2; i <=n; i++)
    {
        f[2] = f[0] + f[1];
        f[0] = f[1];
        f[1] = f[2];
    }
    return f[2];
}

非遞歸的另一種方式就建立一個長度為n的數組，將數列中所有遍歷得到的結果都保存到了數組中。

long long FibonacciSeq(int n)
{
    long long fib[1000] = { 0, 1 };    
     
    for (int i = 2; i <= n; i++)
    {
        fib[i] = fib[i - 1] + fib[i - 2];
    }
    long long ret = fib[n];
    return ret;
}

上面的方法還不嚴謹，因為這裡數組的大小固定死了，如果n>1000就不好了，所以下面進行了優化：

long long FibonacciSeq( int n)
{
    if (n ==0)
    {
        return 0;
    }
    long long *fib=new long long[n+1];
    fib[0] = 0;
    fib[1] = 1;
    for (int i = 2;i <=n; i++)
    {
        fib[i] = fib[i - 1] + fib[i - 2];
    }
    long long ret = fib[n];
    delete[] fib;
    return ret;
}

或者用malloc開辟空間：

long long FibonacciSeq(int n)
{
    if (n == 0)
    {
        return 0;
    }
    long long *fib = (long long *)malloc(sizeof(long long)*(n + 1));
    fib[0] = 0;
    fib[1] = 1;
    for (int i = 2; i <= n; i++)
    {
        fib[i] = fib[i - 1] + fib[i - 2];
    }
    long long ret = fib[n];
    free(fib);
    return ret;
}

用new或者malloc為數組開辟空間的方法，一定要進行邊界條件檢查，否則程序可能會崩潰。

這裡給出 不進行邊界條件檢查時的代碼詳細分析 鏈接：new的越界訪問