組合數學之容斥原理

組合數學之容斥原理

在組合數學中，容斥是常常被用到的，我們總用容斥求解一些帶有條件的組合數。

• 容斥原理：具有性質A和性質B的元素個數等同於具有性質A的個數和具有性質B的個數的和再減去同時具有性質A和性質B的元素的個數。 
  數學公式表示為 |A∪B|=|A|+|B|-|A∩B|。 
  圖形表示為
   
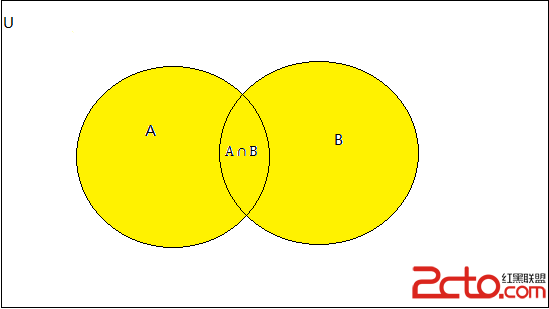
  其中黃色區域就是我們所求。 
  同樣以此類推對於三個性質來說其數學公式為|A∪B∪C|=|A|+|B|+|C|-|A∩B|-|A∩C|-|B∩C|+|A∩B∩C| 
  為什麼要加上最後那個呢？因為在減的過程中多減了一個。

• 對於容斥原理來說比較常用的方法為遞歸法和二進制枚舉法，二進制枚舉的方法最大的好處是枚舉出所有元素的子集。假設一個集合的元素有m個，則對於m長的二進制數來說就有m個1或0的位置，對於每一個1 
  -就對應一個元素，整個二進制枚舉完就是所有子集，從0到2^m就行。

• 遞歸法則是利用dfs的思想進行搜索，檢索每一種方案進行容斥。由於每一種題都有不同的搜索方法，沒用統一的模板，就不弄代碼了。

• 在這其中都是奇數個性質加偶數個性質減，而如果所求的性質是相反的性質，則用總數減去。
• 容斥原理開著簡單，實際非常復雜，每一道題都用不同的性質容斥，但最終的思想是不變的，多做一些題就會慢慢積累經驗最終由一個好的思想。