《算法（第四版）》排序-----快速排序

《算法（第四版）》排序-----快速排序

1.概念

快速排序，聽這個名字就能想到它排序速度快，它是一種原地排序（只需要一個很小的輔助棧，注意不是數組），且將長度為N的數組排序所需的時間和NlgN成正比

缺點是：非常脆弱，在實現時一定要注意幾個小細節（下面詳細講），才能避免錯誤。

2.基本思想：

隨機找出一個數（通常就拿數組第一個數據就行），把它插入一個位置，使得它左邊的數都比它小，它右邊的數據都比它大，這樣就將一個數組分成了兩個子數組，然後再按照同樣的方法把子數組再分成更小的子數組，直到不能分解為止。 它也是分治思想的一個經典實驗（歸並排序也是）

3.快速與歸並排序的區別：

（1）歸並排序將數組分成兩個子數組，然後分別排序，並將有序的子數組歸並以將整個數組排序；

快速排序將數組排序的方式是當兩個子數組都有序時整個數組也就自然有序了

（2）歸並排序的遞歸調用發生在處理整個數組之前

快速排序的遞歸調用發生在處理整個數組之後

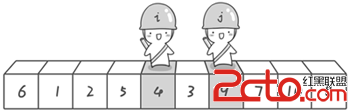
4.舉例說明 假設我們現在對“6 1 2 7 9 3 4 5 10 8”這個10個數進行排序。首先在這個序列中隨便找一個數作為基准數（不要被這個名詞嚇到了，就是一個用來參照的數，待會你就知道它用來做啥的了）。為了方便，就讓第一個數6作為基准數吧。接下來，需要將這個序列中所有比基准數大的數放在6的右邊，比基准數小的數放在6的左邊，類似下面這種排列。 3 1 2 5 4 69 7 10 8   在初始狀態下，數字6在序列的第1位。我們的目標是將6挪到序列中間的某個位置，假設這個位置是k。現在就需要尋找這個k，並且以第k位為分界點，左邊的數都小於等於6，右邊的數都大於等於6。想一想，你有辦法可以做到這點嗎？   給你一個提示吧。請回憶一下冒泡排序，是如何通過“交換”，一步步讓每個數歸位的。此時你也可以通過“交換”的方法來達到目的。具體是如何一步步交換呢？怎樣交換才既方便又節省時間呢？先別急著往下看，拿出筆來，在紙上畫畫看。我高中時第一次學習冒泡排序算法的時候，就覺得冒泡排序很浪費時間，每次都只能對相鄰的兩個數進行比較，這顯然太不合理了。於是我就想了一個辦法，後來才知道原來這就是“快速排序”，請允許我小小的自戀一下(^o^)。  

方法其實很簡單：分別從初始序列“6 1 2 7 9 3 4 5 10 8”兩端開始“探測”。先從右往左找一個小於6的數，再從左往右找一個大於6的數，然後交換他們。這裡可以用兩個變量i和j，分別指向序列最左邊和最右邊。我們為這兩個變量起個好聽的名字“哨兵i”和“哨兵j”。剛開始的時候讓哨兵i指向序列的最左邊（即i=1），指向數字6。讓哨兵j指向序列的最右邊（即j=10），指向數字8。

 

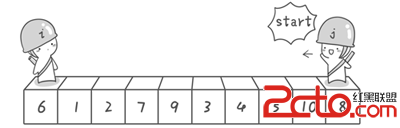
首先哨兵j開始出動。因為此處設置的基准數是最左邊的數，所以需要讓哨兵j先出動，這一點非常重要（請自己想一想為什麼）。哨兵j一步一步地向左挪動（即j--），直到找到一個小於6的數停下來。接下來哨兵i再一步一步向右挪動（即i++），直到找到一個數大於6的數停下來。最後哨兵j停在了數字5面前，哨兵i停在了數字7面前。

 

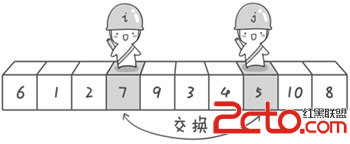
現在交換哨兵i和哨兵j所指向的元素的值。交換之後的序列如下。

6 1 2 59 3 4 710 8

 

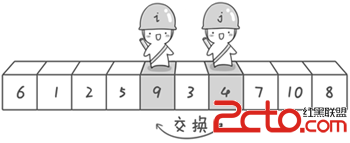
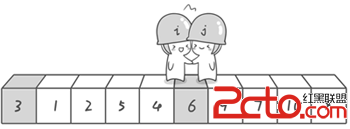
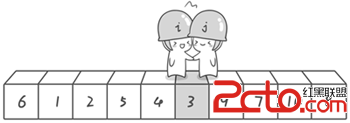
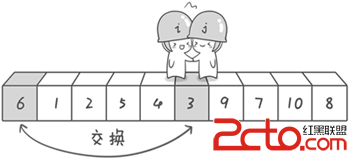
到此，第一次交換結束。接下來開始哨兵j繼續向左挪動（再友情提醒，每次必須是哨兵j先出發）。他發現了4（比基准數6要小，滿足要求）之後停了下來。哨兵i也繼續向右挪動的，他發現了9（比基准數6要大，滿足要求）之後停了下來。此時再次進行交換，交換之後的序列如下。 6 1 2 5 43 97 10 8   第二次交換結束，“探測”繼續。哨兵j繼續向左挪動，他發現了3（比基准數6要小，滿足要求）之後又停了下來。哨兵i繼續向右移動，糟啦！此時哨兵i和哨兵j相遇了，哨兵i和哨兵j都走到3面前。說明此時“探測”結束。我們將基准數6和3進行交換。交換之後的序列如下。 31 2 5 4 69 7 10 8 、 到此第一輪“探測”真正結束。此時以基准數6為分界點，6左邊的數都小於等於6，6右邊的數都大於等於6。回顧一下剛才的過程，其實哨兵j的使命就是要找小於基准數的數，而哨兵i的使命就是要找大於基准數的數，直到i和j碰頭為止。   OK，解釋完畢。現在基准數6已經歸位，它正好處在序列的第6位。此時我們已經將原來的序列，以6為分界點拆分成了兩個序列，左邊的序列是“3 1 2 5 4”，右邊的序列是“9 7 10 8”。接下來還需要分別處理這兩個序列。因為6左邊和右邊的序列目前都還是很混亂的。不過不要緊，我們已經掌握了方法，接下來只要模擬剛才的方法分別處理6左邊和右邊的序列即可。現在先來處理6左邊的序列現吧。   左邊的序列是“3 1 2 5 4”。請將這個序列以3為基准數進行調整，使得3左邊的數都小於等於3，3右邊的數都大於等於3。好了開始動筆吧。   如果你模擬的沒有錯，調整完畢之後的序列的順序應該是。 2 1 35 4   OK，現在3已經歸位。接下來需要處理3左邊的序列“2 1”和右邊的序列“5 4”。對序列“2 1”以2為基准數進行調整，處理完畢之後的序列為“1 2”，到此2已經歸位。序列“1”只有一個數，也不需要進行任何處理。至此我們對序列“2 1”已全部處理完畢，得到序列是“1 2”。序列“5 4”的處理也仿照此方法，最後得到的序列如下。 1 2 3 4 5 6 9 7 10 8   對於序列“9 7 10 8”也模擬剛才的過程，直到不可拆分出新的子序列為止。最終將會得到這樣的序列，如下。 1 2 3 4 5 6 7 8 9 10   到此，排序完全結束。細心的同學可能已經發現，快速排序的每一輪處理其實就是將這一輪的基准數歸位，直到所有的數都歸位為止，排序就結束了。下面上個霸氣的圖來描述下整個算法的處理過程。
  快速排序之所比較快，因為相比冒泡排序，每次交換是跳躍式的。每次排序的時候設置一個基准點，將小於等於基准點的數全部放到基准點的左邊，將大於等於基准點的數全部放到基准點的右邊。這樣在每次交換的時候就不會像冒泡排序一樣每次只能在相鄰的數之間進行交換，交換的距離就大的多了。因此總的比較和交換次數就少了，速度自然就提高了。當然在最壞的情況下，仍可能是相鄰的兩個數進行了交換。因此快速排序的最差時間復雜度和冒泡排序是一樣的都是O(N²)，它的平均時間復雜度為O(NlogN)。其實快速排序是基於一種叫做“二分”的思想。 

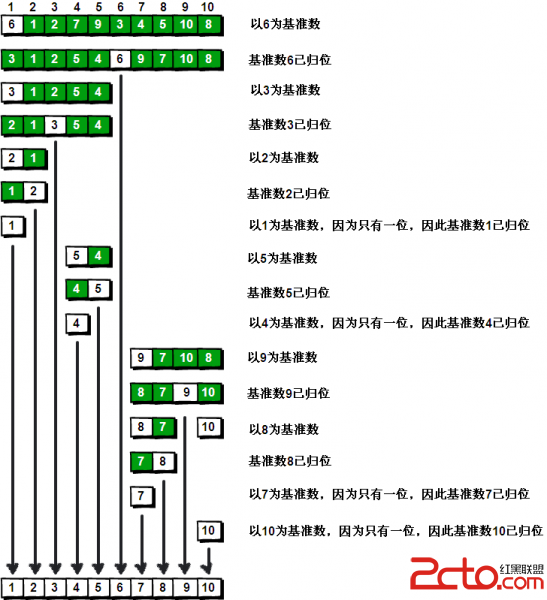
5.具體實現如下：

public class QuickSort{
    public static void quickSort(Comparable[] a){
        //StdRandom.shuffle(a);//將數組a順序打亂，消除對輸入的依賴，這是《算法第四版》作者寫好的靜態函數，
        quickSort(a, 0, a.length-1);
    }
    public static void quickSort(Comparable[] a, int lo, int hi){
        if(hi <= lo)    //跳出遞歸的條件，相當於不能再分解了
            return;
        int j = partition(a, lo, hi);    //切分（將a[lo]插入到數組中合適的位置：左邊比他小，右邊比它大，這樣就將數組切分成兩部分）
        quickSort(a, lo, j-1);           //將左半部分a[lo...j-1]排序
        quickSort(a, j+1, hi);           //將右半部分a[j+1...hi]排序
    }
    private static int partition(Comparable[] a, int lo, int hi){
    //將數組切分為a[lo...i-1]、a[i] 和a[i+1...hi];
        int i = lo, j = hi + 1;   //左右掃描的指針,j=hi+1,很大的程度上是為了下面寫--j，
        Comparable v = a[lo];     //把要用來切分的元素保留
        while(true){              // 掃描左右檢查掃描是否結束並交換元素
            while(less(a[++i], v))//兩種條件會跳出while循環，直到在左側找到比v大的，或i指針已經走到頭了（i==hi）,++i的原因：v是從lo開始的，滿足less（）
                if(i == hi)   break;//不過這兩個判斷越界的測試條件是多余的，可以去掉，因為本身i,j就是從兩端走過去的，不等走到頭就
            while(less(v,a[--j]));
                if(j == lo)   break;
            if(i >= j)    break;  //i和j碰上了，那就跳出整個循環，
            exch(a,i,j);          //如果上兩個while都跳出，說明i，j停在了a[i]>v ，a[j]
6.注意：
（1）處理切分元素值有重復的情況，所以左側掃描最好是遇到 >= 切分元素值的元素時停下，右側掃描遇到 <= 切分元素值的元素時停下，這樣能比秒算法運行時間平方級別
（2）終止遞歸：一定保證終止遞歸的條件，否則就遞歸陷入死循環了
7.算法改進
7.1 切換到插入排序
和大多數遞歸排序算法一樣，改進快速排序性能的一個簡單辦法是基於以下兩點：
（1）對於小數組，快速排序比插入排序慢
（2）因為遞歸，快速排序的sort（）方法在小數組中也會調用自己
因此，在排序小數組應該切換到插入排序，簡單的改動算法中的一句就可：將sort（）中的語句
                   if(hi <= lo)  return;
改成：            if(hi <= lo + M){Insertion.sort(a, lo, hi);  return; }
這樣就可以在小數組時轉換成插入排序
轉換參數M的最佳值是和系統相關的，但是5~15 之間的惹你值在大多數情況下都能令人滿意
 
7.2 三取樣切分
改進快速排序性能的第二個辦法就是使用子數組的一小部分元素的中位數來切分數組，這樣做得到的切分效果更好，但是代價是要計算中位數。人們發現將取樣大小設為3並用大小居中的元素氣氛效果最好，我們還可以將取樣元素放在數組末尾作為“哨兵”來去掉partition（）中的數組邊界測試。
 


7.3 熵最有的排序
實際應用中經常會出現含有大量重復元素的數組，例如我們可能需要將大量人員資料按照生日排序，或是按照性別區分開來，在這種情況下，我們事先的快速排序還有很大的改進空間。
簡單的想法是將數組分為三部分，分別對應小於，等於和大於切分元素的數組元素，這也是荷蘭國旗引發的易到景點編程練習，因為這就好像用三種可能的主鍵值將數組排序一樣，這三種主鍵值對應這荷蘭國旗上的三種顏色。
三向切分的快速排序算法思想如下：
它從左到右遍歷數組一次，維護一個指針lt使a[lo...lt-1]中的元素都小於v,一個指針gt使得a[gt+1...hi]中的元素都大於v，一個指針i使得a[lt...i-1]中的元素都等於v,a[i...gt]中的元素都還未確定。
（1）a[i] < v   將a[lt]和a[i]交換，將lt和i加一
（2）a[i] > v   將a[gt]和a[i]交換，將gt減一
（3）a[i] = v   將i加一
lt++的原因：lt相當於v的當前位置，a[lt] =v，所以只有當a[lt] >a[i]時才會交換，交換後v之前就多了一個值，所以lt++
i++的原因：有兩種情況i++,第一種a[i] < v，這樣必然會將a[i] 這個值換到v之前，然而一直在動的那個指針就是i，所以i要向前走，比較下一個a[i] 與v的大小，如果相等自動加一
gt--的原因：交換a[gt]和a[i]的原因是，a[i]>v了，那麼肯定a[i]的值滿足了在v後面,索性把這個大於v的就放最後面，肯定滿足v後面的都比它大，所以把a[gt]拿過來，此時還不能             保 證a[gt]的大小，所以放到i這個位置上，在下一輪比較a[i].compareTo(v)，就能確定拿過來的a[gt]到底比v大還是小了，但是已經確定由a[i]和a[gt]交換後的a[gt]肯         
    定比 v 大，所以沒有必要下一輪交換時再交換到前面去，所以gt減一
具體實現代碼如下
public  class Quick3Way{
    private static void sort(Comparable[] a, int lo, int hi){
        if(hi <= lo)    return ;
        int lt = lo, i = lo+1, gt = hi;
        Comparable v = a[lo];
        while (i <= gt){
            int cmp = a[i].compareTo(v);
            if  (cmp < 0){   exch(a, lt++, i++);
            }else if(cmp > 0){  exch(a, i, gt--);
            }else{
                i++;
            }
        }//  現在a[lo...lt-1] < v = a[lt...gt] < a[gt+1...hi]成立
        sort(a, lo, lt-1);
        sort(a, gt+1, hi);
    }
}
 
圖示交換過程：

 
所以可以看出，當數組中的元素存在大量的重復數據的時候，三向切分的快速排序效果更好