淺談DP算法(一)
——如何用一維數組解決01背包問題
DP算法(Dynamic Programming,俗稱動態規劃)是最經典算法之一.本筆記以耳熟能詳的數塔問題為引子,深入討論01背包的解決方法.
首先,如下圖所示,要求從頂層走到底層,若每一步只能走到相鄰的結點,則經過的結點的數字之和最大是多少?
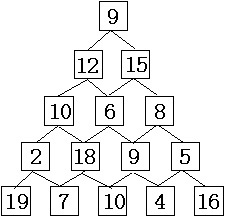
這個問題,對於任意一個結點,直接選擇數字大的子結點顯然是不行的.以9為例,如果選擇15,當前和24>21,但是15的兩個子結點太小,24+6+18<21+10+18.由此可見,這樣求出每階段的部分最優解並不是全局最優解.另外,如果用蠻力算法,每條路徑都遍歷一次,那麼層數為n時,路徑總數呈指數級增長:
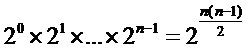
顯然這種方法的計算量太大,也不可取.那麼此時用DP算法是行之有效的.具體思想為:從倒數第二層開始,一層一層向上遍歷.倒數第二層第一個結點是2,如果路徑經過2,那麼肯定會選擇數值較大左子結點19. 便用19+2=21代替原先的2. 同理18改為18+10=28,9改為19,5改為21. 這樣倒數第二層就變成21 28 19 21四個結點,再將最後一層捨棄.這樣一層層向上,直到第一層,選擇第二層較大的那個結點加到9上面去,就得出了全局最優解.
代碼實現:如果數字塔為n層,開辟一個n*n的二維數組即可,非常簡單,此處省略.
對動態規劃的思想有一個基本了解後,現總結出動態規劃基本概念.不過在此之前,首先解釋一下什麼是多階段決策問題,什麼是狀態.
多階段決策問題:一個問題可以分為若干個階段,每個階段都要做出決策;
狀態:每個階段開始面臨的自然狀況或客觀條件.在上例中每個階段的狀態就是到達當前結點的兩個子結點的選擇.
動態規劃是一個多階段決策問題中,各個階段采取的決策,依賴於當前狀態,又引起狀態的轉移,一個決策序列就是在變化的狀態中產生出來的,故有“動態”的含義,稱這種解決多階段決策最優化問題的方法為動態規劃方法.
適用DP算法的問題一般具備以下特點:
(1)最優化原理(最優子結構性質)
一個最優化策略的子策略也是最優的.舉個例子就清楚了,如數字塔問題中,第二層到底層數值和最大的路徑一定是從頂層到底層數值和最大的路徑的子集;
(2)無後向性(無後效性)
通俗講,某階段狀態一旦確定,就不受這個狀態之後的決策的影響;
(3)子問題重疊
即子問題之間不獨立.與前兩個不同的是,這個特點不是必要的,如果不滿足相比之下DP算法不具備優勢.如果獨立,分治算法策略將更簡單方便.
下面來看經典的01背包問題:
把N個物品放入容量為V的背包裡,第i個物品所需要的空間為need[i],同時它的價值為value[i],該如何放才能達到背包裡的物品價值最大?
分析:因為對於任何一個物品,都只有放或不放的選擇,因而稱之為01背包.用best(N,V)*表示N個物品放入容量為V的背包裡的最大價值.則對於第N個物品,除非need[N]>V,都有放或不放兩個選擇:
(1)如果將第N個物品放入背包中
best(N,V)=best(N-1,V-need[N])+value[N]; //即等於第N個物品的價值加上將N-1個物品放入容量為V-need[N]的背包裡的最大價值;
(2)如果不放
best(N,V)=best(N-1,V-need[N])+value[N]; //即等於第N個物品的價值加上將N-1個物品放入容量為V-need[N]的背包裡的最大價值;
這樣我們重復上述步驟,直至N和V減小到0,可以得到對於其中任何一個物品i (1<=i<=N),當前狀態背包剩余容量為j (0<=j<=V),都有
if(j<need[i])
best(i,j)=best(i-1,j);
else
best(i,j)=MAX{best(i-1,j-need[i])+value[i],best(i-1,j)};
這就是從第i階段到第i-1階段的狀態轉移規律,程序員為了把逼格提高,起了一個術語——狀態轉移方程.
而當i=0時**,只需設置一下邊界值best(0,j)=0.這樣,求解best(N,V)這個看起來很復雜又無從下手的問題,就變成了從i=0時的best(0,j)=0逐漸到i=N時的best(N,j).
*best(N,V)只是物品、背包容量和價值三者之間的關系表示,千萬不要糾結它為什麼這麼表示,到底什麼意思,裡面又是如何根據N,V來得到價值的;
**本來i=0是沒有意義的,因為是從第N個物品逐漸推導到第1個物品,設置i=0時的best(i,j)只是為了滿足數學上的計算;
代碼實現:舉一個實例助於理解,現有4個物品,編號1、2、3、4;他們所需空間分別為2、3、4、1,而各自價值為2、5、3、2,背包總空間為5,該怎樣放才能使得背包內物品價值最大呢?根據狀態轉移方程,列表如下所示:
i need value j 1 2 3 4 5 0 0 0 0 0 0 1 2 2 2 3 5 3 4 3 4 1 2
j從1遞增到5,best(1,1)=best(0,1)=0,依次求best(i,j)並填入表中,得:
i need value j 1 2 3 4 5 1 2 2 0 2 2 2 2
i從1到4,填完整個表格:
i need value j 1 2 3 4 5 0 0 0 0 0 0 1 2 2 0 2 2 2 2 2 3 5 0 2 5 5 7 3 4 3 0 2 5 5 7 4 1 2 2 2 5 7 7
觀察表格,同樣是一個二維的數組,直觀上看數塔是從下往上階段遞推,01背包是一行一行向數組最右下角遞推.定義二維數組best[N+1][V],best[N+1][V]就是全局最優解.核心代碼如下:
for(j=1;j<=V;j++)
best[0][j]=0;
for(i=1;i<=N+1;i++)
for(j=1;j<=V;j++)
{
if(j<need[i])
best[i][j]=best[i-1][j];
else
best[i][j]=MAX{best[i-1][j-need[i]]+value[i],best[i-1][j]};
}
代碼優化:如果覺得問題就這麼解決,那就沒意思了.在上述表格中,其實可以發現,為了得到最後的一個元素,申請一個龐大的(N+1)*V的數組過於鋪張浪費了,用ACMer的話來說就是所需存儲空間過大.不難發現,求解第i階段其實只需要第i-1階段的值,也就是說,無論N有多大,只需要一個2*V的數組就可以解決問題了,這樣確實可以省下不少空間.i為偶數存入best[0][],i為奇數存入best[1][].
best(i-1,j-x)
...
best(i-1,j)
...
best(i,j)
for(j=1;j<=V;j++)
best[0][j]=0;
for(i=1;i<=N+1;i++)
{
if(i%2){
if(j<need[i])
best[1][j]=best[0][j];
else
best[1][j]=MAX{best[0,j-need[i]]+value[i],best[0,j]};
}
else{
if(j<need[i])
best[0][j]=best[1][j];
else
best[0][j]=MAX{best[1][j-need[i]]+value[i],best[1][j]};
}
}
繼續優化:看到標題就會猜到,問題還可以繼續簡化成一維數組.至於如何實現呢,看上述表格繼續思考(畫個表格不是用來占空間的.
...
best(j-2)
best(j-1)
best(j)
...
初始設置一維數組best[]={0},此時要留心兩個細節:
(1)必須從best[V],best[V-1]開始計算並覆蓋原先數據;
(2)只需要覆蓋到j=need[i].
至於原因不難理解,這裡直接給出核心代碼:
__int64 best[]={0}; //long long
for(i=1; i<=n; i++)
for(j=m; j>=needed[i]; j--)
best[j]=MAX{best[j],best[j-need[i]]+value[i]};
優化到現在,也就是說整個01背包問題,只需要三行代碼!無論是時間上,還是空間上,還是代碼的簡潔性,都達到最優!