學過數據結構的都知道樹,那麼什麼是樹?
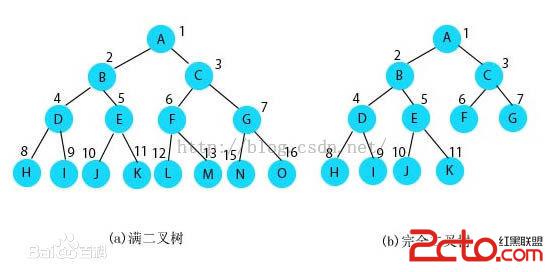
樹(tree)是包含n(n>0)個結點的有窮集,其中: (1)每個元素稱為結點(node); (2)有一個特定的結點被稱為根結點或樹根(root)。 (3)除根結點之外的其余數據元素被分為m(m≥0)個互不相交的集合T1,T2,……Tm-1,其中每一個集合Ti(1<=i<=m)本身也是一棵樹,被稱作原樹的子樹(subtree)。 樹也可以這樣定義:樹是由根結點和若干顆子樹構成的。樹是由一個集合以及在該集合上定義的一種關系構成的。集合中的元素稱為樹的結點,所定義的關系稱為父子關系。父子關系在樹的結點之間建立了一個層次結構。在這種層次結構中有一個結點具有特殊的地位,這個結點稱為該樹的根結點,或稱為樹根。 我們可以形式地給出樹的遞歸定義如下: 單個結點是一棵樹,樹根就是該結點本身。 設T1,T2,..,Tk是樹,它們的根結點分別為n1,n2,..,nk。用一個新結點n作為n1,n2,..,nk的父親,則得到一棵新樹,結點n就是新樹的根。我們稱n1,n2,..,nk為一組兄弟結點,它們都是結點n的子結點。我們還稱T1,T2,..,Tk為結點n的子樹。 空集合也是樹,稱為空樹。空樹中沒有結點。 那麼常見樹的種類有:滿二叉樹,完全二叉樹,二叉樹,紅黑樹,無序樹,哈夫曼樹等等。 今天我們主要是來了解二叉樹,
1、每個節點最多有兩個子節點的樹形結構
2、其中起始節點叫做根節點,除了根節點之外,每個節點有且只有一個父節點
3、沒有任何子節點的節點 叫做葉子節點,除了葉子節點之外,每個節點都可以有兩個子節點
4、除了根節點和葉子節點之外,剩下的節點叫枝節點,枝節點有父節點也有子節點
5、二叉樹中每層節點均達到最大值,並且除了葉子節點之外每個節點都有兩個子節點,叫做滿二叉樹
6、二叉樹中除了最後一層之外,每層節點數均達到最大值,並且最後一層的節點連續集中在左邊,叫完全二叉樹
對於二叉樹的處理采用遞歸的方法:
處理(二叉樹)
{
if(二叉樹為空) 直接處理;
else
{
處理根節點;
處理左子樹;=> 遞歸
處理右子樹;=> 遞歸
}
}
二叉樹的存儲結構
(1)順序存儲結構
從上到下,從左到右,依次存儲每個節點
(2)鏈式存儲結構
每個節點中除了存儲數據元素本身之外,還需要兩指針
如:
typedef struct Node
{
int data;//數據內容
struct Node* left;//指向左子樹
struct Node* right;//指向右子樹
}Node;
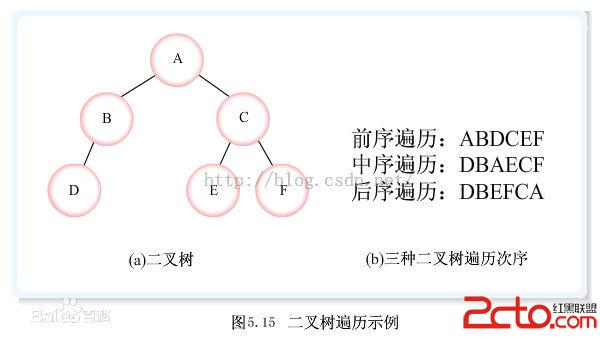
遍歷方式接下來我們來看看二叉樹的各類操作的實現:
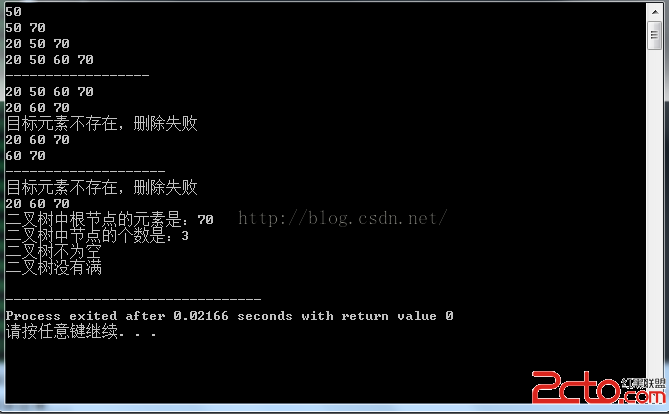
//實現有序二叉樹的各種操作 #include#include //定義節點的數據類型 typedef struct Node { int data;//存儲數據內容 struct Node* left;//左子樹的地址 struct Node* right;//右子樹的地址 }Node; //定義有序二叉樹的數據類型 typedef struct { Node* root;//記錄根節點的地址 int cnt;//記錄節點的個數 }Tree; //實現向有序二叉樹中插入新節點的操作 void insert_data(Tree* pt,int data); //插入新節點的遞歸函數 void insert(Node** pRoot,Node* pn); //采用中序遍歷方法進行遍歷 void travel_data(Tree* pt); //遍歷的遞歸函數 void travel(Node* pRoot); //實現創建新節點 Node* create_node(int data); //實現清空樹中的所有節點 void clear_data(Tree* pt); //實現清空的遞歸函數 void clear(Node** pRoot); //實現查找一個指定的節點 Node** find_data(Tree* pt,int data); //查找的遞歸函數 Node** find(Node** pRoot,int data); //實現刪除指定的節點 void del_data(Tree* pt,int data); //修改指定元素的操作 void modify(Tree* pt,int data,int new_data); //判斷二叉樹是否為空 int empty(Tree* pt); //判斷二叉樹是否為滿 int full(Tree* pt); //計算二叉樹中節點的個數 int size(Tree* pt); //獲取根節點的元素值 int get_root(Tree* pt); int main(void) { //創建有序二叉樹,並且進行初始化 Tree tree; tree.root = NULL; tree.cnt = 0; //插入新節點,進行遍歷 insert_data(&tree,50); travel_data(&tree);//50 insert_data(&tree,70); travel_data(&tree);//50 70 insert_data(&tree,20); travel_data(&tree);//20 50 70 insert_data(&tree,60); travel_data(&tree);//20 50 60 70 printf("------------------\n"); //clear_data(&tree); travel_data(&tree);//20 50 60 70 del_data(&tree,50); travel_data(&tree);//20 60 70 del_data(&tree,30);//刪除失敗 travel_data(&tree);//20 60 70 del_data(&tree,20); travel_data(&tree);//60 70 printf("--------------------\n"); modify(&tree,10,20);//插入20 travel_data(&tree);//20 60 70 printf("二叉樹中根節點的元素是:%d\n",get_root(&tree));//70 printf("二叉樹中節點的個數是:%d\n",size(&tree));//3 printf("%s\n",empty(&tree)?"二叉樹為空":"二叉樹不為空"); printf("%s\n",full(&tree)?"二叉樹已滿":"二叉樹沒有滿"); return 0; } //修改指定元素的操作 //舊元素不存在時,直接插入新元素即可 void modify(Tree* pt,int data,int new_data) { //1.刪除舊元素 del_data(pt,data); //2.插入新元素 insert_data(pt,new_data); } //判斷二叉樹是否為空 int empty(Tree* pt) { return NULL == pt->root; } //判斷二叉樹是否為滿 int full(Tree* pt) { return 0; } //計算二叉樹中節點的個數 int size(Tree* pt) { return pt->cnt; } //獲取根節點的元素值 int get_root(Tree* pt) { if(empty(pt)) { return -1;//表示失敗(以後講到) } return pt->root->data; } //實現刪除指定的節點 void del_data(Tree* pt,int data) { //1.查找目標元素所在節點的地址 Node** pp = find_data(pt,data); //2.判斷查找失敗情況,不需要刪除 if(NULL == *pp) { printf("目標元素不存在,刪除失敗\n"); return; } //3.合並左右子樹,左子樹插入到右子樹中 if((*pp)->left != NULL) { //左子樹不為空時,需要插入到右子樹中 insert(&(*pp)->right,(*pp)->left); } //4.尋找指針記錄要刪除的節點地址 Node* q = *pp; //5.將原來指向要刪除節點的指針 重新指向 合並之後的右子樹 *pp = (*pp)->right; //6.刪除目標元素所在的節點 free(q); q = NULL; //7.節點個數減1 pt->cnt--; } //查找的遞歸函數 Node** find(Node** pRoot,int data) { //1.判斷二叉樹是否為空,為空直接返回 if(NULL == *pRoot) { return pRoot;//&pt->root; } //2.比較根節點元素和目標元素的大小,如果相等,直接返回 if(data == (*pRoot)->data) { return pRoot;//&pt->root; } //3.若目標元素小於根節點元素值,左子樹查找 else if(data < (*pRoot)->data) { return find(&(*pRoot)->left,data); } //4.若目標元素大於根節點元素,去右子樹查找 else { return find(&(*pRoot)->right,data); } } //實現查找一個指定的節點 //返回 指向目標元素所在節點的指針 的地址 Node** find_data(Tree* pt,int data) { //調用遞歸函數實現查找 return find(&pt->root,data); } //實現清空的遞歸函數 void clear(Node** pRoot) { //判斷二叉樹是否為空 if(*pRoot != NULL) { //1.清空左子樹 clear(&(*pRoot)->left); //2.清空右子樹 clear(&(*pRoot)->right); //3.清空根節點 free(*pRoot); *pRoot = NULL; } } //實現清空樹中的所有節點 void clear_data(Tree* pt) { //調用遞歸函數實現清空 clear(&pt->root); //二叉樹的節點個數清零 pt->cnt = 0; } //實現創建新節點 Node* create_node(int data) { Node* pn = (Node*)malloc(sizeof(Node)); pn->data = data; pn->left = NULL; pn->right = NULL; return pn; } //遍歷的遞歸函數 void travel(Node* pRoot) { //判斷二叉樹不為空時才需要遍歷 if(pRoot != NULL) { //1.遍歷左子樹 travel(pRoot->left); //2.遍歷根節點 printf("%d ",pRoot->data); //3.遍歷右子樹 travel(pRoot->right); } } //采用中序遍歷方法進行遍歷 void travel_data(Tree* pt) { //調用遞歸函數進行遍歷 travel(pt->root); //打印換行 printf("\n"); } //插入新節點的遞歸函數 void insert(Node** pRoot,Node* pn) { //1.判斷二叉樹是否為空,如果為空則讓根節點指針直接指向新節點 if(NULL == *pRoot) { *pRoot = pn; return; } //2.如果二叉樹非空,比較根節點和新節點大小 //2.1 如果根節點大於新節點,插入左子樹 if((*pRoot)->data > pn->data) { insert(&(*pRoot)->left,pn); } //2.2 如果根節點小於等於新節點,插入右子樹 else { insert(&(*pRoot)->right,pn); } } //實現向有序二叉樹中插入新節點的操作 void insert_data(Tree* pt,int data) { //1.創建新節點,進行初始化 create_node //Node* pn = (Node*)malloc(sizeof(Node)); //pn->data = data; //pn->left = NULL; //pn->right = NULL; //2.插入新節點到二叉樹中,調用遞歸函數 insert(&pt->root,create_node(data)); //3.二叉樹中節點個數加1 pt->cnt++; }