習題集解析部分
第6章 樹和二叉樹
——《數據結構題集》-嚴蔚敏.吳偉民版
源碼使用說明 鏈接☛☛☛ 《數據結構-C語言版》(嚴蔚敏,吳偉民版)課本源碼+習題集解析使用說明
課本源碼合輯 鏈接☛☛☛ 《數據結構》課本源碼合輯
習題集全解析 鏈接☛☛☛ 《數據結構題集》習題解析合輯
相關測試數據下載 鏈接☛ 數據包
本習題文檔的存放目錄:數據結構\▼配套習題解析\▼06 樹和二叉樹
文檔中源碼的存放目錄:數據結構\▼配套習題解析\▼06 樹和二叉樹\▼習題測試文檔-06
源碼測試數據存放目錄:數據結構\▼配套習題解析\▼06 樹和二叉樹\▼習題測試文檔-06\Data
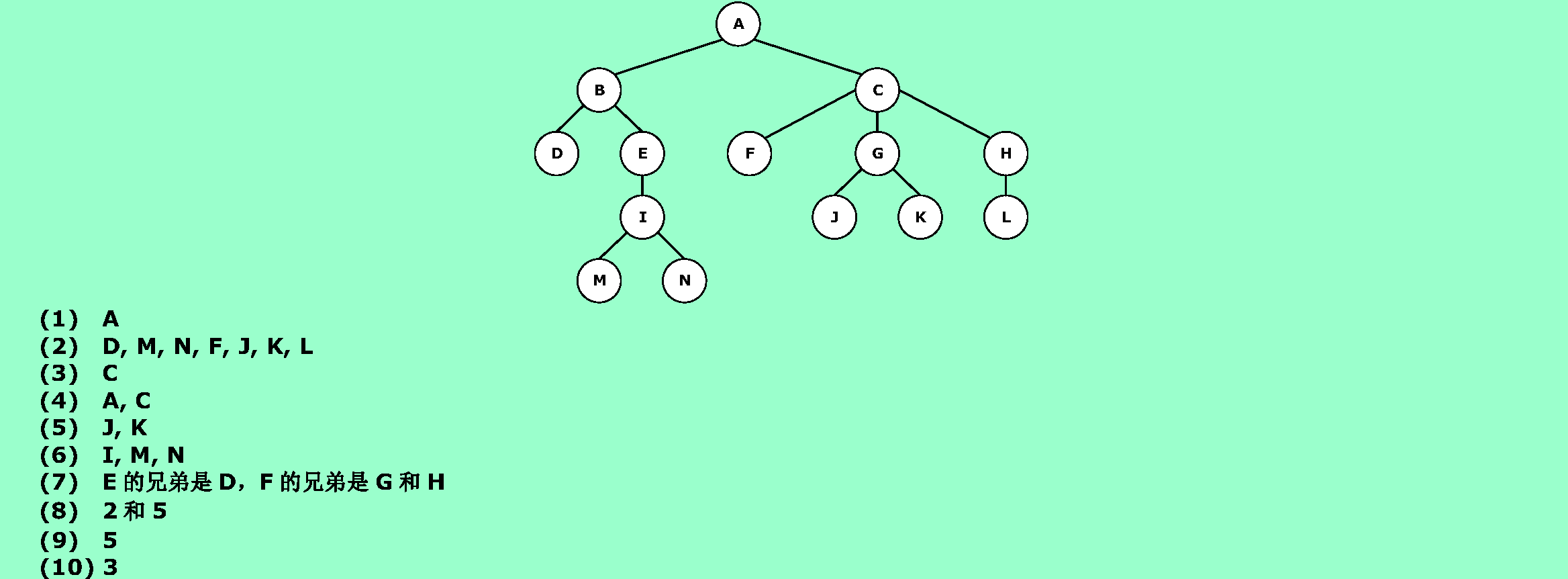
6.1❶已知一棵樹的集合為{<I, M>, <I, N>, <E, I>, <B, E>, <B, D>, <A, B>, <G, J>, <G, K>, <C, G>, <C, F>, <H, L>, <C, H>, <A, C>},請畫出這棵樹,並回答下列問題:
(1)哪個是根結點?
(2)哪些是葉子節點?
(3)哪個是結點G的雙親?
(4)哪些是結點G的祖先?
(5)哪些是結點G的孩子?
(6)哪些是結點E的子孫?
(7)哪些是結點E的兄弟?哪些是結點F的兄弟?
(8)結點B和N的層次號分別是什麼?
(9)樹的深度是多少?
(10)以結點C為根的子樹的深度是多少?
6.2❶一棵度為2的樹與一棵二叉樹有何區別?

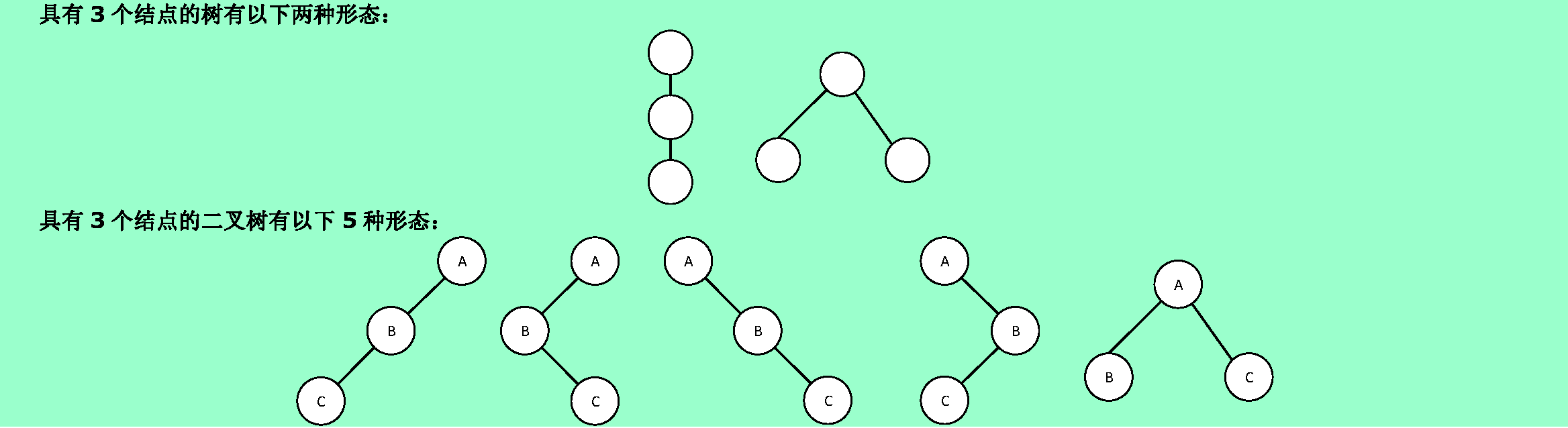
6.3❶試分別畫出具有3個結點的樹和3個結點的二叉樹的所有不同形態。
6.4❸一棵深度為H的滿k叉樹有如下性質:第H層上的結點都是葉子結點,其余各層上每個結點都有k棵非空子樹。如果按層次順序從1開始對全部結點編號,問:
(1)各層的結點數目是多少?
(2)編號為p的結點的父結點(若存在)的編號是多少?
(3)編號為p的結點的第i個兒子結點(若存在)的編號是多少?
(4)編號為p的結點有右兄弟的條件是什麼?其右兄弟的編號是多少?

6.5❷已知一棵深度為k的樹中有n1個度為1的結點,n2個度為2的結點,…,nk個度為k的結點,問該樹中有多少個葉子結點?

6.6❸已知在一棵含有n個結點的樹中,只有度為k的分支結點和度為0的葉子結點。試求該樹含有的葉子結點的書目。
6.7❸ 一棵含有n個結點的k叉樹,可能達到的最大深度和最小深度各為多少?

6.8❹證明:一棵滿k叉樹上的葉子結點數n0和非葉子結點數n1之間滿足以下關系:
n0=(k-1)n1+1。

6.9❷試分別推導含有n個結點和含n0個葉子結點的完全三叉樹的深度H。
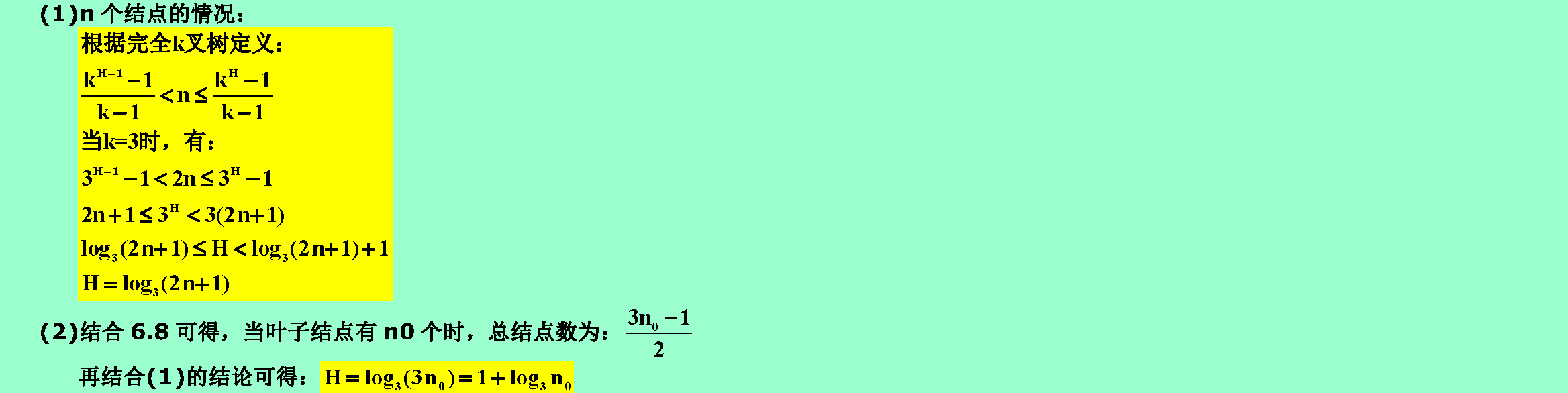
6.10❹對於那些所有非葉子結點均有非空左右子樹的二叉樹:
(1)試問:有n個葉子結點的樹中共有多少個結點?
(2)試證明:
6.11❸在二叉樹的順序存儲結構中,實際上隱含著雙親的信息,因此可和三叉鏈表對應。假設每個指針域占4個字節的存儲,每個信息域占k個字節的存儲。試問:對於一棵有n個結點的二叉樹,且在順序存儲結構中最後一個結點的下標為m,在什麼條件下順序存儲結構比三叉鏈表更節省空間?

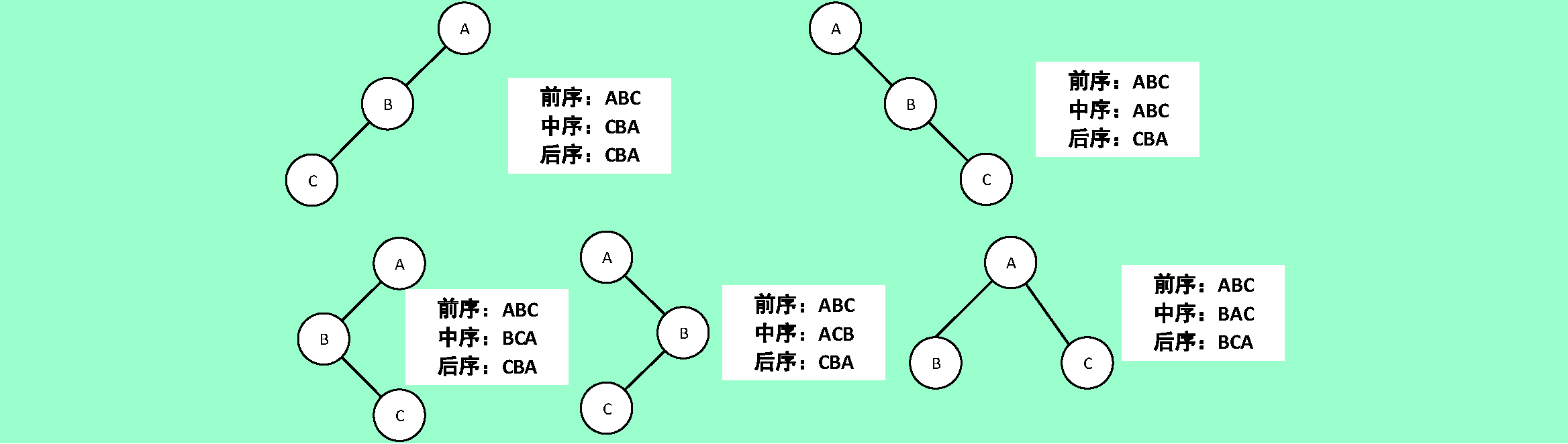
6.12❷ 對題6.3所得各種形態的二叉樹,分別寫出前序、中序和後序遍歷的序列。
6.13❷假設n和m為二叉樹中兩結點,用“1”、“0”或“Φ”(分別表示肯定、恰恰相反或者不一定)填寫下標:

注:如果(1)離a和b最近的共同祖先p存在,且(2)a在p的左子樹中,b在p的右子樹中,則稱a在b的左方(即b在a的右方)。
6.14❷找出所有滿足下列條件的二叉樹:
(a)它們在先序遍歷和中序遍歷時,得到的結點訪問序列相同;
(b)它們在後序遍歷和中序遍歷時,得到的結點訪問序列相同;
(c)它們在先序遍歷和後序遍歷時,得到的結點訪問序列相同。

6.15❷請對下圖所示二叉樹進行後序線索化,為每個空指針建立相應的前驅或後繼線索。

6.16❷將下列二叉鏈表改為先序線索鏈表(不畫出樹的形態)。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
Info
A
B
C
D
E
F
G
H
I
J
K
L
M
N
Ltag
0
0
0
1
0
1
0
1
0
0
1
1
1
1
Lchild
2
4
6
2
7
3
10
14
12
13
13
9
10
11
Rtag
0
0
1
1
0
0
0
1
1
1
0
1
1
1
Rchild
3
5
6
5
8
9
11
3
12
13
14
0
11
8
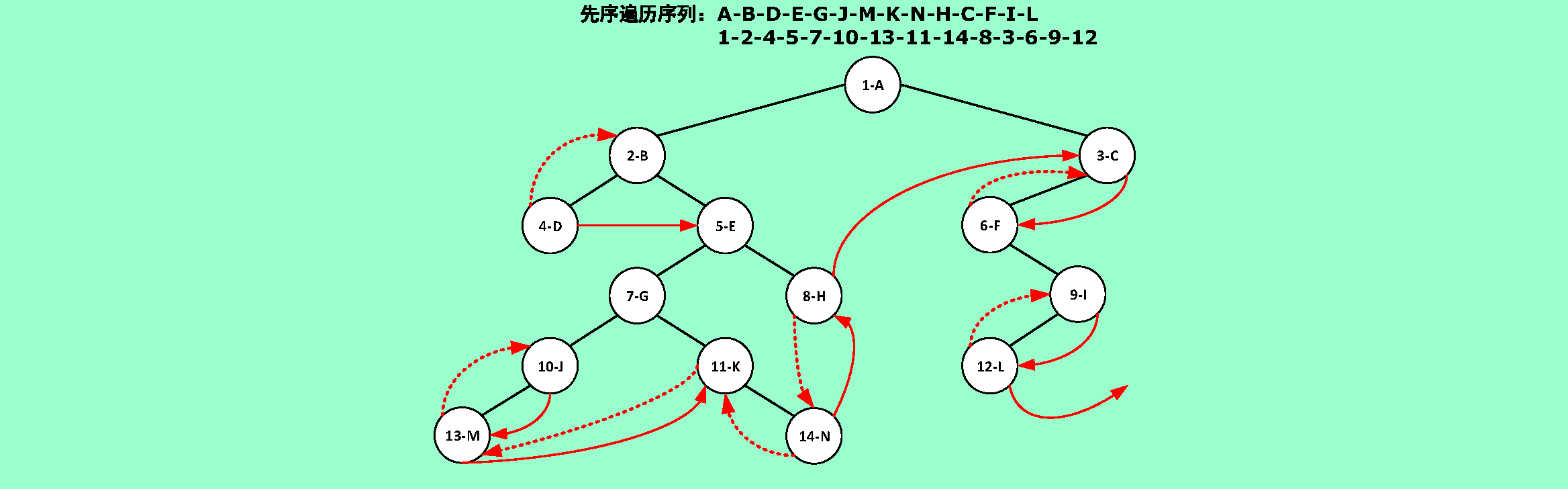
6.17❸閱讀下列算法,若有錯,則改正之。
BiTree InSucc (BiTree q)
{ //已知q是指向中序線索二叉樹上某個結點的指針。
//本函數返回指向*q的後繼的指針。
r = q->rchild;
if(!r->rtag)
while(!r->rtag)
r = r->rchild;
return r;
}//InSucc
6.18❺試討論,能否在一棵中序全線索二叉樹上查找給定結點*p在後序序列中的後繼。

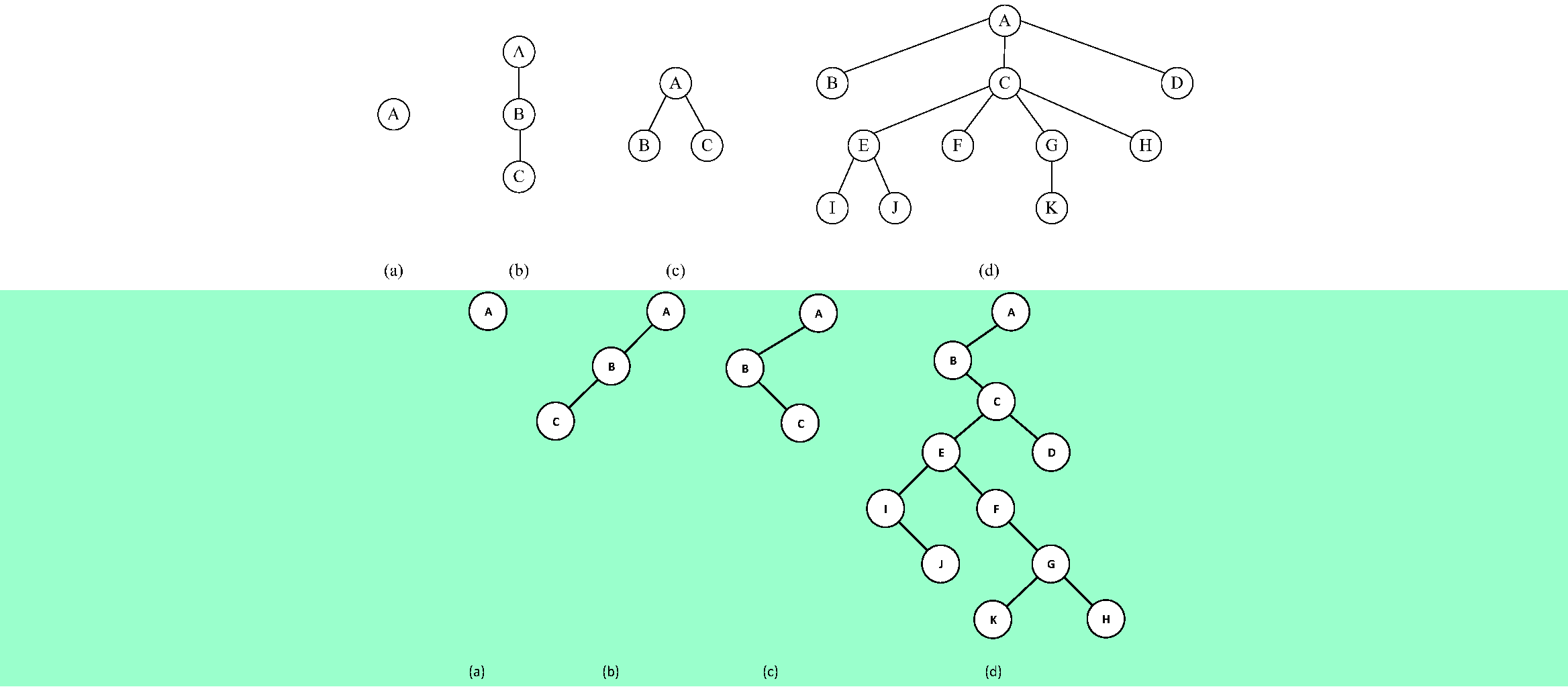
6.19❷ 分別畫出和下列樹對應的各個二叉樹:
6.20❸將下列森林轉換為相應的二叉樹,並分別按以下說明進行線索化:
(1)先序前驅線索化;
(2)中序全線索化前驅線索和後繼線索;
(3)後序後繼線索化。

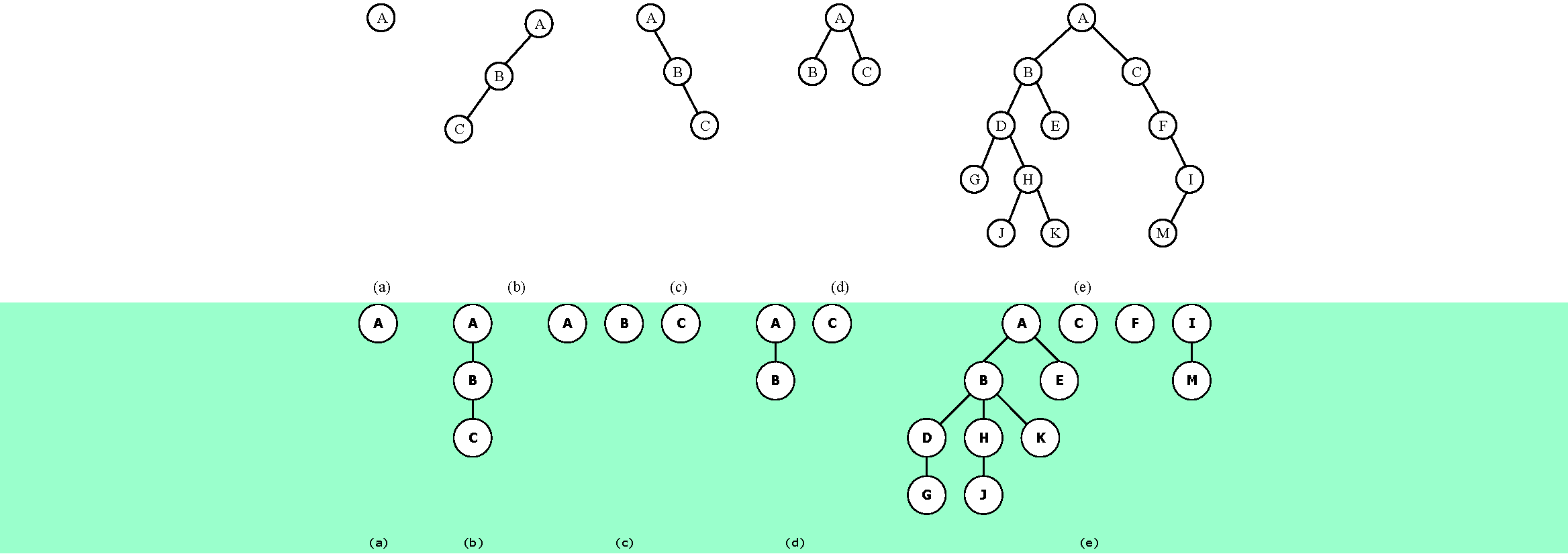
6.21❷畫出和下列二叉樹相應的森林:
6.22❷對於6.19題中給出的各樹分別求出以下遍歷序列:
(1)先根序列;
(2)後根序列。

6.23❷畫出和下列已知序列對應的樹T: 樹的先根次序訪問序列為GFKDAIEBCHJ; 樹的後根次序訪問序列為DIAEKFCJHBG。
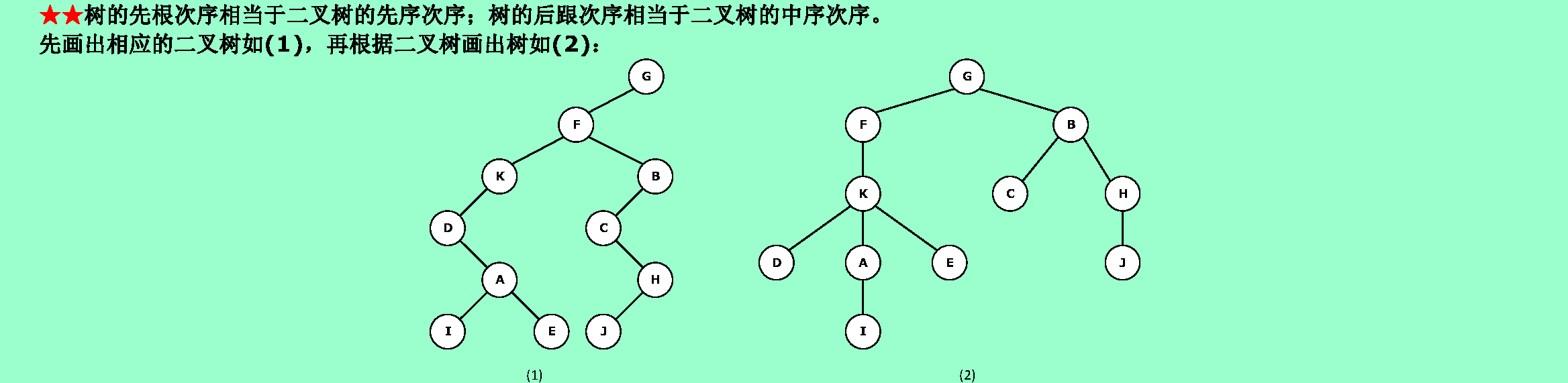
6.24❸畫出和下列已知序列對應的森林F: 森林的先序次序訪問序列為:ABCDEFGHIJKL; 森林的中序次序訪問序列為:CBEFDGAJIKLH。
6.25❸證明:在結點數多於1的哈夫曼樹中不存在度為1的結點。

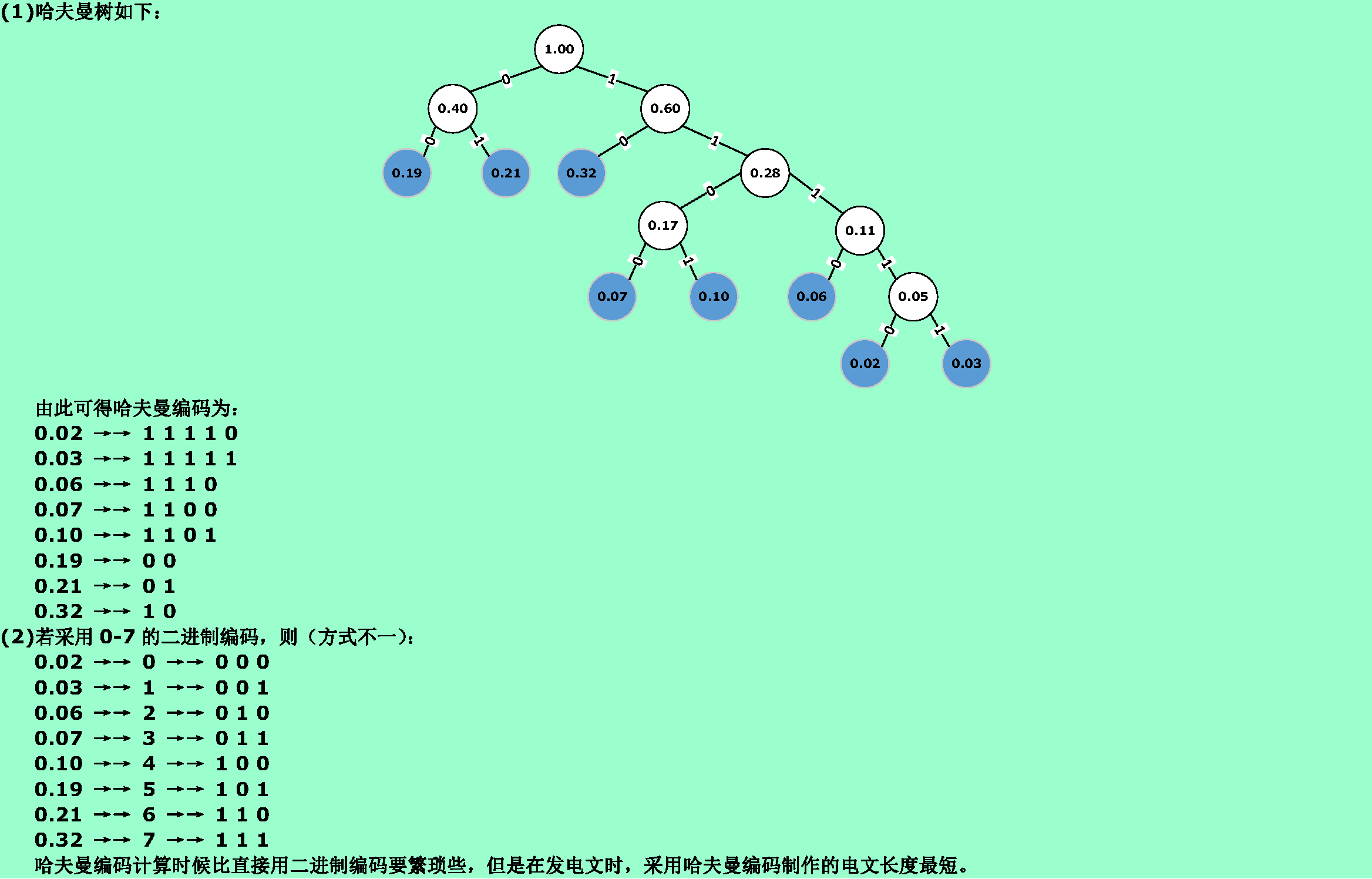
6.26❸假設用於通信的電文僅由8個字母組成,字母在電文中出現的頻率分別為0.07, 0.19, 0.02, 0.06, 0.32, 0.03, 0.21, 0.10。試為這8個字母設計哈夫曼編碼。使用0~7的二進制表示形式是另一種編碼方案。對於上述實例,比較兩種方案的優缺點。
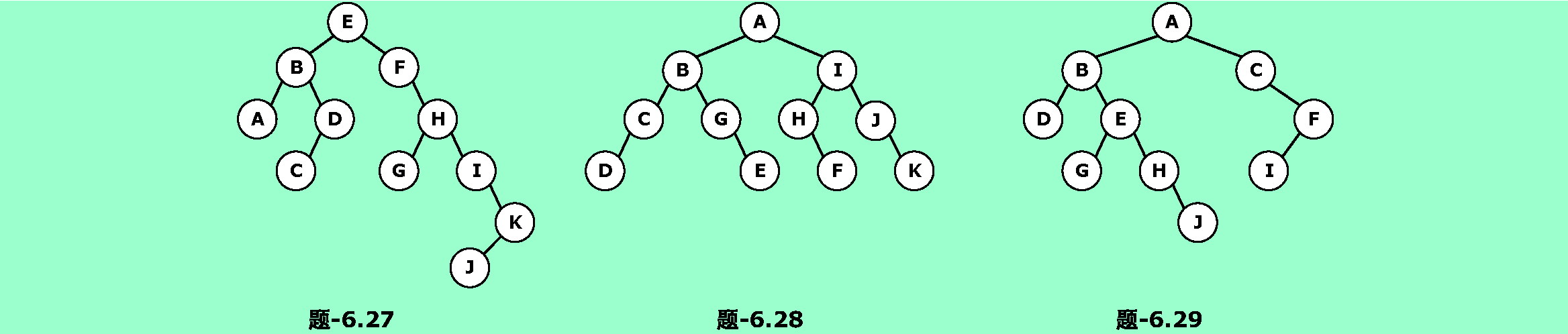
6.27❸假設一棵二叉樹的先序序列為EBADCFHGIKJ和中序序列為ABCDEFGHIJK。請畫出該樹。
6.28❸假設一棵二叉樹的中序序列為DCBGEAHFIJK和後序序列為DCEGBFHKJIA。請畫出該樹。
6.29❸假設一棵二叉樹的層序序列為ABCDEFGHIJ和中序序列為DBGEHJACIF。請畫出該樹。
6.30❹證明:樹中結點u是結點v的祖先,當且僅當在先序序列中u在v之前,且在後序序列中u在v之後。
6.31❹證明:由一棵二叉樹的先序序列和中序序列可唯一確定這課二叉樹。

6.32❺證明:如果一棵二叉樹的先序序列是u1,u2,…,un,中序序列是up1,up2,…,upn,則序列1,2,…,n可以通過一個棧得到序列p1,p2,…,pn;反之,若以上述中的結論作為前提,則存在一棵二叉樹,若其前序序列是u1,u2,…,un,則其中序序列為up1,up2,…,upn。

6.33❸假定用兩個一維數組L[n+1]和R[n+1]作為有n個結點的二叉樹的存儲結構,L[i]和r[i]分別指示結點i(i=1,2,…,n)的左孩子和右孩子,0表示空。試寫一個算法判別結點u是否為結點v的子孫。
6.34❸同6.33題的條件。先由L和R建立一維數組T[n+1],使T中第i(i=1,2,…,n)個分量指示結點i的雙親,然後寫判別結點u是否為結點v的子孫的算法。
6.35❸假設二叉樹中左分支的標號為“0”,右分支的標號為“1”,並對二叉樹增設一個頭結點,令根結點為其右孩子,則從頭結點到樹中任一結點所經分支的序列為一個二進制序列,可認作是某個十進制數的二進制表示。例如,右圖所示二叉樹中,和結點A對應的二進制序列為“110”,即十進制整數6的二進制表示。已知一棵非空二叉樹以順序存儲結構表示,試寫一盡可能簡單的算法,求出與在樹的順序存儲結構中下標值為i的結點對應的十進制整數。

在以下6.36至6.38和6.41至6.53題中,均以二叉鏈表作為二叉樹的存儲結構。 二叉樹的二叉鏈表
6.36❸若已知兩棵二叉樹B1和B2皆為空,或者皆不空且B1的左、右子樹和B2的左、右子樹分別相似,則稱二叉樹B1和B2相似。試編寫算法,判別給定兩棵二叉樹是否相似。
6.37❸試利用棧的基本操作寫出先序遍歷的非遞歸形式的算法。
6.38❹同6.37題條件,寫出後序遍歷的非遞歸算法(提示:為分辨後序遍歷時兩次進棧的不同返回點,需在指針進棧時同時將一個標志進棧)。
6.39❹假設在二叉鏈表的結點中增設兩個域:雙親域(parent)以指示其雙親結點;標志域(mark取值0、1、2)以區分在遍歷過程中到達該結點時應繼續向左或向右或訪問該結點。試以此存儲結構編寫不用棧進行後序遍歷的遞推形式的算法。
6.40❸若在二叉鏈表的結點中只增設一個雙親域以指示其雙親結點,則在遍歷過程中能否不設棧?試以此存儲結構編寫不設棧進行中序遍歷的遞推形式的算法。
6.41❸編寫遞歸算法,在二叉樹中求位於先序序列中第k個位置的結點的值。
6.42❸編寫遞歸算法,計算二叉樹中葉子結點的數目。
6.43❸編寫遞歸算法,將二叉樹中所有結點的左、右子樹相互交換。
6.44❹編寫遞歸算法:求二叉樹中以元素值為x的結點為根的子樹的深度。
6.46❸編寫復制一棵二叉樹的非遞歸算法。
6.47❹編寫按層次順序(同一層自左至右)遍歷二叉樹的算法。
6.48❺已知在二叉樹中,*root為根結點,*p和*q為二叉樹中兩個結點,試編寫求距離它們最近的共同祖先的算法。
6.49❹編寫算法判別給定二叉樹是否為完全二叉樹。
6.50❺假設以三元組(F,C,L/R)的形式輸入一棵二叉樹的諸邊(其中F表示雙親結點的標識,C表示孩子結點標識,L/R表示C為F的左孩子或右孩子),且在輸入的三元組序列中,C是按層次順序出現的。設結點的標識是字符類型。F=‘^’時C為根結點標識,若C也為‘^’,則表示輸入結束。例如,6.15題所示的二叉樹的三元組序列輸入格式為:

試編寫算法,由輸入的三元組序列建立二叉樹的二叉鏈表。
6.51❺編寫一個算法,輸出以二叉樹表示的算術表達式,若該表達式中含有括號,則在輸出時應添上。
6.52❹一棵二叉樹的繁茂度定義為各層結點數的最大值與樹的高度的乘積。試寫一算法,求二叉樹的繁茂度。
6.53❺試編寫算法,求給定二叉樹上從根結點到葉子結點的一條其路徑長度等於樹的深度減一的路徑(即列出從根結點到該葉子結點的結點序列),若這樣的路徑存在多條,則輸出路徑終點(葉子結點)在“最左”的一條。
6.54❸假設以順序表sa表示一棵完全二叉樹,sa.elem[1..sa.last]中存放樹中各結點的數據元素。試編寫算法由此順序存儲結構建立該二叉樹的二叉鏈表。
6.55❹為二叉鏈表的結點增加DescNum域。試編寫一算法,求二叉樹的每個結點的子孫數目並存入其DescNum域。請給出算法的時間復雜度。
6.56❸試寫一個算法,在先序後繼線索二叉樹中,查找給定結點*p在先序序列中的後繼(假設二叉樹的根結點未知)。並討論實現此算法對存儲結構有何要求?
6.57❸試寫一個算法,在後序後繼線索二叉樹中,查找給定結點*p在後序序列中的後繼(二叉樹的根結點指針並未給出)。並討論實現此算法對存儲結構有何要求?

6.58❹試寫一個算法,在中序全線索二叉樹的結點*p之下,插入一棵以結點*x為根、只有左子樹的中序全線索二叉樹,使*x為根的二叉樹稱為*p的左子樹。若*p原來有左子樹,則令它為*x的右子樹。完成插入之後的二叉樹應保持全線索化特性。
6.59❸編寫算法完成下列操作:無重復地輸出以孩子-兄弟鏈表存儲的樹T中所有的邊。輸出的形式為(k1, k2), …, (ki, kj), …,其中,ki和kj為樹結點中的結點標識。
6.60❸試編寫算法,對一棵以孩子-兄弟鏈表表示的樹統計葉子的個數。
6.61❸試編寫算法,求一棵以孩子-兄弟鏈表表示的樹的度。
6.62❹對以孩子-兄弟鏈表表示的樹編寫計算樹的深度的算法。
6.63❸對以孩子鏈表表示的樹編寫計算樹的深度的算法。
6.64❹對以雙親表表示的樹編寫計算樹的深度的算法。


6.65❹已知一棵二叉樹的前序序列和中序序列分別存於兩個一維數組中,試編寫算法建立該二叉樹的二叉鏈表。
6.66❹假設有n個結點的樹T采用了雙親表示法,寫出由此建立樹的孩子-兄弟鏈表的算法。
6.67❹假設以二元組(F,C)的形式輸入一棵樹的諸邊(其中F表示雙親結點的標識,C表示孩子結點標識),且在輸入的二元組序列C中,C是按層次順序出現的。F=‘^’時C為根結點標識,若C也為‘^’,則表示輸入結束。例如,如下所示樹的輸入序列為:

試編寫算法,由輸入的二元組序列建立該樹的孩子-兄弟鏈表。
6.68❸已知一棵樹的由根至葉子結點按層次輸入的結點序列及每個結點的度(每層中自左至右輸入),試寫出構造此樹的孩子-兄弟鏈表的算法。
6.69❹假設以二叉鏈表存儲的二叉樹中,每個結點所含數據元素均為單字母,試編寫算法,按樹形狀打印二叉樹的算法。例如:左下二叉樹印為右下形狀。
6.70❺如果用大寫字母標識二叉樹結點,則一棵二叉樹可以用符合下面語法圖的字符序列表示。試寫一個遞歸算法,由這種形式的字符序列,建立相應的二叉樹的二叉鏈表存儲結構。

例如:6.39題所示的二叉樹輸入形式為A(B(#,D),C(E(#,F),#))。
6.71❺假設樹上每個結點所含的數據元素為一個字母,並且以孩子-兄弟鏈表為樹的存儲結構,試寫一個按凹入表方式打印一棵樹的算法。例如:左下所示樹印為右下形狀。
6.72❺以孩子鏈表為樹的存儲結構,重做6.71題。 孩子-兄弟鏈表
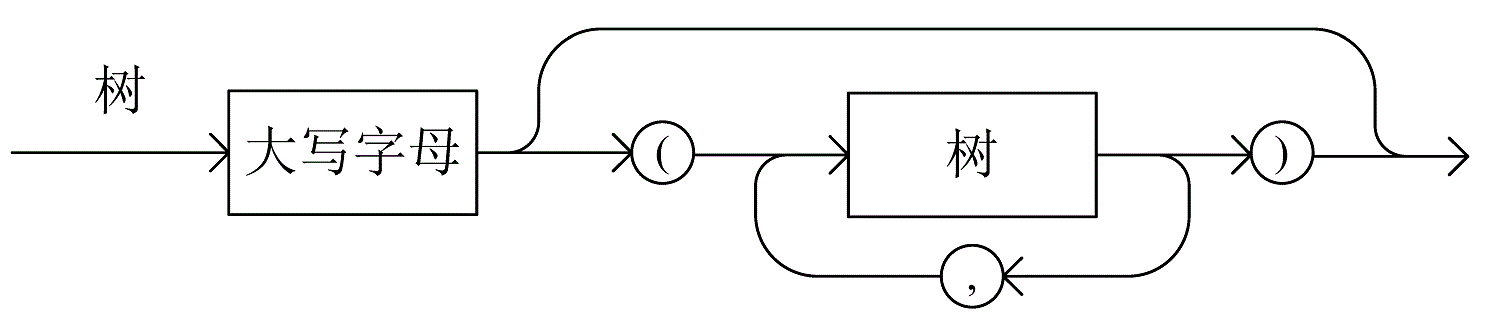
6.73❺若用大寫字母標識樹的結點,則可用帶標號的廣義表形式表示一棵樹,其語法圖如下所示:
例如,6.71題中的樹可用下列形式的廣義表表示:
A(B(E,F),C(G),D)
試寫一遞歸算法,由這種廣義表表示的字符序列構造樹的孩子-兄弟鏈表(提示:按照森林和樹相互遞歸的定義寫兩個互相遞歸調用的算法,語法圖中一對圓括號內的部分可看成為森林的語法圖)。
6.74❺試寫一遞歸算法,以6.73題給定的樹的廣義表表示法的字符序列形式輸出以孩子-兄弟鏈表表示的樹。
6.75❺試寫以遞歸算法,由6.73題定義的廣義表表示法的字符序列,構造樹的孩子鏈表。
6.76❺試寫以遞歸算法,以6.73題給定的樹的廣義表表示法的字符序列形式輸出以孩子鏈表表示的樹。