習題集解析部分
第3章 棧和隊列
——《數據結構題集》-嚴蔚敏.吳偉民版
源碼使用說明 鏈接☛☛☛ 《數據結構-C語言版》(嚴蔚敏,吳偉民版)課本源碼+習題集解析使用說明
課本源碼合輯 鏈接☛☛☛ 《數據結構》課本源碼合輯
習題集全解析 鏈接☛☛☛ 《數據結構題集》習題解析合輯
本習題文檔的存放目錄:數據結構\▼配套習題解析\▼03 棧和隊列
文檔中源碼的存放目錄:數據結構\▼配套習題解析\▼03 棧和隊列\▼習題測試文檔-03
源碼測試數據存放目錄:數據結構\▼配套習題解析\▼03 棧和隊列\▼習題測試文檔-03\Data
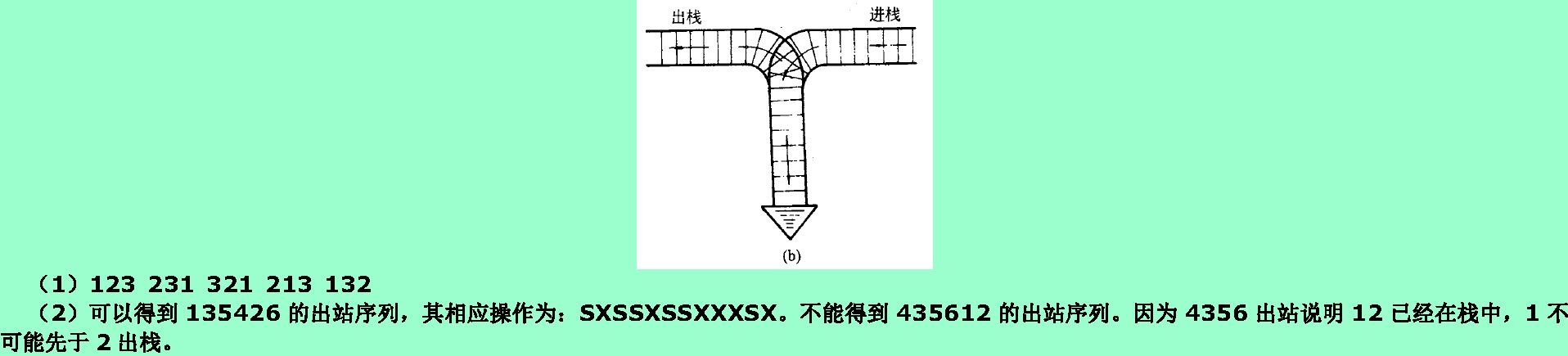
3.1❶若按教科書3.1.1節中圖3.1(b)所示鐵道進行車廂調度(注意:兩側鐵道均為單向行駛道),則請回答:
(1) 如果進站的車廂序列為123,則可能得到的出站車廂序列是什麼?
(2) 如果進站的車廂序列為123456,則能否得到435612和135426的出站序列,並請說明為什麼不能得到或者如何得到(即寫出以‘S’表示進棧和以‘X’表示出棧的棧操作序列)。
3.2❶簡述棧和線性表的差別。

3.3❷寫出下列程序段的輸出結果(棧的元素類型SElemType為char)。
void main()
{
Stack S;
char x, y;
InitStack(S);
x = ’c’; y = ’k’;
Push(S, x); Push(S, ‘a’); Push(S, y); Pop(S, x);
Push(S,‘t’); Push(S, x); Pop(S, x); Push(S,‘s’);
while(!StackEmpty(S))
{
Pop(S,y);
printf(y);
}
printf(x);
}

3.4❷簡述以下算法的功能(棧的元素類型SElemType為int)。
(1)status algo1(Stack S)
{
int i, n, A[255];
n=0;
while(!StackEmpty(S))
{
n++; Pop(S, A[n]);
}
for(i=1; i<=n; i++)
Push(S, A[i]);
}
(2)status algo2(Stack S,int e)
{
Stack T; int d;
InitStack(T);
while(!StackEmpty(S))
{
Pop(S, d);
if(d!=e)
Push(T, d);
}
while(!StackEmpty(T))
{
Pop(T, d);
Push(S, d);
}
}

3.5❹假設以S和X分別表示入棧和出棧的操作,則初態和終態均為空棧的入棧和出棧的操作序列可以表示為僅由S和X組成的序列。稱可以操作的序列為合法序列(例如,SXSX為合法序列,SXXS為非法序列)。試給出區分給定序列為合法序列或非法序列的一般准則,並證明:兩個不同的合法(棧操作)序列(對同一輸入序列)不可能得到相同的輸出元素(注意:在此指的是元素實體,而不是值)序列。

3.6❹ 試證明:若借助棧由輸入序列12…n得到的輸出序列為p1p2…pn(它是輸入序列的一個排列),則在輸出序列中不可能出現這樣的情形:存在著i<j<k使pj<pk<pi。
3.7❹按照四則運算加、減、乘、除和冪運算(↑)優先關系的慣例,並仿照教科書3.2節例3-2的格式,畫出對下列算術表達式求值時操作數棧和運算符棧的變化過程:
A-B×C/D+E↑F

3.8❸試推導求解n階梵塔問題至少要執行的move操作的次數。
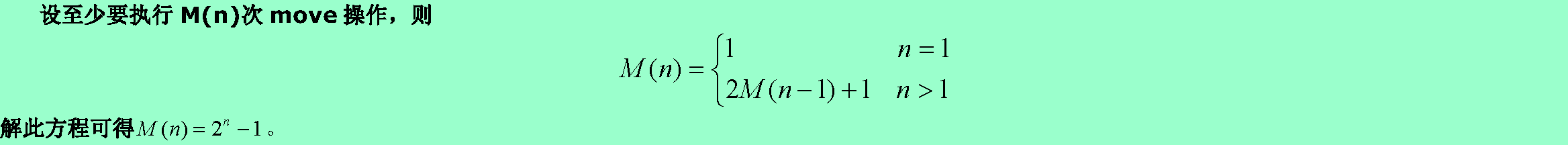
3.9❸試將下列遞推過程改寫為遞歸過程。
void ditui(int n)
{
int i;
i = n;
while(i>1)
cout<<i--;
}

3.10❸試將下列遞歸過程改寫為非遞歸過程。
void test(int &sum)
{
int x;
cin>>x;
if(x==0)
sum=0;
else
{
test(sum);
sum+=x;
}
cout<<sum;
}

3.11❸簡述隊列和堆棧這兩種數據類型的相同點和差異處。

3.12❸寫出以下程序段的輸出結果(隊列中的元素類型QElemType為char)。
void main()
{
Queue Q;
InitQueue(Q);
char x= ‘e’, y= ‘c’;
EnQueue(Q, ‘h’);
EnQueue(Q, ‘r’);
EnQueue(Q, y);
DeQueue(Q, x);
EnQueue(Q, x);
DeQueue(Q, x);
EnQueue(Q, ‘a’);
While(!QueueEmpty(Q))
{
DeQueue(Q,y);
cout<<y;
}
cout<<x;
}

3.13❷簡述以下算法的功能(棧和隊列的元素類型均為int)。
void algo3(Queue &Q)
{
Stack S;
int d;
InitStack(S);
while(!QueueEmpty(Q))
{
DeQueue(Q, d);
Push(S, d);
}
while(!StackEmpty(S))
{
Pop(S, d);
EnQueue(Q, d);
}
}

3.14❹若以1234作為雙端隊列的輸入序列,試分別求出滿足以下條件的輸出序列:
(1) 能由輸入受限的雙端隊列得到,但不能由輸出受限的雙端隊列得到的輸出序列。
(2) 能由輸出受限的雙端隊列得到,但不能由輸入受限的雙端隊列得到的輸出序列。
(3) 既不能由輸入受限的雙端隊列得到,也不能由輸出受限的雙端隊列得到的輸出序列。

3.15❸假設以順序存儲結構實現一個雙向棧,即在一維數組的存儲空間中存在著兩個棧,它們的棧底分別設在數組的兩個端點。試編寫實現這個雙向棧tws的三個操作:初始化inistack(tws)、入棧push(tws,i,x)和出棧pop(tws,i)的算法,其中i為0或1,用以分別指示設在數組兩端的兩個棧,並討論按過程(正/誤狀態變量可設為變參)或函數設計這些操作算法各有什麼有缺點。
3.16❷假設如題3.1所屬火車調度站的入口處有n節硬席或軟席車廂(分別以H和S表示)等待調度,試編寫算法,輸出對這n節車廂進行調度的操作(即入棧或出棧操作)序列,以使所有的軟席車廂都被調整到硬席車廂之前。
3.17❸試寫一個算法,識別一次讀入的一個以@為結束符的字符序列是否為形如‘序列1&序列2’模式的字符序列。其中序列1和序列2中都不含字符‘&’,且序列2是序列1的逆序列。例如,‘a+b&b+a’是屬該模式的字符序列,而‘1+3&3-1’則不是。
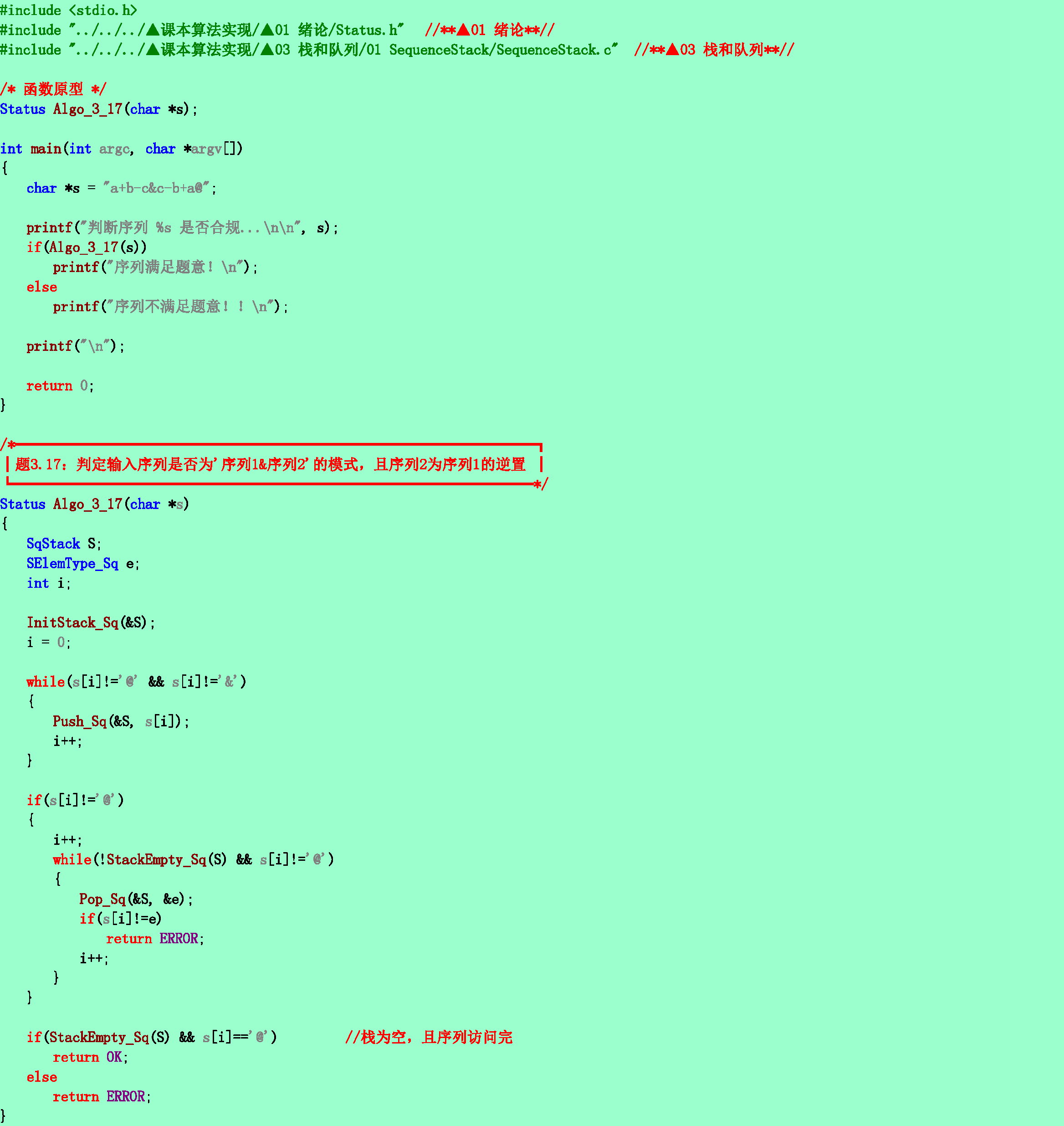
3.18❷試寫一個判別表達式中開、閉括號是否配對出現的算法。
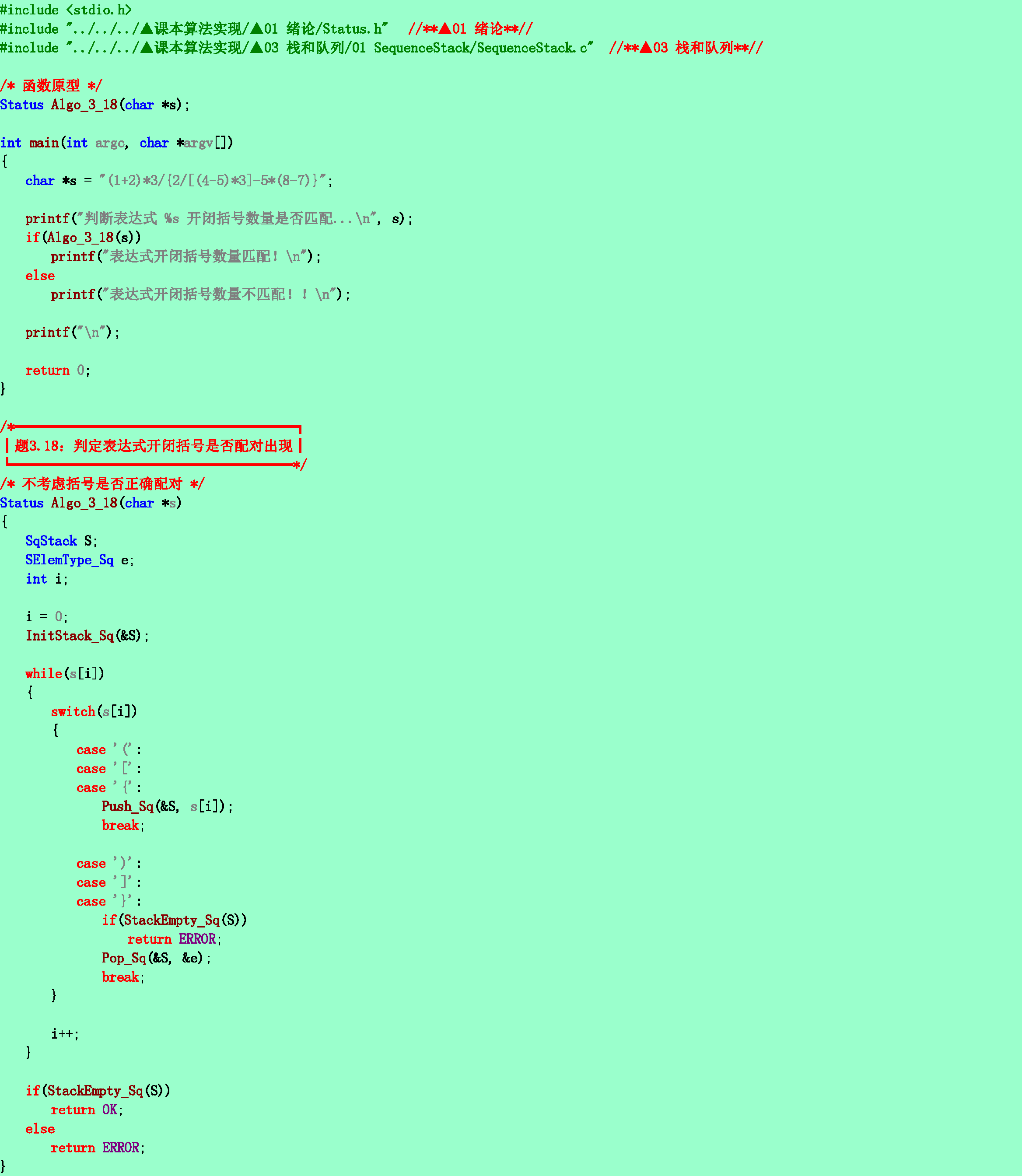
3.19❹假設一個算數表達式中可以包含三種符號:圓括號“(”和“)”、方括號“[”和“]”和花括號“{”和“}”,且這三種括號可按任意的次序嵌套使用(如:…[…{…}…[…]…]…[…]…(…)…)。編寫判別給定表達式中所含括號是否正確配對出現的算法(已知表達式已存入數據元素為字符的順序表中)。
3.20❸假設以二維數組g(1…m, 1…n)表示一個圖像區域,g[i,j]表示該區域中點(i,j)所具顏色,其值為從0到k的整數。編寫算法置換點(i0,j0)所在區域的顏色。約定和(i0,j0)同色的上、下、左、右的鄰接點為同色區域的點。
3.21❸假設表達式有單字母變量(下面算法中將改為只有一位的數字)和雙目四則運算符構成。試寫一個算法,將一個通常書寫形式且書寫正確的表達式轉換為逆波蘭表達式。
3.22❸如題3.21的假設條件,試寫一個算法,對以逆波蘭式表示的表達式求值。
3.23❺如題3.21的假設條件,試寫一個算法,判斷給定的非空後綴表達式是否為正確的逆波蘭表達式,如果是,則將它轉化為波蘭式。
3.24❸試編寫如下定義的遞歸函數的遞歸算法,並根據算法畫出求g(5,2)時棧的變化過程。

3.25❹試寫出求遞歸函數F(n)的遞歸算法,並消除遞歸:
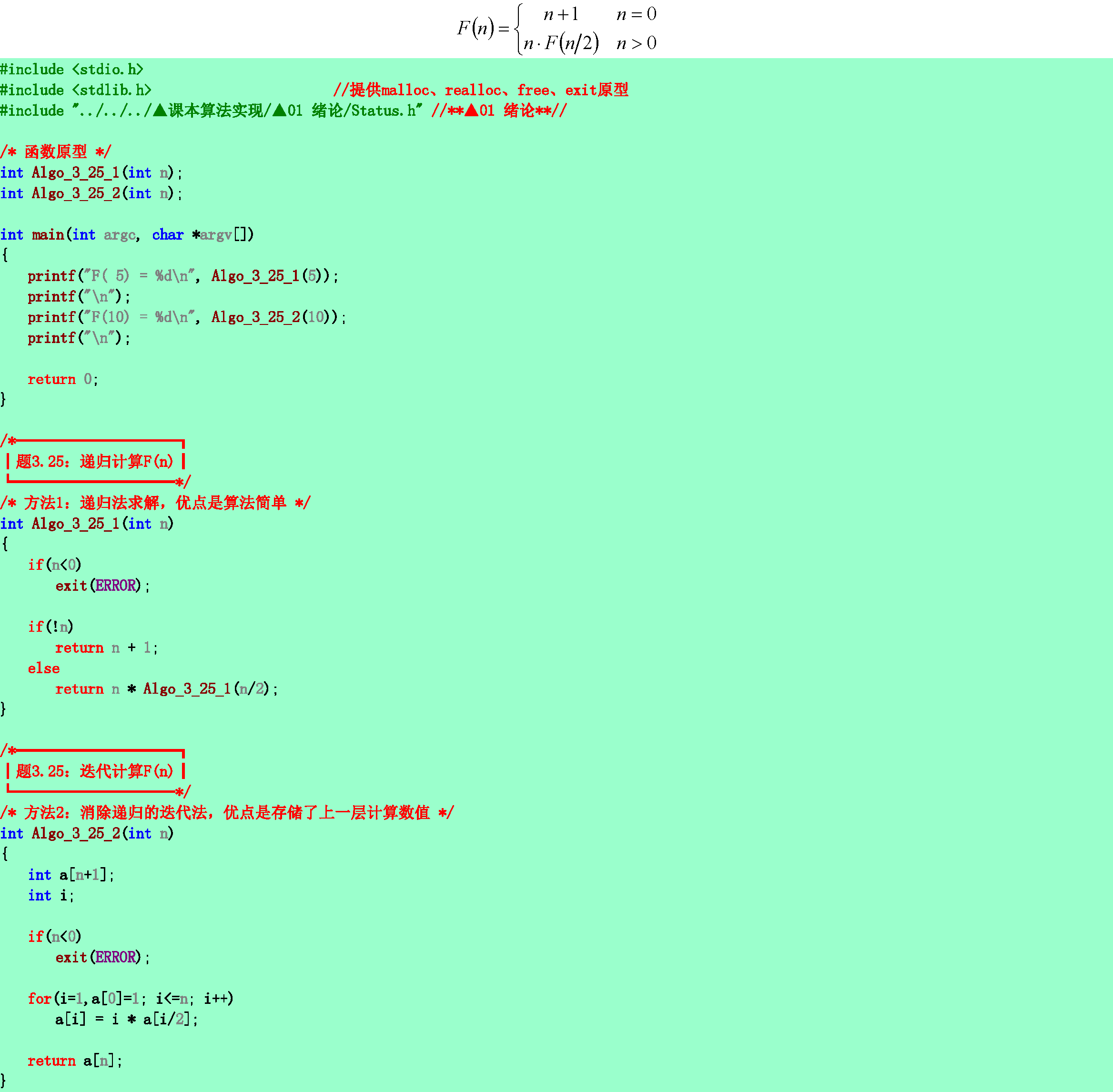
3.26❹求解平方根√A的迭代函數定義如下:
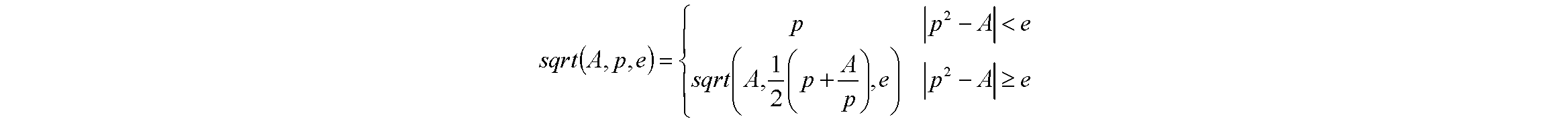
其中,p是A的近似平方根,e是結果允許誤差。試寫出相應的遞歸算法,並消除遞歸。

3.27❺已知Ackerman函數的定義如下:
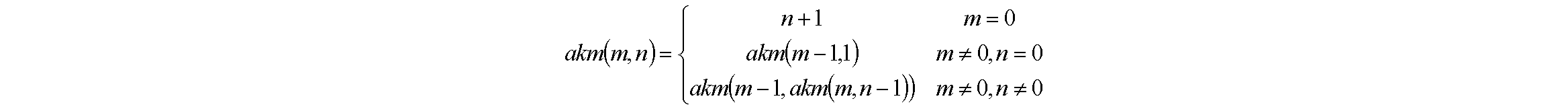
(1) 寫出遞歸算法;
(2) 寫出非遞歸算法;
(3) 根據非遞歸算法,畫出求akm(2,1)時棧的變化過程。
鏈隊
3.28❷假設以帶頭結點的循環鏈表表示隊列,並且只設一個指針指向隊尾元素結點(注意不設頭指針),試編寫相應的隊列初始化、入隊列和出隊列的算法。
順序隊
3.29❸如果希望循環隊列中的元素都能得到利用,則需設置一個標志域tag,並以tag的值為0和1來區分,尾指針和頭指針值相同時的隊列狀態是“空”還是“滿”。試編寫與此結構相應的入隊列和出隊列的算法,並從時間和空間角度討論設標志和不設標志這兩種方法的使用范圍(如當循環隊列容量較小而隊列中每個元素占的空間較多時,哪一種方法較好)。
3.30❷假設將循環隊列定義為:以域變量rear和length分別指示循環隊列中隊尾元素的位置和內含元素的個數。試給出此循環隊列的隊滿條件,並寫出相應的入隊列和出隊列的算法(在出隊列的算法中要返回隊頭元素)。
3.32❹試利用循環隊列編寫求k階菲波那契序列中前n+1項的算法,要求滿足fn≤max而fn+1≥max,其中max為某個約定的常數。(注意:本題所用循環隊列的容量僅為k,則在算法執行結束時,留在循環隊列中的元素應是所求k階菲波那契序列中的最後k項)
3.31❸假設稱正讀和反讀都相同的字符序列為“回文”,例如,‘abba’和‘abcba’是回文,‘abcde’和‘ababab’則不是回文。試寫一個算法判別讀入的一個以‘@’為結束符的字符序列是否是“回文”。
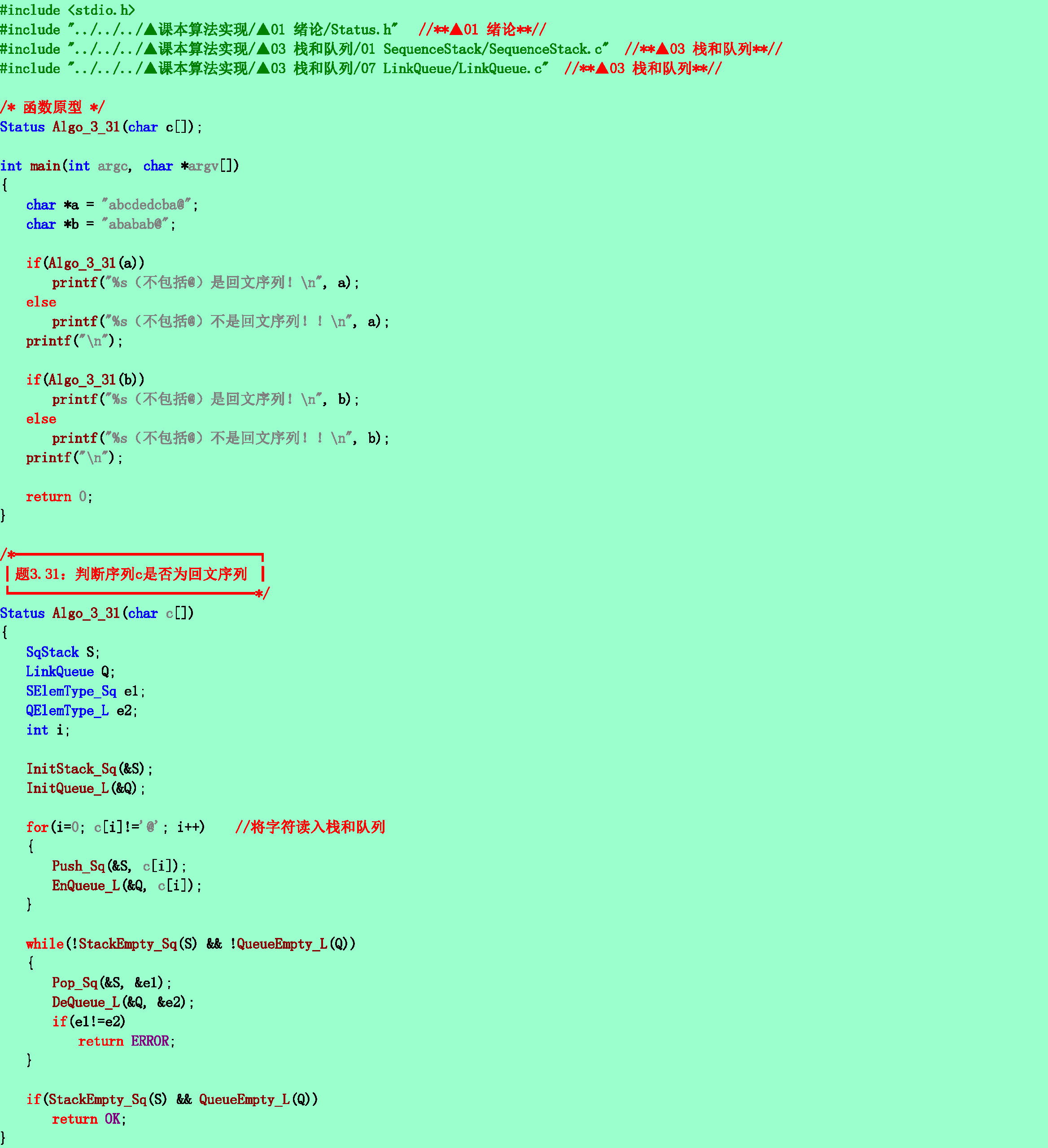
3.33❸在順序存儲結構上實現輸出受限的雙端循環隊列的入列和出列(只允許隊頭出列)算法。設每個元素表示一個待處理的作業,元素值表示作業的預計時間。入隊列采取簡化的短作業優先原則,若一個新提交的作業的預計執行時間小於隊頭和隊尾作業的平均時間,則插入在隊頭,否則插入在隊尾。
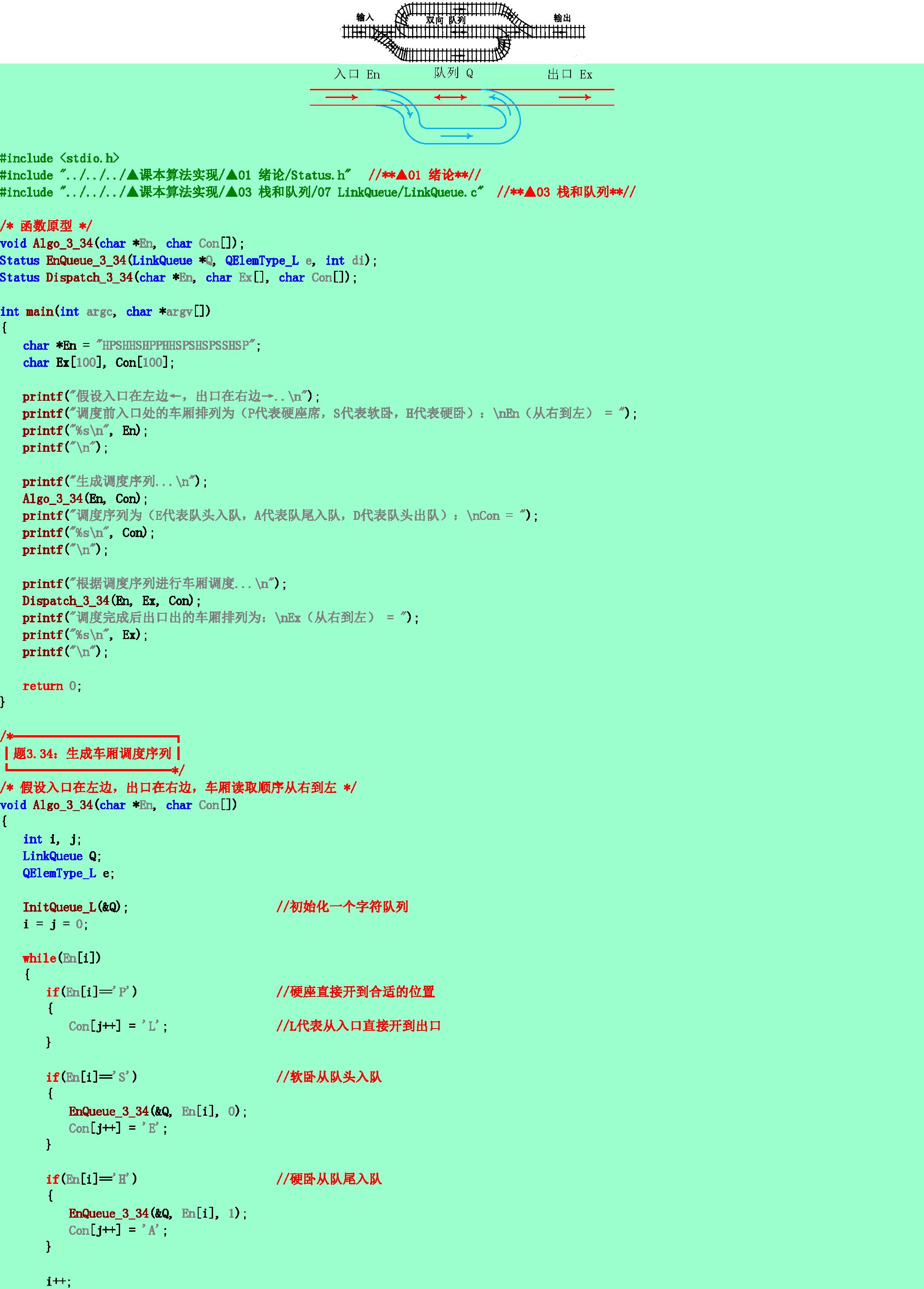
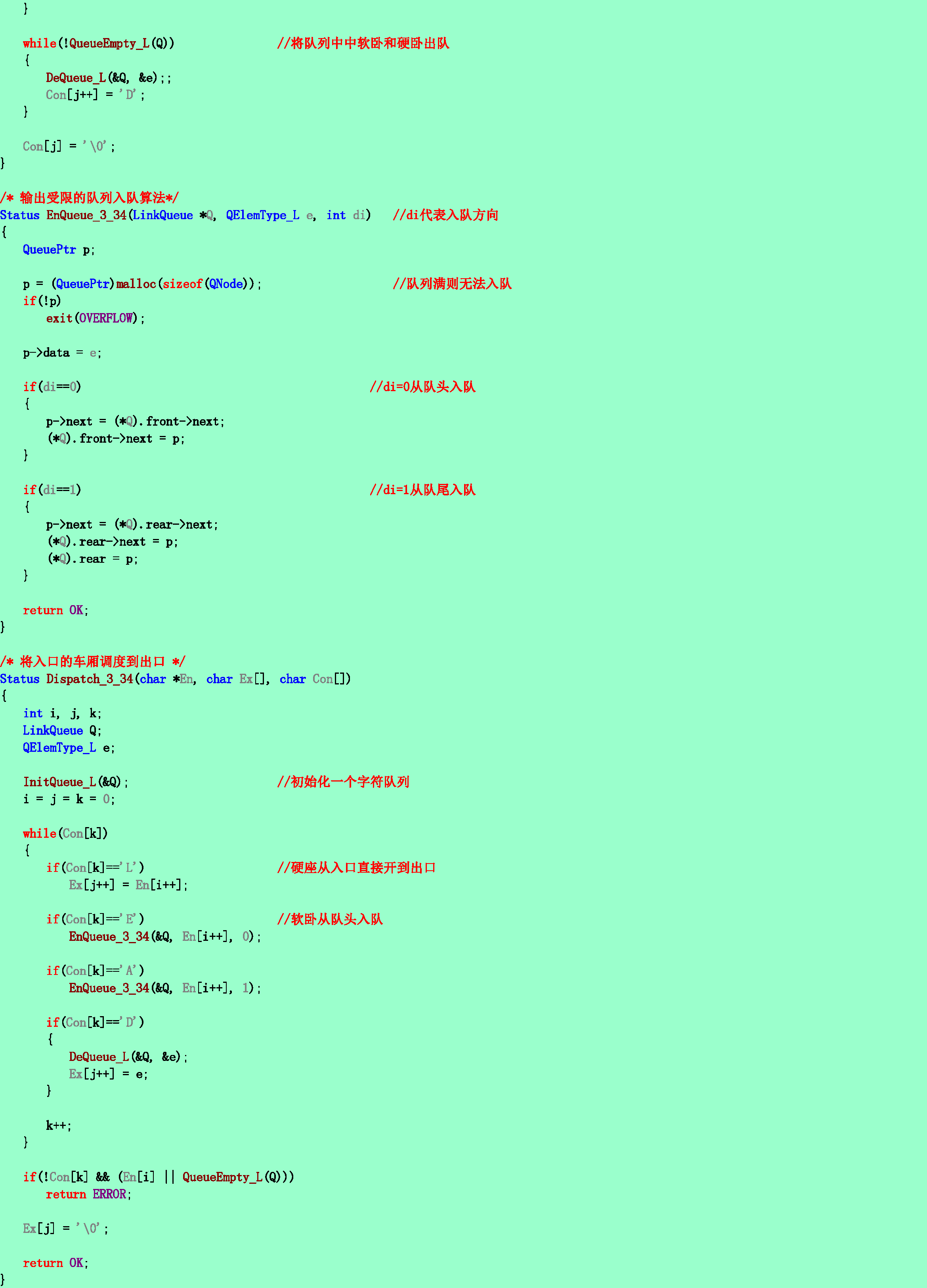
3.34❸假設在如教科書3.4.1節中圖3.9所示的鐵道轉軌網的輸入端有n節車廂:硬座、硬臥和軟臥(分別以P,H和S表示)等待調度,要求這三種車廂在輸出端鐵道上的排列次序為:硬座(P)在前,軟臥(S)在中,硬臥(H)在後。試利用輸出受限(只允許隊頭出列)的雙端隊列對這n節車廂進行調度,編寫算法輸出調度的操作序列:分別以字符‘E’和‘D’表示對雙端隊列的頭端進行入隊列和出隊列的操作;以字符A表示對雙端隊列的尾端進行入隊列的操作。