【數據壓縮】Huffman原理與代碼實現

【數據壓縮】Huffman原理與代碼實現

Huffman算法也是一種無損壓縮算法，但與上篇文章LZW壓縮算法不同，Huffman需要得到每種字符出現概率的先驗知識。通過計算字符序列中每種字符出現的頻率，為每種字符進行唯一的編碼設計，使得頻率高的字符占的位數短，而頻率低的字符長，來達到壓縮的目的。通常可以節省20%~90%的空間，很大程度上依賴數據的特性！Huffman編碼是變長編碼，即每種字符對應的編碼長度不唯一。

前綴碼：任何一個字符的編碼都不是同一字符集中另一種字符編碼的前綴。Huffman編碼為最優前綴碼，即壓縮後數據量最小。

---------------------------------------------------------------------------------------------------------------

Huffman算法：

1.統計字符序列的每種字符的頻率，並為每種字符建立一個節點，節點權重為其頻率；

2.初始化最小優先隊列中，把上述的結點全部插入到隊列中；

3.取出優先隊列的前兩種符號節點，並從優先隊列中刪除；

4.新建一個父節點，並把上述兩個節點作為其左右孩子節點，父節點的權值為左右節點之和；

5.如果此時優先隊列為空，則退出並返回父節點的指針！否則把父節點插入到優先隊列中，重復步驟3；

----------------------------------------------------------------------------------------------------------------

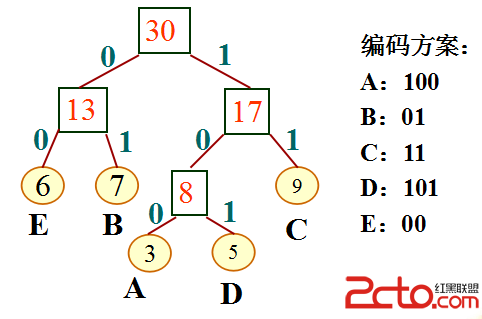
通過上述建造的Huffman樹，可以看到，每種字符結點都是葉子結點，編碼方法：從根節點開始向左定義編碼'0',向右定義為'1',遍歷到葉子結點所得到的二值碼串，即為此種字符的編碼值。由於字符碼字為前綴碼，在譯碼過程中，每種字符可以參照Huffman樹被唯一的譯碼出，但是前綴碼的缺點是，錯誤具有傳播功能，當有1位碼字錯誤，此後的譯碼過程很可能都不正確；

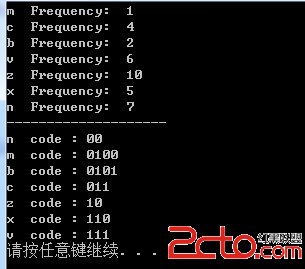
代碼實現：

/*
CSDN 勿在浮沙築高台 
http://blog.csdn.net/luoshixian099
數據壓縮--Huffman編碼 2015年12月21日 
*/
#include 
#include 
#include "compress.h"
using namespace std;
void ShowCode(PNode root, vector &code);
int main()
{
	char A[] = "xxznxznnvvccncvzzbzzvxxczbzvmnzvnnz";//原始數據
	UINT Length = sizeof(A)-1;
	Priority_Q queue(A, Length); //建立優先隊列
	//輸出每組字符的頻率
	for (UINT i = 0; i <= queue.Heap_Size;i++)
	{
		cout << (char)(queue.table[i]->key) << "  Frequency:  " << queue.table[i]->Frequency << endl;
	}
	cout << "--------------------" << endl;
	PNode root = Build_Huffman_Tree(queue);//構建Huffman樹
	vector code;
	ShowCode(root, code); //顯示編碼數據
	return 0;
}
void ShowCode(PNode root,vector &code)
{
   if (root!=NULL)
   {
	   if (root->_left == NULL && root->_right == NULL)  //葉子結點
	   {
		   cout << (char)(root->key) << "  code : " ;
		   for (UINT i = 0; i < code.size() ; i++)
		   {
			   cout << (int)code[i];
		   }
		   cout << endl;
		   return;
	   }
	   code.push_back(0);
	   ShowCode(root->_left,code);
	   code[code.size()-1] = 1;
	   ShowCode(root->_right,code);
	   code.resize(code.size()-1);
   }
}

/*
compress.cpp
*/
#include "compress.h"
Priority_Q::Priority_Q(char *A,int Length) //統計各種字符的頻率
{
	for (int i = 0; i < 256; i++)
	{
		table[i] = new Node;
	}
	Heap_Size = 0;
	for (int i = 0; i < Length; i++)  //統計字符頻率
	{
		bool Flag = true;
		for (int j = 0; j < Heap_Size; j++)
		{
           if ( table[j]->key == *(A+i) )
           {
			   table[j]->Frequency = table[j]->Frequency + 1;
			   Flag = false;
			   break;
           }
		}
		if (Flag)  //加入新的字符
		{
			table[Heap_Size]->key = *(A + i);
			table[Heap_Size]->Frequency = table[Heap_Size]->Frequency + 1;
			Heap_Size++;
		}
	}
	Heap_Size--;
	Build_Min_Heap(Heap_Size); //建立優先隊列
}
void Priority_Q::Build_Min_Heap(UINT Length)
{
	for (int i = (int)(Length / 2); i >= 0; i--)
	{
		Min_Heapify(i);
	}
}
void Priority_Q::Min_Heapify(UINT i)
{
	UINT Smaller = i;
	UINT Left = 2 * i + 1;
	UINT Right = 2 * i + 2;

	if (Left <= Heap_Size && table[Left]->Frequency < table[i]->Frequency)  //判斷是否小於其孩子的值
	{
		Smaller = Left;
	}
	if (Right <= Heap_Size && table[Right]->Frequency < table[Smaller]->Frequency)
	{
		Smaller = Right;
	}
	if (Smaller != i)                      //如果小於，就與其中最大的孩子調換位置
	{
		Swap(i, Smaller);
		Min_Heapify(Smaller);
	}
}
void Priority_Q::Swap(int x, int y) //交換兩個元素的數據
{
	PNode temp = table[x];
	table[x] = table[y];
	table[y] = temp;
}
PNode CopyNode(PNode _src, PNode _dst)//拷貝數據
{
	_dst->Frequency = _src->Frequency;
	_dst->key = _src->key;
	_dst->_left = _src->_left;
	_dst->_right = _src->_right;
	return _dst;
}
PNode Priority_Q::Extract_Min()  //輸出隊列最前結點
{
	if (Heap_Size == EMPTY)
		return NULL;
	if (Heap_Size == 0)
	{
		Heap_Size = EMPTY;
		return table[0];
	}
	if (Heap_Size >= 0)                 
	{
		Swap(Heap_Size, 0);
		Heap_Size--;
		Min_Heapify(0);
	}
	return table[Heap_Size+1];
}
void Priority_Q::Insert(PNode pnode)//優先隊列的插入
{
	Heap_Size++;
	CopyNode(pnode, table[Heap_Size]);
	delete pnode;
	UINT i = Heap_Size;
	while ( i > 0 && table[Parent(i)]->Frequency > table[i]->Frequency )
	{
		Swap(i, Parent(i));
		i = Parent(i);
	}
}
PNode Build_Huffman_Tree(Priority_Q &queue) //建立Huffman樹
{
	PNode parent=NULL,left=NULL,right=NULL;
	while (queue.Heap_Size != EMPTY)
	{
		left = new Node;
		right = new Node;
		parent = new Node;
		CopyNode(queue.Extract_Min(), left); //取出兩個元素
		CopyNode(queue.Extract_Min(), right);
		//復制左右節點數據
		parent->Frequency = right->Frequency + left->Frequency;//建立父節點
		parent->_left = left;
		parent->_right = right;
		if (queue.Heap_Size == EMPTY)
			break;
		queue.Insert(parent);  //再插入回優先隊列
	}
	return parent;
}

/*
compress.h
*/
#ifndef COMPRESS
#define COMPRESS
#include 
#define UINT unsigned int 
#define UCHAR unsigned char 
#define EMPTY 0xFFFFFFFF
#define Parent(i) (UINT)(((i) - 1) / 2)
typedef struct Node   //結點
{
	Node::Node():key(EMPTY), Frequency(0),_left(NULL),_right(NULL){}
	UINT key;
	UINT Frequency;
	struct Node * _left;
	struct Node * _right;
}Node,*PNode;
class Priority_Q  //優先隊列
{
public:
	Priority_Q(char *A, int Length);
	void Insert(PNode pnode); //插入
	PNode Extract_Min();  //取出元素
	UINT Heap_Size;  //隊列的長度
	PNode table[256];  //建立256種結點
private:
	void Build_Min_Heap(UINT Length); //建立隊列
	void Swap(int x, int y);   //交換兩個元素
	void Min_Heapify(UINT i); //維護優先隊列的性質
	
};
PNode Build_Huffman_Tree(Priority_Q &queue);//構建優先隊列
#endif // COMPRESS

http://wenku.baidu.com/view/04a8a13b580216fc700afd2e.html