Description
Examine the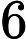 
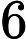checkerboard below and note that the six checkers are arranged on the board so that one and only one is placed in each row and each column, and there is never more than one in any diagonal. (Diagonals run from southeast to northwest and southwest to northeast and include all diagonals, not just the major two.)
1 2 3 4 5 6
-------------------------
1 | | O | | | | |
-------------------------
2 | | | | O | | |
-------------------------
3 | | | | | | O |
-------------------------
4 | O | | | | | |
-------------------------
5 | | | O | | | |
-------------------------
6 | | | | | O | |
-------------------------
The solution shown above is described by the sequence 2 4 6 1 3 5, which gives the column positions of the checkers for each row from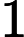 
to :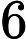
ROW 1 2 3 4 5 6
COLUMN 2 4 6 1 3 5 This is one solution to the checker challenge. Write a program that finds all unique solution sequences to the Checker Challenge (with ever growing values of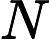 
). Print the solutions using the column notation described above. Print the the first three solutions in numerical order, as if the checker positions form the digits of a large number, and then a line with the total number of solutions.
Input
A single line that contains a single integer (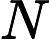
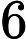
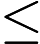
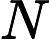
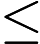
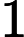
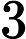) that is the dimension of the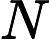 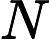checkerboard.
Output
The first three lines show the first three solutions found, presented as 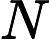numbers with a single space between them. The fourth line shows the total number of solutions found.
Sample Input
6
Sample Output
2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4
題意：N皇後問題，需要輸出前三種排放和可以排放的方式的數量
解題思路：只需要記數輸出三次，其他的和N皇後一樣......（這裡用二維數組來判斷是否同列同斜線...防超時）
代碼如下：
1 #include <stdio.h>
2 int n,t=0,vis[25][25],c[13];
3 void dfs(int cur)
4 {
5 if(cur==n+1)
6 {
7 t++;
8 if(t<4)
9 {
10 for(int i=1; i<=n-1; i++)
11 printf("%d ",c[i]);
12 printf("%d\n",c[n]);
13 }
14 }
15 else
16 {
17 for(int i=1; i<=n; i++)
18 {
19 if(!vis[0][i]&&!vis[1][cur+i]&&!vis[2][cur-i+n]) //判斷是否和前面的皇後沖突
20 {
21 c[cur]=i;
22 vis[0][i]=vis[1][cur+i]=vis[2][cur-i+n]=1;
23 dfs(cur+1);
24 vis[0][i]=vis[1][cur+i]=vis[2][cur-i+n]=0;
25 }
26 }
27 }
28 }
29 int main()
30 {
31 scanf("%d",&n);
32 dfs(1);
33 printf("%d\n",t);
34 return 0;
35 }
