這題是第二次做了,兩次都不是獨立完成,不過我發現我第一次參考的程序,也是參考老師(陳越)的范例做出來的。我對老師給的做了小幅修改,因為我不想有全局變量的的存在,所以我多傳了三個參數進去。正序遍歷每次都是從1到N嗎?看題目我認為應該是,結果我錯了,我是對比正確的程序一點點修改才發現的,不容易啊。下面是題目及程序
1 #include <stdio.h>
2 #include <stdlib.h>
3 #include <string.h>
4
5 typedef struct
6 {
7 int * a;
8 int top;
9 }SeqStack;
10
11 void push(SeqStack * pS, int X);
12 int pop(SeqStack * pS);
13 void solve(int * pre, int * in, int * post, int preL, int inL, int postL, int n);
14
15 int main()
16 {
17 // freopen("in.txt", "r", stdin); // for test
18 int i, N;
19 scanf("%d", &N);
20
21 SeqStack S;
22 S.a = (int *)malloc(N * sizeof(int));
23 S.top = -1;
24 int pre[N], in[N], post[N];
25
26 char chars[5];
27 char * str = chars;
28 int X, pre_index, in_index;
29 pre_index = in_index = 0;
30 for(i = 0; i < 2 * N; i++)
31 {
32 scanf("%s", str);
33 if(strcmp(str, "Push") == 0)
34 {
35 scanf("%d", &X);
36 pre[pre_index++] = X;
37 push(&S, X);
38 }
39 else
40 in[in_index++] = pop(&S);
41 }
42
43 solve(pre, in, post, 0, 0, 0, N);
44 for(i = 0; i < N; i++)
45 {
46 printf("%d", post[i]);
47 if(i < N - 1)
48 printf(" ");
49 else
50 printf("\n");
51 }
52 // fclose(stdin); // for test
53 return 0;
54 }
55
56 void push(SeqStack * pS, int X)
57 {
58 pS->a[++(pS->top)] = X;
59 }
60
61 int pop(SeqStack * pS)
62 {
63 return pS->a[pS->top--];
64 }
65
66 void solve(int * pre, int * in, int * post, int preL, int inL, int postL, int n)
67 {
68 int i, root, L, R;
69
70 if(n == 0)
71 return;
72 if(n == 1)
73 {
74 post[postL] = pre[preL];
75 return;
76 }
77 root = pre[preL];
78 post[postL + n - 1] = root;
79 for(i = 0; i < n; i++)
80 if(in[inL + i] == root)
81 break;
82 L = i;
83 R = n - L - 1;
84 solve(pre, in, post, preL + 1, inL, postL, L);
85 solve(pre, in, post, preL + L + 1, inL + L + 1, postL + L, R);
86 }
An inorder binary tree traversal can be implemented in a non-recursive way with a stack. For example, suppose that when a 6-node binary tree (with the keys numbered from 1 to 6) is traversed, the stack operations are: push(1); push(2); push(3); pop(); pop(); push(4); pop(); pop(); push(5); push(6); pop(); pop(). Then a unique binary tree (shown in Figure 1) can be generated from this sequence of operations. Your task is to give the postorder traversal sequence of this tree.
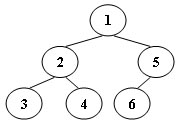
Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (<=30) which is the total number of nodes in a tree (and hence the nodes are numbered from 1 to N). Then 2N lines follow, each describes a stack operation in the format: "Push X" where X is the index of the node being pushed onto the stack; or "Pop" meaning to pop one node from the stack.
Output Specification:
For each test case, print the postorder traversal sequence of the corresponding tree in one line. A solution is guaranteed to exist. All the numbers must be separated by exactly one space, and there must be no extra space at the end of the line.
Sample Input:
6 Push 1 Push 2 Push 3 Pop Pop Push 4 Pop Pop Push 5 Push 6 Pop Pop
Sample Output:
3 4 2 6 5 1