C語言之霍夫曼編碼學習

C語言之霍夫曼編碼學習

?
1，霍夫曼編碼描述
哈夫曼樹─即最優二叉樹，帶權路徑長度最小的二叉樹，經常應用於數據壓縮。 在計算機信息處理中,“哈夫曼編碼”是一種一致性編碼法（又稱“熵編碼法”），用於數據的無損耗壓縮。這一術語是指使用一張特殊的編碼表將源字符（例如某文件中的一個符號）進行編碼。這張編碼表的特殊之處在於，它是根據每一個源字符出現的估算概率而建立起來的（出現概率高的字符使用較短的編碼，反之出現概率低的則使用較長的編碼，這便使編碼之後的字符串的平均期望長度降低，從而達到無損壓縮數據的目的）。這種方法是由David.A.Huffman發展起來的。 例如，在英文中，e的出現概率很高，而z的出現概率則最低。當利用哈夫曼編碼對一篇英文進行壓縮時，e極有可能用一個位(bit)來表示，而z則可能花去25個位（不是26）。用普通的表示方法時，每個英文字母均占用一個字節（byte），即8個位。二者相比，e使用了一般編碼的1/8的長度，z則使用了3倍多。若能實現對於英文中各個字母出現概率的較准確的估算，就可以大幅度提高無損壓縮的比例。

2，問題描述
霍夫曼編碼前首先要統計每個字的字頻，即出現次數，例如：

1、將所有字母出現的次數以從小到大的順序排序，如上圖

2、每個字母都代表一個終端節點（葉節點），比較F.O.R.G.E.T五個字母中每個字母的出現頻率，將最小的兩個字母頻率相加合成一個新的節點。如上圖所示，發現F與O的頻率最小，故相加2+3=5，將F、O組成一個樹，F為左節點，O為右節點，（FO）為根節點，每個節點的取值為其出現頻率（FO的出現頻率為5）

3、比較5.R.G.E.T，發現R與G的頻率最小，故相加4+4=8，將RG組成一個新的節點

4、比較5.8.E.T，發現5與E的頻率最小，故相加5+5=10，因此將FO作為左節點，E作為右節點，FOE作為根節點

5、比較8.10.T，發現8與T的頻率最小，故相加8+7=15，將RG作為左節點，T作為右節點，RGT作為根節點

6、最後剩10.15，沒有可以比較的對象，相加10+15=25，FOE作為左節點，RGT作為右節點

根節點不取值，每個左子節點取值0，右子節點取值1，將每個字母從根節點開始遍歷，沿途的取值組成編碼：

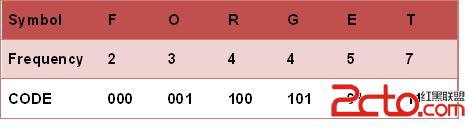
首先選擇一個文本，統計每個字符出現的次數，組成以下數組：
typedef struct FrequencyTreeNode {
int freq;
char c;
struct FrequencyTreeNode *left;
struct FrequencyTreeNode *right;
} FrequencyTreeNodeStruct, *pFrequencyTreeNodeStruct;

然後將獲得的數組frequencies進行排序，按照freq由小到大的順序組成一個二叉查找樹，FrequencyTreeNodeStruct，從二叉查找樹中找到最小的節點，從樹中刪除，再取最小的節點，兩個子節點，組成一個新的樹，根節點c為0，freq為兩個子節點的和，加入frequencies中，並排序，重復該步驟，一直到frequencies中只有一個節點，則該節點為Huffman coding tree的根節點

以short類型按照前述的規則為每個字符編碼，爾後將文本翻譯為Huffman coding，再通過Huffman coding tree進行解碼，驗證編碼的正確性。


3，代碼實現

1. #include
2. #define n 5 //葉子數目
3. #define m (2*n-1) //結點總數
4. #define maxval 10000.0
5. #define maxsize 100 //哈夫曼編碼的最大位數
6.  
7.  
8. //定義結構體
9. typedef struct FrequencyTreeNode {
10. int freq;
11. char c;
12. struct FrequencyTreeNode *left;
13. struct FrequencyTreeNode *right;
14. } FrequencyTreeNodeStruct, *pFrequencyTreeNodeStruct;
15.  
16.  
17. FrequencyTreeNodeStruct frequencies[MAXALPABETNUM];
18.  
19.  
20. typedef struct
21. {
22. char bits[n]; //位串
23. int start; //編碼在位串中的起始位置
24. char ch; //字符
25. }codetype;
26.  
27.  
28. // 讀取文件內容，統計字符以及出現頻率
29. void readTxtStatistics(char* fileName)
30. {
31. unsigned int nArray[52] = {0};
32. unsigned int i, j;
33. char szBuffer[MAXLINE];
34. int k=0;
35. // 讀取文件內容
36. FILE* fp = fopen(fileName, );
37. if (fp != NULL)
38. { /*讀取文件內容,先統計字母以及出現次數*/
39. while(fgets(szBuffer, MAXLINE, fp)!=NULL)
40. {
41. for(i = 0; i < strlen(szBuffer); i++)
42. {
43. if(szBuffer[i] <= 'Z' && szBuffer[i] >= 'A')
44. {
45. j = szBuffer[i] - 'A';
46. }
47. else if(szBuffer[i] <= 'z' && szBuffer[i] >= 'a')
48. {
49. j = szBuffer[i] - 'a' + 26;
50. }
51. else
52. continue;
53. nArray[j]++;
54. }
55. }
56.  
57.  
58. // 然後賦值給frequencies數組
59. for(i = 0, j = 'A'; i < 52; i++, j++)
60. {
61. if (nArray[i] >0)
62. {
63. /*****/
64. frequencies[k].c=j;
65. frequencies[k].freq=nArray[i];
66. frequencies[k].left=NULL;
67. frequencies[k].right=NULL;
68. k++;
69. printf(%c:%d\n, j, nArray[i]);
70. }
71. if(j == 'Z')
72. j = 'a' - 1;
73. }
74. }
75. }
76.  
77.  
78. //建立哈夫曼樹
79. void huffMan(frequencies tree[]){
80. int i,j,p1,p2;//p1,p2分別記住每次合並時權值最小和次小的兩個根結點的下標
81. float small1,small2,f;
82. char c;
83. for(i=0;i
84. {
85. tree[i].parent=0;
86. tree[i].lchild=-1;
87. tree[i].rchild=-1;
88. tree[i].weight=0.0;
89. }
90. printf(【依次讀入前%d個結點的字符及權值(中間用空格隔開)】\n,n);
91.  
92.  
93. //讀入前n個結點的字符及權值
94. for(i=0;i
95. {
96. printf(輸入第%d個字符為和權值,i+1);
97. scanf(%c %f,&c,&f);
98. getchar();
99. tree[i].ch=c;
100. tree[i].weight=f;
101. }
102. //進行n-1次合並，產生n-1個新結點
103. for(i=n;i
104. {
105. p1=0;p2=0;
106. //maxval是float類型的最大值
107. small1=maxval;small2=maxval;
108. //選出兩個權值最小的根結點
109. for(j=0;j
110. {
111. if(tree[j].parent==0)
112. if(tree[j].weight
113. {
114. small2=small1; //改變最小權、次小權及對應的位置
115. small1=tree[j].weight;
116. p2=p1;
117. p1=j;
118. }
119. else if(tree[j].weight
120. {
121. small2=tree[j].weight; //改變次小權及位置
122. p2=j;
123. }
124. tree[p1].parent=i;
125. tree[p2].parent=i;
126. tree[i].lchild=p1; //最小權根結點是新結點的左孩子
127. tree[i].rchild=p2; //次小權根結點是新結點的右孩子
128. tree[i].weight=tree[p1].weight+tree[p2].weight;
129. }
130. }
131. }
132.  
133.  
134. //根據哈夫曼樹求出哈夫曼編碼，code[]為求出的哈夫曼編碼，tree[]為已知的哈夫曼樹
135. void huffmancode(codetype code[],frequencies tree[])
136. {
137. int i,c,p;
138. codetype cd; //緩沖變量
139. for(i=0;i
140. {
141. cd.start=n;
142. cd.ch=tree[i].ch;
143. c=i; //從葉結點出發向上回溯
144. p=tree[i].parent; //tree[p]是tree[i]的雙親
145. while(p!=0)
146. {
147. cd.start--;
148. if(tree[p].lchild==c)
149. cd.bits[cd.start]='0'; //tree[i]是左子樹，生成代碼'0'
150. else
151. cd.bits[cd.start]='1'; //tree[i]是右子樹，生成代碼'1'
152. c=p;
153. p=tree[p].parent;
154. }
155. code[i]=cd; //第i+1個字符的編碼存入code[i]
156. }
157. }
158.  
159.  
160.  
161.  
162. //根據哈夫曼樹解碼
163. void decode(hufmtree tree[])
164. {
165. int i,j=0;
166. char b[maxsize];
167. char endflag='2'; //電文結束標志取2
168. i=m-1; //從根結點開始往下搜索
169. printf(輸入發送的編碼(以'2'為結束標志)：);
170. gets(b);
171. printf(編碼後的字符為);
172. while(b[j]!='2')
173. {
174. if(b[j]=='0')
175. i=tree[i].lchild; //走向左子節點
176. else
177. i=tree[i].rchild; //走向右子節點
178. if(tree[i].lchild==-1) //tree[i]是葉結點
179. {
180. printf(%c,tree[i].ch);
181. i=m-1; //回到根結點
182. }
183. j++;
184. }
185. printf(\ );
186. if(tree[i].lchild!=-1&&b[j]!='2') //文本讀完，但尚未到葉子結點
187. printf(\ ERROR\n); //輸入文本有錯
188. }
189.  
190.  
191.  
192.  
193. void main()
194. {
195. printf(---------------—— 哈夫曼編碼實戰 ——\n);
196. printf(總共有%d個字符\n,n);
197. frequencies tree[m];
198. codetype code[n];
199. int i,j;//循環變量
200. huffMan(tree);//建立哈夫曼樹
201. huffmancode(code,tree);//根據哈夫曼樹求出哈夫曼編碼
202. printf(【輸出每個字符的哈夫曼編碼】\n);
203. for(i=0;i
204. {
205. printf(%c: ,code[i].ch);
206. for(j=code[i].start;j
207. printf(%c ,code[i].bits[j]);
208. printf(\ );
209. }
210. printf(【讀入內容，並進行編碼】\n);
211. // 開始編碼
212. decode(tree);
213. }