下圖描述的是從問題引出到問題變異的思維過程:
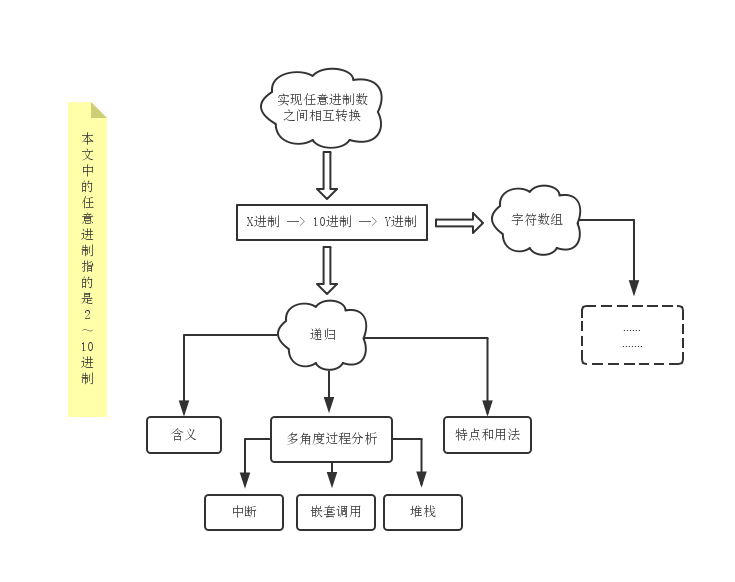
本文以數制轉換為引,對遞歸進行分析。主要是從多角度分析遞歸過程及討論遞歸特點和用法。
一次在完成某個程序時,突然想要實現任意進制數相互轉換,於是就琢磨,至少涉及以下參數:
遞歸就是遞歸函數。遞歸函數是直接或間接調用自身的函數。舉個例子:
1 /*
2 ** 接受一個整型值(無符號),把它轉換為字符並打印它,前導零被刪除。
3 */
4 #include <stdio.h>
5 void binary_to_ascii( unsigned int value ) {
6 unsigned int quotient;
7 quotient = value / 10;
8 if( quotient != 0)
9 binary_tc_ascii( quotient );
10 putchar( value % 10 + '0' );
11 }
另外遞歸還有所謂“三個條件”,“兩個階段”。我就不說了。實際應用時一般都很自然的滿足條件。
2. 遞歸過程分析中斷角度看例:有5人從左至右坐,右邊人的年齡比相鄰左邊人大2歲,最左邊的那個人10歲。問最右邊人年齡。程序2: age.c 1 #include <stdio.h>
2 age(int n) {
3 int c;
4 if( n == 1 )
5 c = 10;
6 else
7 c = age( n-1 ) + 2;
8 return(c);
9 }
10
11 int main() {
12 printf("%d\n\n",age( 5 ) );
13 return 0;
14 }
表達式: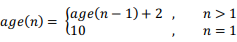
遞推和回推過程:
這跟中斷有什麼聯系呢?現在看來確實不很明顯,不過最初我就是由它想到《微機原理》中的中斷的:從age(5)開始執行,然後調用age(4),即來一個中斷,此時先保護現場,然後一直遞歸直到n=1時,中斷結束,然後層層返回,也就是不斷恢復現場的過程。
嵌套調用角度:
嵌套調用關系圖:
上面從不同角度對遞歸過程進行了分析。而際應用時並不要求你搞清楚每個遞歸的內部過程,重要的是用對。
下面主要是不恰當應用遞歸的一些例子:
許多教材中都把計算階乘和菲波那契數列用來說明遞歸,然而前者中遞歸並沒有提供任何優越之處,後者中遞歸的效率非常之低。
看一下極端的菲波那契數求解:
表達式:
程序3:fib_rec.c
1 /*
2 ** 用遞歸方法計算第n個菲波那契數列的值。
3 */
4
5 int fibonacci( int n ) {
6 if( n <= 2 )
7 return 1;
8 return fibonacci( n - 1 ) + fibonacci( n - 2 );
9 }
這裡有一個陷阱:它使用遞歸步驟計算fibonacci( n -1)和 fibonacci( n -2)。但是,在計算 fibonacci( n -1)時也將計算 fibonacci( n -2)。這個額外的代價有多大呢? 答案是:它的代價遠遠不止一個冗余計算:每個遞歸調用都會觸發另外兩個遞歸調用,面這兩個調用的任何一個還並將觸發兩個遞歸調用,再接下去的調用也是如此。這樣,冗余計算的數量增長得非常快。例如,在遞歸計算fibonacci(10)時,fibonacci(3)的值被計算了21次。但是在遞歸計算fibonacci(30)時,fibonacci(3)的值被計算了317811次,當然,這317811次產生的結果是完全一樣的,除了其中之一外,其余的純屬浪費。 想得更極端一些,假如你在程序中遞歸時不是兩次而是3次,4次,更多次的調用自身,那我想可能會讓程序崩潰吧。 現在讓我們嘗試用循環代替遞歸:程序4:fib_iter.c 1 int fibonacci( int n ) {
2 int result;
3 int previous_result;
4 int next_older_result;
5 result = previous_result = 1;
6 while(n > 2 ) {
7 n -= 1;
8 next_older_result = previous_result;
9 previous_result = result;
10 result = previous_result + next_older_result;
11 }
12 return result;
13 }
OK,說到這了,本文引子是數制轉換,總得說點數制轉換點題是吧。嗯,把題目都忘記了,回引子看一下吧。
1 #ifndef _CONERT_H
2 #define _CONERT_H
3 #include <stdio.h>
4 #include <math.h>
5 #endif
6
7 /*
8 **main()
9 */
10
11 int conert2any( int scr, int dest_d, int pow_base ) {
12 /*
13 ** 調用該函數時參數pow_base必須為0
14 */
15 int quotient, result;
16 int dest_d_base = 10;
17 quotient = scr / dest_d;
18 if( quotient != 0 )
19 result = ( scr % dest_d ) * pow( dest_d_base, pow_base) + conert2any( quotient, dest_d, ++pow_base );
20 else
21 result = ( scr % dest_d ) * pow( dest_d_base, pow_base);
22 return ( result );
23 }
OK,這個數制轉換程序用遞歸實現,沒什麼問題,但受上例啟發它也可以改為循環:
1 do {
2 result += (scr % dest_d ) * pow( dest_d_base, pow_base++ );
3 } while( scr /= dest_d != 0 )
相比於遞歸,它更短小精悍,效率也高些。
經過兩個遞歸改為循環的例子,你應該發現這兩個例子有一個共同點:遞歸調用時最後執行的語句是return 。
對於這種調用時最後執行的是return的遞歸,有一種專門的稱呼:尾部遞歸。
可以發現一般情況下尾部遞歸都可以改為相應的循環形式,而且更簡潔高效。
那什麼時候才必須用遞歸呢?據我目前的經驗和思考,只有程序1--逆序打印是必須的,其它好像沒有必須用遞歸的。
好了,到這遞歸也告一段落了,來個小插曲,談一下我寫程序5時的一些感受:
實現這個進制轉換函數時,對遞歸的理解還不深,犯了現在看來可笑的錯誤:其中要用遞歸實現加權求和,我還曾苦思如何實現累加呢,每一次調用完後變量都銷毀了,如何累加呢?苦思的結果是:利用靜態變量保存累加的值。如果到此為止的話我也不會進一步學習遞歸。因為我想,雖然這樣能實現,可是不完美,即便碧波函數調用完了,靜態變量依然在占著空間,而且再次調用前還得先清零。C語言的遞歸不該是如此麻煩的,一定是我哪裡想差了,於是我就反復看書上的例子,終於醒悟:直接用return返回不就可以實現累加了嘛。唉,當時腦子真是灌了漿糊了。
言歸正傳,全文結束,對遞歸總結一下:
說明:
date: 2014-12-10