構造哈夫曼樹的過程是這樣的
一、構成初始集合
對給定的n個權值{W1,W2,W3,...,Wi,...,Wn}構成n棵二叉樹的初始集合F={T1,T2,T3,...,Ti,...,Tn}，其中每棵二叉樹Ti中只有一個權值為Wi的根結點，它的左右子樹均為空。（為方便在計算機上實現算法，一般還要求以Ti的權值Wi的升序排列。）
二、選取左右子樹
在F中選取兩棵根結點權值最小的樹作為新構造的二叉樹的左右子樹，新二叉樹的根結點的權值為其左右子樹的根結點的權值之和。
三、刪除左右子樹
從F中刪除這兩棵樹，並把這棵新的二叉樹同樣以升序排列加入到集合F中。
四、重復二和三兩步，
重復二和三兩步，直到集合F中只有一棵二叉樹為止。
舉個例子
有個序列是(7,9,2,6,32,3,21,10)
叫你求哈夫曼樹
步驟一：把這些點都看成是一個只有根結點的樹的集合F
步驟二，選2個值最小的樹
步驟三：在這些樹的集合F中刪除這2棵樹
然後把 
構成一顆二叉樹
變成了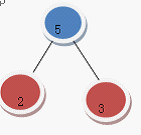
（5 = 2 + 3）
然後把這個樹加入到集合F
5代表這棵樹的權值
然後繼續上述步驟
肯定是選 5 和 6
把這2個構成二叉樹
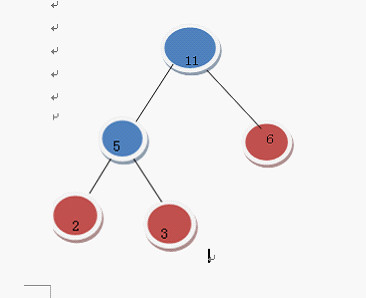
在F中刪除5 6 加入11這棵樹
變成了
繼續上述步驟
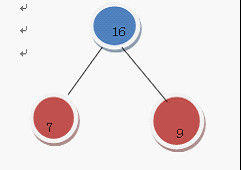
選7 和 9
在F中刪除7 和9
加入16這棵樹
變成了
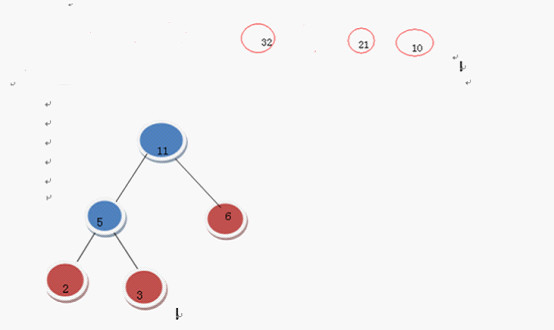
繼續上述步驟
選 10 和11
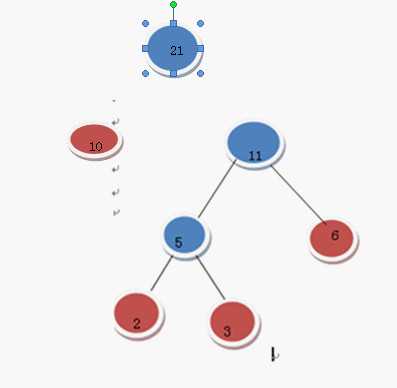
在F中刪除10 和11 加入21這棵樹
繼續上述步驟
選16和21 （有2個21，隨便選哪個）
我選那個只有一個根結點的21好了
16和21構成二叉樹
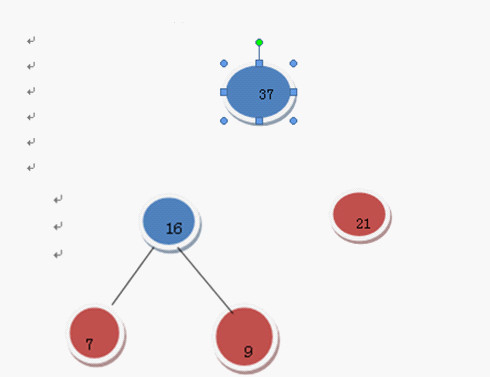
在F中刪除這16和21這兩棵樹
加入37這棵樹
繼續上述步驟
選21和32
構成二叉樹
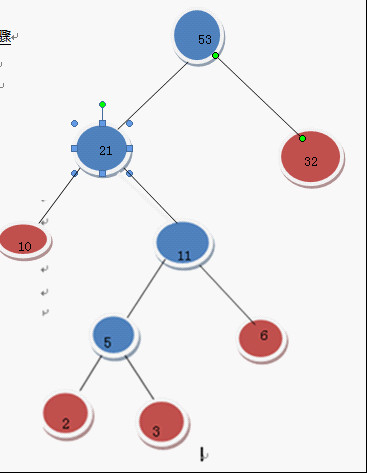
在F中刪除21和32這2兩棵樹
加入53這棵樹
還是繼續上面步驟
把F中的兩棵樹合並成一棵樹
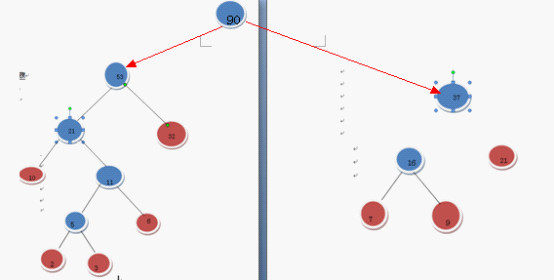
完成了!
C語言代碼實現：
/*-------------------------------------------------------------------------
* Name: 哈夫曼編碼源代碼。
* Date: 2011.04.16
* Author: Jeffrey Hill+Jezze(解碼部分)
* 在 Win-TC 下測試通過
* 實現過程：著先通過 HuffmanTree() 函數構造哈夫曼樹，然後在主函數 main()中
* 自底向上開始(也就是從數組序號為零的結點開始)向上層層判斷，若在
* 父結點左側，則置碼為 0,若在右側,則置碼為 1。最後輸出生成的編碼。
*------------------------------------------------------------------------*/
#include <stdio.h>
#include<stdlib.h>
#define MAXBIT 100
#define MAXVALUE 10000
#define MAXLEAF 30
#define MAXNODE MAXLEAF*2 -1
typedef struct
{
int bit[MAXBIT];
int start;
} HCodeType; /* 編碼結構體 */
typedef struct
{
int weight;
int parent;
int lchild;
int rchild;
int value;
} HNodeType; /* 結點結構體 */
/* 構造一顆哈夫曼樹 */
void HuffmanTree (HNodeType HuffNode[MAXNODE], int n)
{
/* i、j： 循環變量，m1、m2：構造哈夫曼樹不同過程中兩個最小權值結點的權值，
x1、x2：構造哈夫曼樹不同過程中兩個最小權值結點在數組中的序號。*/
int i, j, m1, m2, x1, x2;
/* 初始化存放哈夫曼樹數組 HuffNode[] 中的結點 */
for (i=0; i<2*n-1; i++)
{
HuffNode[i].weight = 0;//權值
HuffNode[i].parent =-1;
HuffNode[i].lchild =-1;
HuffNode[i].rchild =-1;
HuffNode[i].value=i; //實際值，可根據情況替換為字母
} /* end for */
/* 輸入 n 個葉子結點的權值 */
for (i=0; i<n; i++)
{
printf ("Please input weight of leaf node %d: \n", i);
scanf ("%d", &HuffNode[i].weight);
} /* end for */
/* 循環構造 Huffman 樹 */
for (i=0; i<n-1; i++)
{
m1=m2=MAXVALUE; /* m1、m2中存放兩個無父結點且結點權值最小的兩個結點 */
x1=x2=0;
/* 找出所有結點中權值最小、無父結點的兩個結點，並合並之為一顆二叉樹 */
for (j=0; j<n+i; j++)
{
if (HuffNode[j].weight < m1 && HuffNode[j].parent==-1)
{
m2=m1;
x2=x1;
m1=HuffNode[j].weight;
x1=j;
}
else if (HuffNode[j].weight < m2 && HuffNode[j].parent==-1)
{
m2=HuffNode[j].weight;
x2=j;
}
} /* end for */
/* 設置找到的兩個子結點 x1、x2 的父結點信息 */
HuffNode[x1].parent = n+i;
HuffNode[x2].parent = n+i;
HuffNode[n+i].weight = HuffNode[x1].weight + HuffNode[x2].weight;
HuffNode[n+i].lchild = x1;
HuffNode[n+i].rchild = x2;
printf ("x1.weight and x2.weight in round %d: %d, %d\n", i+1, HuffNode[x1].weight, HuffNode[x2].weight); /* 用於測試 */
printf ("\n");
} /* end for */
/* for(i=0;i<n+2;i++)
{
printf(" Parents:%d,lchild:%d,rchild:%d,value:%d,weight:%d\n",HuffNode[i].parent,HuffNode[i].lchild,HuffNode[i].rchild,HuffNode[i].value,HuffNode[i].weight);
}*///測試
} /* end HuffmanTree */
//解碼
void decodeing(char string[],HNodeType Buf[],int Num)
{
int i,tmp=0,code[1024];
int m=2*Num-1;
char *nump;
char num[1024];
for(i=0;i<strlen(string);i++)
{
if(string[i]=='0')
num[i]=0;
else
num[i]=1;
}
i=0;
nump=&num[0];
while(nump<(&num[strlen(string)]))
{tmp=m-1;
while((Buf[tmp].lchild!=-1)&&(Buf[tmp].rchild!=-1))
{
if(*nump==0)
{
tmp=Buf[tmp].lchild ;
}
else tmp=Buf[tmp].rchild;
nump++;
}
printf("%d",Buf[tmp].value);
}
}
int main(void)
{
HNodeType HuffNode[MAXNODE]; /* 定義一個結點結構體數組 */
HCodeType HuffCode[MAXLEAF], cd; /* 定義一個編碼結構體數組， 同時定義一個臨時變量來存放求解編碼時的信息 */
int i, j, c, p, n;
char pp[100];
printf ("Please input n:\n");
scanf ("%d", &n);
HuffmanTree (HuffNode, n);
for (i=0; i < n; i++)
{
cd.start = n-1;
c = i;
p = HuffNode[c].parent;
while (p != -1) /* 父結點存在 */
{
if (HuffNode[p].lchild == c)
cd.bit[cd.start] = 0;
else
cd.bit[cd.start] = 1;
cd.start--; /* 求編碼的低一位 */
c=p;
p=HuffNode[c].parent; /* 設置下一循環條件 */
} /* end while */
/* 保存求出的每個葉結點的哈夫曼編碼和編碼的起始位 */
for (j=cd.start+1; j<n; j++)
{ HuffCode[i].bit[j] = cd.bit[j];}
HuffCode[i].start = cd.start;
} /* end for */
/* 輸出已保存好的所有存在編碼的哈夫曼編碼 */
for (i=0; i<n; i++)
{
printf ("%d 's Huffman code is: ", i);
for (j=HuffCode[i].start+1; j < n; j++)
{
printf ("%d", HuffCode[i].bit[j]);
}
printf(" start:%d",HuffCode[i].start);
printf ("\n");
}
/* for(i=0;i<n;i++){
for(j=0;j<n;j++)
{
printf ("%d", HuffCode[i].bit[j]);
}
printf("\n");
}*/
printf("Decoding?Please Enter code:\n");
scanf("%s",&pp);
decodeing(pp,HuffNode,n);
getch();
return 0;
}
哈夫曼樹 在一般的數據結構的書中，樹的那章後面，著者一般都會介紹一下哈夫曼(HUFFMAN)樹和哈夫曼編碼。哈夫曼編碼是哈夫曼樹的一個應用。哈夫曼編碼應用廣泛，如JPEG中就應用了哈夫曼編碼。
首先介紹什麼是哈夫曼樹。哈夫曼樹又稱最優二叉樹，是一種帶權路徑長度最短的二叉樹。所謂樹的帶權路徑長度，就是樹中所有的葉結點的權值乘上其到根結點的路徑長度（若根結點為0層，葉結點到根結點的路徑長度為葉結點的層數）。樹的帶權路徑長度記為WPL=(W1*L1+W2*L2+W3*L3+...+Wn*Ln)，N個權值Wi(i=1,2,...n)構成一棵有N個葉結點的二叉樹，相應的葉結點的路徑長度為Li(i=1,2,...n)。可以證明哈夫曼樹的WPL是最小的。
哈夫曼在上世紀五十年代初就提出這種編碼時，根據字符出現的概率來構造平均長度最短的編碼。它是一種變長的編碼。在編碼中，若各碼字長度嚴格按照碼字所對應符號出現概率的大小的逆序排列，則編碼的平均長度是最小的。（注：碼字即為符號經哈夫曼編碼後得到的編碼，其長度是因符號出現的概率而不同，所以說哈夫曼編碼是變長的編碼。）
然而怎樣構造一棵哈夫曼樹呢？最具有一般規律的構造方法就是哈夫曼算法。一般的數據結構的書中都可以找到其描述：
一、對給定的n個權值{W1,W2,W3,...,Wi,...,Wn}構成n棵二叉樹的初始集合F={T1,T2,T3,...,Ti,...,Tn}，其中每棵二叉樹Ti中只有一個權值為Wi的根結點，它的左右子樹均為空。（為方便在計算機上實現算法，一般還要求以Ti的權值Wi的升序排列。）
二、在F中選取兩棵根結點權值最小的樹作為新構造的二叉樹的左右子樹，新二叉樹的根結點的權值為其左右子樹的根結點的權值之和。
三、從F中刪除這兩棵樹，並把這棵新的二叉樹同樣以升序排列加入到集合F中。
四、重復二和三兩步，直到集合F中只有一棵二叉樹為止。
用C語言實現上述算法，可用靜態的二叉樹或動態的二叉樹。若用動態的二叉樹可用以下數據結構： struct tree{
float weight; /*權值*/
union{
char leaf; /*葉結點信息字符*/
struct tree *left; /*樹的左結點*/
};
struct tree *right; /*樹的右結點*/
};
struct forest{ /*F集合，以鏈表形式表示*/
struct tree *ti; /* F中的樹*/
struct forest *next; /* 下一個結點*/
};
例：若字母A，B，Z，C出現的概率為：0.75,0.54,0.28,0.43；則相應的權值為：75，54，28，43。
構造好哈夫曼樹後，就可根據哈夫曼樹進行編碼。例如：上面的字符根據其出現的概率作為權值構造一棵哈夫曼樹後，經哈夫曼編碼得到的對應的碼值。只要使用同一棵哈夫曼樹，就可把編碼還原成原來那組字符。顯然哈夫曼編碼是前綴編碼，即任一個字符的編碼都不是另一個字符的編碼的前綴，否則，編碼就不能進行翻譯。例如：a,b,c,d的編碼為：0，10，101，11，對於編碼串：1010就可翻譯為bb或ca，因為b的編碼是c的編碼的前綴。剛才進行哈夫曼編碼的規則是從根結點到葉結點（包含原信息）的路徑，向左孩子前進編碼為0，向右孩子前進編碼為1，當然你也可以反過來......余下全文>>
哈夫曼樹:
給定n個權值作為n個葉子結點，構造一棵二叉樹，若帶權路徑長度達到最小，稱這樣的二叉樹為最優二叉樹，也稱為哈夫曼樹(Huffman tree)。哈夫曼樹是帶權路徑長度最短的樹，權值較大的結點離根較近。
哈夫曼樹的構造：
假設給定的權值如下：3,5,7,8,10,15；
首先取集合中最小的兩個數：3+5=8，再刪除集合中3和5的值，把8放入原集合,
原集合變成:7,8,8,10,15；
8
/ \
3 5
再從7,8,8,10,15中再取2個最小的數構成一個樹
15
/ \
8 7
/ \
3 5
再從8,10,15,15中再取2個最小的數構成一個樹:
18
/ \
8 10
再從15,15,18中取兩個最小數:15,15,構成樹:
30
/ \
15 15
/ \
8 7
/ \
3 5
最後把18,30構成樹(此時集合中已經沒元素了，就形成了哈夫曼樹):
48
/ \
30 18
/ \ / \
15 15 8 10
/ \
8 7
/ \
3 5
希望你能看懂！！
