前言:在網上看到不少解一元二次方程的小程序,在使用時總得出一大堆小數,感覺很不爽,遂自己重新寫了一遍。
首先,先回憶一下一元二次方程的求根公式:
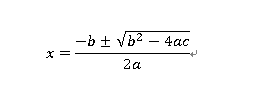


此時同時輸出delta的值,小於0,無解。
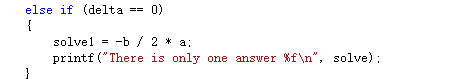
當delta等於0,只有一個實數根,沒什麼好講。
現在涉及一個問題就是如何判斷整數

此處為了避免互相干擾,用了兩個變量,sqr用於判斷是否為整數,如果是整數,則用sqr1計算
如何判斷是否為整數呢?這裡可以利用int形和double形的性質。采用判斷(int)sqr和 (int)(sqr + 0.9999999)的大小來判斷sqr是不是整數。[double形一般精確到小數點後6 位,所以這裡用了7個9]。然後強制轉換成int型,如果為整數,(int)(sqr + 0.9999999)不會進位,x=y。不是整數,反之。
然後如果為整數,先計算sqrt(delta)後代入計算。
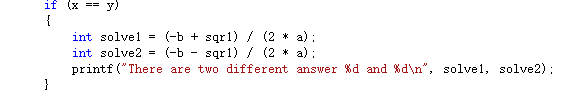
(2)sqrt(delta)不是整數時
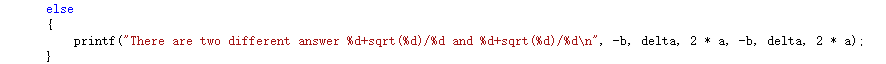
對,保留根號!
後記:寫這一段小程序最初是為繁多的坑爹的解方程數學題所惱,想快點完成作業~~於是在那個月黑風高的晚上寫完作業後順便把這篇文章寫了。
#include <stdio.h>
#include <math.h>
int main(void)
{
int a, b, c; //定義一元二次方程的三個數值;
printf("請依次輸入一元二次方程的三個參數a b c,中間以空格隔開\n");
scanf("%d %d %d", &a, &b, &c); //依次輸入一元二次方程的三個參數
double delta = b*b - 4*a*c; //定義delta的值為b*b - 4*a*c
double x1 = (-b + sqrt(delta))/(2 * a);
double x2 = (-b - sqrt(delta))/(2 * a);
if (delta>0) //delta大於0時,方程有兩個解
{
printf("一元二次方程有兩個解\n");
printf("一元二次方程的第一個解,x1 = %f\n",x1);
printf("一元二次方程的第二個解,x2 = %f\n",x2);
}
else if (delta ==0) //delta等於0,方程有兩個相同的解
{
printf("一元二次方程有兩個相同的解\n");
printf("一元二次方程的解為x1 = x2 =%f\n",x1);
}
else //delta小於0時,方程沒有解
{
printf("一元二次方程沒有解\n");
}
return 0;
}
#include <stdio.h>
#include <math.h>
void main ()
{
double sqrt(double x);
int a,b,c;
double x1,x2,x,e,d,g,f;
scanf("%d %d %d",&a,&b,&c);
d=b*b-4*a*c;
if (a==0)
{ if (b!=0)
{x=-(double)c/(double)b;
if (x==0)
{x=-x;
printf("x=%.6lf\n",x);}
else
printf("x=%.6lf\n",x);
}
else
printf("Input error!\n");}
else if (d<0)
{d=-d;
e=sqrt(d);
g=-(double)b/(2*(double)a);
f=e/(2*a);
if (g!=0)
printf("x1=%.6lf+%.6lfi\nx2=%.6lf-%.6lfi\n",g,f,g,f);
else
printf("x1=%.6lfi\nx2=-%.6lfi\n",f,f);}
else if (d==0)
{ x1=x2=-b/(2*a);
printf("x1=x2=%.6lf\n",x1);}
else
{ e=sqrt(d);
x1=(-b+e)/(2*a);
x2=(-b-e)/(2*a);
printf("x1=%.6lf\nx2=%.6lf\n",x1,x2);}
}
這個可以,但也許不夠簡便