程式師世界 >> 編程語言 >> C語言 >> 關於C語言 >> 數據結構（C實現）------- 遍歷二叉樹

數據結構（C實現）------- 遍歷二叉樹

編輯：關於C語言

數據結構（C實現）------- 遍歷二叉樹

本文是自己學習所做筆記，歡迎轉載，但請注明出處：http://blog.csdn.net/jesson20121020

二叉樹是另一中樹型結構，它的特點是每個結點至多只有兩棵子樹（即二叉樹中不存在度大於２的結點），並且，二叉樹的子樹有左右之分，其次序不能任意顛倒。

根據二叉樹的的遞歸定義可知，二叉樹是由3個基本單元組成，根結點、左子樹和右子樹，因此，若能依次遍歷這三部分，便是遍歷了整個二叉樹。假如以L、D、R分別表示遍歷左子樹、訪問根結點和遍歷右子樹，則可能有DLR、LDR、LRD、DRL、RDL、RLD這6種遍歷二叉樹的方案。若限定先左後右，則只有前3種情況，分別稱為先序遍歷、中序遍歷和後序遍歷，另外，還有一種遍歷方法，即從上到下，從左到右依次遍歷二叉樹的每個結點，稱之為層次遍歷。故，共有4種遍歷二叉樹的方法。

二叉樹遍歷操作定義：

1. 先序遍歷二叉樹的操作定義：

若二叉樹為空，則空操作；否則

1）訪問根結點

2）先序遍歷左子樹

3）先序遍歷右子樹

2. 中序遍歷二叉樹的操作定義：

若二叉樹為空，則空操作；否則

1）中序遍歷左子樹

2）訪問根結點

3）中序遍歷右子樹

3. 後序遍歷二叉樹的操作定義：

若二叉樹為空，則空操作；否則

1）後序遍歷左子樹

2）後序遍歷右子樹

3）訪問根結點

4. 層次遍歷二叉樹的操作定義：

若二叉樹為空，則空操作；否則

1）從上到下

2）同一層，從左到右依次遍歷

二叉樹的存儲結構：

1. 順序存儲結構：

#define MAX_TREE_SIZE 100
typedef char TElemType; 
typedef TElemType SqBiTree[MAX_TREE_SIZE];
SqBiTree bt;

2. 鏈式存儲結構：

//二叉樹的的
#define MAXSIZE 100 //二叉樹中最多的結點數　
typedef char TElemType; 
typedef struct BiTNode{
	TElemType data;
	struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

二叉樹的遍歷具體實現：

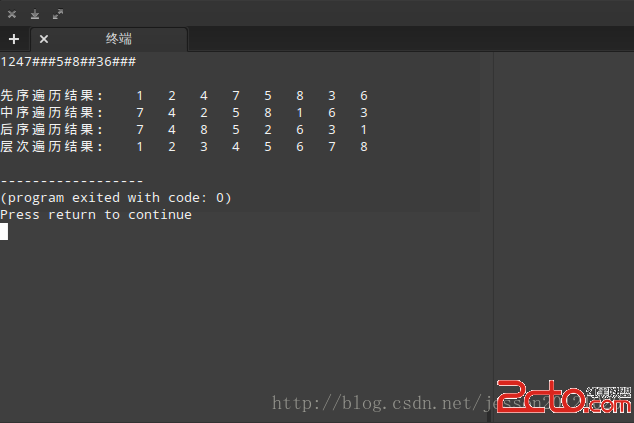
#include 
#include 

//二叉樹的的
#define MAXSIZE 100 //二叉樹中最多的結點數　
typedef char TElemType; 
typedef struct BiTNode{
	TElemType data;
	struct BiTNode *lchild,*rchild;
}BiTNode,*BiTree;

//定義函數指針
typedef void(* Visit)(BiTree);

//二叉樹的初始化
void Init_BiTree(BiTree *T){
	*T = NULL;
}

//判斷二叉樹是否為空,返回1
int IsEmpty_BiTree(BiTree *T){
	return *T == NULL;
}

//創建二叉樹
void Create_BiTree(BiTree *T){
	char ch;
	ch = getchar();
	//當輸入的是"#"時，認為該子樹為空
	if(ch == '#')
		*T = NULL;
	//創建樹結點
	else{
		*T = (BiTree)malloc(sizeof(BiTNode));
		(*T)->data = ch; //生成樹結點
		//生成左子樹
		Create_BiTree(&(*T)->lchild);
		//生成右子樹
		Create_BiTree(&(*T)->rchild);
	}
}

//輸出結點的值
void Print_BiTreeNode(BiTree T){
	printf("%c\t",T->data);
	
}

//先序遍歷二叉樹
void PreOrder_BiTree(BiTree T,Visit visit){
	if(!IsEmpty_BiTree(&T)){
		visit(T);
		PreOrder_BiTree(T->lchild,visit);
		PreOrder_BiTree(T->rchild,visit);
	}
}
//中序遍歷二叉樹
void InOrder_BiTree(BiTree T,Visit visit){
	if(!IsEmpty_BiTree(&T)){
		InOrder_BiTree(T->lchild,visit);
		visit(T);
		InOrder_BiTree(T->rchild,visit);
	}
}

//後序遍歷二叉樹　
void PostOrder_BiTree(BiTree T,Visit visit){
	if(!IsEmpty_BiTree(&T)){
		PostOrder_BiTree(T->lchild,visit);
		PostOrder_BiTree(T->rchild,visit);
		visit(T);
	}
}

//層次遍歷二叉樹　
void LevelOrder_BiTree(BiTree T,Visit visit){
	//用一個隊列保存結點信息,這裡的隊列采用的是順序隊列中的數組實現
	int front = 0;
	int rear = 0;
	BiTree BiQueue[MAXSIZE];
	BiTree tempNode;
	if(!IsEmpty_BiTree(&T)){
		//將根結點加入到隊列中　
		BiQueue[rear++] = T;
		
		while(front != rear){
			//取出隊頭元素，並使隊頭指針向後移動一位　
			tempNode = BiQueue[front++];
			//判斷左右子樹是否為空,若為空，則加入隊列　
			if(!IsEmpty_BiTree(&(tempNode->lchild)))
				BiQueue[rear++] = tempNode->lchild;
			
			if(!IsEmpty_BiTree(&(tempNode->rchild)))
				BiQueue[rear++] = tempNode->rchild;
			
			//輸出隊頭結點元素　
			//Vist_BiTreeNode(tempNode->data);
			visit(tempNode);
		}
	}
}

int main(){
	BiTree T;
	//將二叉樹初始為一個空的二叉樹
	Init_BiTree(&T);
	//創建二叉樹
	Create_BiTree(&T);
	//先序遍歷
	printf("\n先序遍歷結果：");
	PreOrder_BiTree(T,Print_BiTreeNode);
	//中序遍歷二叉樹
	printf("\n中序遍歷結果：");
	InOrder_BiTree(T,Print_BiTreeNode);
	//後序遍歷二叉樹　
	printf("\n後序遍歷結果：");
	PostOrder_BiTree(T,Print_BiTreeNode);
	//層次遍歷二叉樹　
	printf("\n層次遍歷結果：");
	LevelOrder_BiTree(T,Print_BiTreeNode);
	return 0;
}