自然數(Natural Number)：自然數就是正整數集合，用{1, 2, 3, ...}表示，也可以是非負整數集合，用{0, 1, 2, 3, ...}表示，前都主要用於數論，後者則主要用於數理邏輯、集合論、計算機科學等。
素數(): 素數一個大於1的自然數，該自然數只有1和它本身兩個除數（自然數）。
這概念雖然簡單，但如果不知道的話程序寫將無從下手，這無異於“James, 給我寫個滿足要求的程序", 但並沒有說寫什麼樣的程序。
典型算法
最簡單最直接的方法應該就是用2到（n-1)的自然數去除n，其中n即為將要確實是數，如果每個數都不能整除，則說明n是素數。
而事實上沒有必要用2到(n-1)之間的每一個數去除n。例如要確實7是不是系數，用除到3的時候就已經可以確實7是系數而不必繼續了，即只要用2，3去除n就可以了。一般地，只要用2到n/2的自然數去除n就可以了。這樣比前面的方法要快一點。
人們還想到了一個更好一點方法：用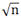
來取代n/2。
今天同學考試的問題是：給定兩個整數m,k，找出大於m同時也最靠近m的k個素數，用C語言實現如下，完整代碼參見[7、程序實現]：
void findPrimeNum(int m, int k , int xx[]) {
int i = 0, j, x = m + 1, isPrime;
while (i < k) {
isPrime = TRUE;
for ( j = 2; j <= sqrt(x); j++) { // j <= 2 也行
if ( x % j == 0 ) {
isPrime = FALSE;
break;
}
}
if (isPrime) xx[i++] = x;
x++;
}
}
更有效的算法
如果給定一個很大的自然數要確定其是否為素數，典型算法可能要費很多的時間才能確定下來。這裡有一個更好一點的算法：
boolean isPrime(int num) {
int divisor = 3;
int testLimit = num;
if (num % 2 == 0) return FALSE;
while ( testLimit > divisor ) {
if ( num % divisor == 0 ) {
return FALSE;
}
testLimit = num / divisor;
divisor += 2;
}
return TRUE;
}
參考資源
[1]Prime number, wikipedia, http://en.wikipedia.org/wiki/Prime_number
[2]Determine if an Integer is a prime number, Toby Herring, http://www.freevbcode.com/ShowCode.asp?ID=1059
清單1：C實現
/*
* 典型算法
*/
#include <stdio.h>
#include <math.h>
#define MAX_LEN 100
#define TRUE 1
#define FALSE 0
typedef int boolean;
void findPrimeNum(int m, int k , int xx[]);
void findPrimeNum2(int m, int k , int xx[]);
int isPrime(int num);
int main(void) {
int m, k, i, xx[MAX_LEN], xx2[MAX_LEN];
printf("輸入m: ");
scanf("%d", &m);
do {
printf("輸入k (k < %d): ", MAX_LEN);
scanf("%d", &k);
} while (k > MAX_LEN);
puts("運行及結果:");
findPrimeNum (m , k , xx);
findPrimeNum2 (m , k , xx2);
for (i = 0; i < k ; i++) {
printf("%d, ", xx[i]);
}
printf("\n");
for (i = 0; i < k ; i++) {
printf("%d, ", xx2[i]);
}
printf("\n");
puts("結束");
return 0;
}
void findPrimeNum(int m, int k , int xx[]) {
int i = 0, j, x = m + 1, isPrime;
while (i < k) {
isPrime = TRUE;
for ( j = 2; j <= sqrt(x); j++) { // j <= 2 也行
if ( x % j == 0 ) {
isPrime = FALSE;
break;
}
}
if (isPrime) xx[i++] = x;
x++;
}
}
void findPrimeNum2(int m, int k , int xx[]) {
int i = 0, j, x = m + 1;
while ( i < k) {
if (isPrime(x)) xx[i++] = x;
x++;
}
}
boolean isPrime(int num) {
int divisor = 3;
int testLimit = num;
if (num % 2 == 0) return FALSE;
while ( testLimit > divisor ) {
if ( num % divisor == 0 ) {
return FALSE;
}
testLimit = num / divisor;
divisor += 2;
}
return TRUE;
}
清單2：VB實現
Module Module1
Sub Main()
Dim num As Long
num = 14
If (IsPrime(num)) Then
MsgBox(num & " is Prime")
Else
MsgBox(num & " is NOT Prime")
End If
End Sub
Public Function IsPrime(ByVal TestPrime As Long) As Boolean
Dim TestNum As Long
Dim TestLimit As Long
' Eliminate even numbers
If TestPrime Mod 2 = 0 Then Exit Function
' Loop through ODD numbers starting with 3
TestNum = 3
TestLimit = TestPrime
Do While TestLimit > TestNum
If TestPrime Mod TestNum = 0 Then
' Uncomment this if you really want to know
'MsgBox("Divisible by " & TestNum)
Exit Function
End If
' There's logic to this. Think about it.
TestLimit = TestPrime \ TestNum
' Remember, we only bother to check odd numbers
TestNum = TestNum + 2
Loop
' If we made it through the loop, the number is a prime.
IsPrime = True
End Function
End Module
