斐波那契數列:
又稱黃金分割數列,指的是這樣一個數列:0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...
在數學上,斐波納契數列以如下被以遞歸的方法定義:F0=0,F1=1,Fn=F(n-1)+F(n-2)(n>=2,n∈N*),
即這個數列從第二項開始,每一項都等於前兩項之和。
特別指出:0是第0項,不是第1項。
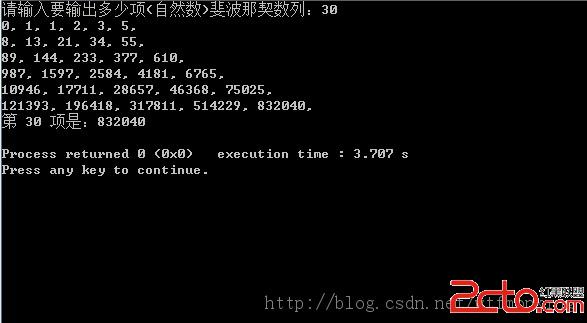
用遞歸法求斐波那契數列並列出所有項:
#includeint fun(int n) //n代表第幾項。特別指出:0是第0項,不是第1項。 { if (n <= 1) return n; else return fun(n-1) + fun(n-2); } int main() { int n; printf("請輸入要輸出多少項(自然數)斐波那契數列:"); scanf("%d",&n); //int *a = (int *)malloc((n+1)*sizeof(int));//如需存儲,使用動態內存分配n+1個空間進行存儲 int i; for (i = 0; i < n+1; i++) //輸出所有項 { printf("%d, ", fun(i)); if (i != 0 && i%5 == 0) //每五項進行一次換行(第一行多一個第0項) printf("\n"); } printf("第 %d 項是:%d\n", n, fun(n)); //輸出要求的項 return 0; }