先放一個基於背包問題原型的問題:
有兩艘貨船需要裝運N個貨箱,第一艘貨船的載重量是C1,第二艘為C2,Wi為貨箱i的重量,且W1+W2+W3+...Wn<=C1+C2,希望確定是否有一種可將所有N個貨箱全部裝船的方法,如果有,找出該方法 。
分析:
作為背包問題,通常采用的方法有窮舉(需要知道貨箱的個數),動態規劃,分支界限搜索算法,本章討論結合子集樹特征的一種窮舉算法
題目要求W1+W2+W3+...Wn<=C1+C2,即要求在總貨重不超過C1+C2這一前提下,盡可能的把貨船C1裝滿,於是問題可以轉變為:確保W1+W2+W3+...Wn<=C1+C2前提下,有多少種選擇裝船的方法使得C1裝滿。
子集樹的特征:在於對於一個節點的兩路分支只有選擇與不選擇的情況,通常選擇左分支為選擇,計數為1,反之選擇右分支為不選,計數為0;當把所有節點按照上述規則形成一顆二叉樹時,通過對樹的每次根到葉子節點的遍歷,便可得到當前選擇的選擇情況。
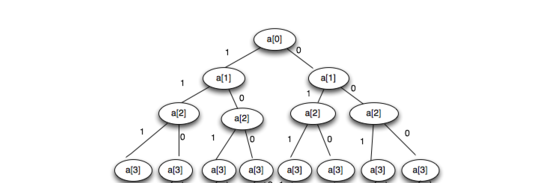
圖1 二叉子集樹
回到問題,該問題如果采用分支界限搜索算法,意味著會間接的構造一顆二叉子集樹,並預先通過條件判斷來去除部分不可能選擇,如果采用常規窮舉,在已知個數N的情況下,會產生N重的循環來逐一求解
對於圖1,如果把所有的情況按照選擇或者不選擇,把相對應的選擇號記錄下來,則會有這一結果:
000,001,010,011,100,101,110,111
轉換為對應的十進制數則為:
0,1,2,3,4,5,6,7
結合上面的結果,不難發現,如果有N個點進行構建二叉子集樹,便會有2∧N種選擇情況,所需要的結果也在[0,2∧N-1]這一范圍中獲取
改進常規窮舉算法:
通過分析可以知道,問題的所需結果在[0,2∧N-1]這一范圍中獲取,那麼可以設計出算法的框架原型
count=2<<num-1;//count為所有選擇的總計,num為貨箱的個數
while(count>=0)
{
j=count;
for(i=num;i>0;i--)//N個貨物只用比較2∧N-1次,每次移位只需向右移動N個
{
k+=(j&0x01)*(*b);//將當前選擇的數的二進制最後一位取出,並與數組中當前貨物相乘
if(k==c1)//當前重量達到第一艘貨船的重量
{
print(輸出結果);
break;
}
else if(k>c1)//當前重量超過第一艘貨船的重量
{
k-=*b;//去除當前的這次重量
break;
}
else//當前重量未達到第一艘貨船的重量
{
j>>=1;//當前數值右移一位
b++;//指向數組指針移向下一個元素的地址
continue;
}
}
if(k<c1&&(weight-k)<=c2)//當前選擇使得第一艘貨船沒有裝滿
{
print(輸出結果);
}
count--;當前選擇數減1
}
算法分析:
相比於常規的窮舉算法,該算法的用到了二重循環,外層循環為選擇數的總數,內層為每一個選擇數移位運算的次數(N個貨箱只需向右移位N位)
時間復雜度取決於貨箱N的個數,即時間仍復雜度為O(2∧N)*N,當N的個數趨近於無窮大時,算法仍然不能解決(取決於計算機能表示的二進制的位數)
附錄:完整C代碼(WIN 8.1 64位 已在VC6.0下通過)
#include<stdio.h><stdlib.h><time.h> n 4 search( *,,, main(,&,&(i=;i<n;i++,i+,& search( *a, c1, c2, count,i,j,k,flag,weight,*=,weight==(i=,b=( *)a,count=;i<num;i++,b+++=*(weight>c1+=(flag!==<<num-(count>====( *(i=n;i>;i--+=(j&)*(*(k==,weight- (k>-=*>>=++(k<c1&&(weight-k)<=,weight---=,()(end-start)/