摘要:KMP算法是字符串匹配的經典算法,由於其O(m+n)的時間復雜度,至今仍被廣泛應用。大道至簡,KMP算法非常簡潔,然而,其內部卻蘊含著玄妙的理論,以至許多人知其然而不知其所以然。本文旨在解開KMP算法的內部玄妙所在,希望能夠有助於學習與理解。
1、KMP算法
一種改進的字符串匹配算法,由D.E.Knuth與V.R.Pratt和J.H.Morris同時發現,因此稱之為KMP算法。此算法可以在O(n+m)的時間數量級上完成串的模式匹配操作,其基本思想是:每當匹配過程中出現字符串比較不等時,不需回溯指針,而是利用已經得到的“部分匹配”結果將模式向右“滑動”盡可能遠的一段距離,繼續進行比較。
2、基於有限自動機理解算法
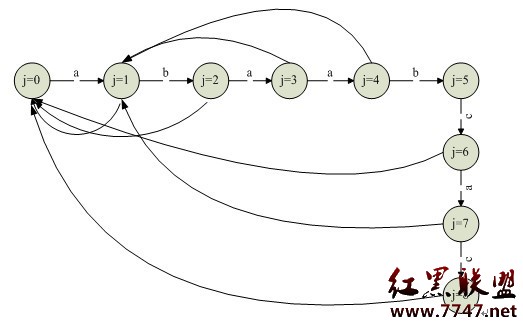
KMP 算法看似簡單,其實要完全理解還是有困難的。KMP算法其實可以看成是一個有限自動機,分為 2 部分:第一部分自動機的構造 ( 對應一般的說法就是失效函數,轉移函數, overlap 函數 ) ,第二部分在自動機上搜索過程。舉個例子: 目標串 T = acabaabaabcacaabc; 模式串 P=abaabcac ;根據模式串構造自動機,向前的箭頭表示搜索前進的方向。向後的箭頭表示不匹配的回溯,即失效函數,或者狀態變遷函數。例如:
f(j=1) = 0;
f(j=2) = 0;
f(j=3) = 1;
f(j=4) = 1;
f(j=5) = 2;
f(j=6) = 0;
f(j=7) = 1;
KMP本質上是構造了DFA並進行了模擬,因此很顯然一旦從模版T構造了自動機D,用D去匹配主串S的過程就是線性的。KMP最引人入勝的地方就在於構造D的自匹配過程,它充分利用了D是一個DAG的性質,使得構造過程也是線性的。KMP算法不需要計算變遷函數,只用到輔助數組Next,即模式串自身的特征向量。特征向量可以用模式與其自身進行比較,預先計算出來,它可用於加快字符串匹配算法與有限自動機匹配器的執行速度。
3、Next特征數組構造
模式串P開頭的任意個字符,把它稱為前綴子串,如p0p1p2…pm-1。在P的第i位置的左邊,取出k個字符,稱為i位置的左子串,即pi-k+1... pi-2 pi-1 pi。求出最長的(最大的k)使得前綴子串與左子串相匹配稱為,在第i位的最長前綴串。第i位的最長前綴串的長度k就是模板串P在位置i上的特征數n[i]特征數組成的向量稱為該模式串的特征向量。
可以證明對於任意的模式串p=p0p1…pm-1,確實存在一個由模式串本身唯一確定的與目標串無關的數組next,計算方法為:
(1) 求p0…pi-1中最大相同的前綴和後綴的長度k;
(2) next[i] = k;
作為特殊情況,當i=0時,令next[i] = -1;顯然,對於任意i(0≤i<m),有next[i] < i;假定已經計算得到next[i], 那麼next[i+1] = ? 特征數ni ( -1≤ ni ≤ i )是遞歸定義的,定義如下:
(1) n[0] = -1,對於i > 0的n[i] ,假定已知前一位置的特征數 n[i-1]= k ;
(2) 如果pi = pk ,則n[i] = k+1 ;
(3) 當pi ≠ pk 且k≠0時,則令k = n [k -1] ; 讓(3)循環直到條件不滿足;
(4) 當qi ≠ qk 且k = 0時,則ni = 0;
根據以上分析,可以得到Next特征數組的計算方法,算法代碼如下:
1.void get_next(SString T, int &next[])
2.{
3. //求模式串T的next函數值並存入數組next
4. i = 1; next[1] = 0; j = 0;
5. while (i < T[0])
6. {
7. if(j ==0 || T[i] == T[j])
8. {
9. ++i; ++j; next[i] = j;
10. }
11. else
12. {
13. j = next[j];
14. }
15. }
16.}
文獻[5]中解釋了以上計算方法存在一定缺陷,存在多比較的情況,可對其進行修正,得到如下算法:
1.void get_next(SString T, int &next[])
2.{
3. //求模式串T的next函數值並存入數組next
4. i = 1; next[1] = 0; j = 0;
5. while (i < T[0])
6. {
7. if(j ==0 || T[i] == T[j])
8. {
9. ++i; ++j;
10. if (T[i] != T[j])
11. next[i] = j;
12. else
13. next[i] = next[j];
14. }
15. else
16. {
17. j = next[j];
18. }
19. }
20.}
4、算法實現
KMP算法的難點就是有限自動機的構造和特征向量的計算。解決了這兩個問題後,具體匹配算法就很簡單了。
int Index_KMP(SString S,SString T,int pos){
//利用模式串T的next函數求T在主串S中第pos個字符之後的位置的KMP算法。
//其中,T非空,1≤pos≤StrLength(S)。
i=pos; j=1;
while(i <= S[0] && j<= T[0]){
if(j == 0 || S[i] == T[j]) { ++i; ++j; }//繼續比較後繼字符
else j = next[j];//模式串象右移動
}
if(j>T[0]) return i-T[0];//匹配成功
else return 0;
}//Index_KMP
算法相關理論分析與證明,以及算法復雜性分析,若感興趣請參考文獻[3]、[4]、[5],這裡不再贅述。
5、參考文獻
[1] http://wansishuang.javaeye.com/blog/402018
[2] http://richardxx.yo2.cn/articles/kmp和extend-kmp算法.html
[3] KMP算法講義PPT(Hu Junfeng, Peking University)
[4] 算法導論(第32章 字符串匹配)
[5] 數據結構(第4章 串)