本文主要參考:算法導論第二版
本文主要代碼:參考算法導論。
本文圖片來源:個人手工畫成、算法導論原書。
推薦閱讀:Leo J. Guibas 和 Robert Sedgewick 於1978年寫的關於紅黑樹的一篇論文。
引言:
昨天下午畫紅黑樹畫了好幾個鐘頭,總共10頁紙。
特此,再深入剖析紅黑樹的算法實現,教你如何徹底實現紅黑樹算法。
經過我上一篇博文,“教你透徹了解紅黑樹”後,相信大家對紅黑樹已經有了一定的了解。
個人覺得,這個紅黑樹,還是比較容易懂的。
不論是插入、還是刪除,不論是左旋還是右旋,最終的目的只有一個:
即保持紅黑樹的5個性質,不得違背。
再次,重述下紅黑樹的五個性質:
一般的,紅黑樹,滿足一下性質,即只有滿足一下性質的樹,我們才稱之為紅黑樹:
1)每個結點要麼是紅的,要麼是黑的。
2)根結點是黑的。
3)每個葉結點,即空結點(NIL)是黑的。
4)如果一個結點是紅的,那麼它的倆個兒子都是黑的。
5)對每個結點,從該結點到其子孫結點的所有路徑上包含相同數目的黑結點。
抓住了紅黑樹的那5個性質,事情就好辦多了。
如,
1.紅黑紅黑,要麼是紅,要麼是黑;
2.根結點是黑;
3.每個葉結點是黑;
4.一個紅結點,它的倆個兒子必然都是黑的;
5.每一條路徑上,黑結點的數目等同。
五條性質,合起來,來句順口溜就是:(1)紅黑 (2)黑 (3)黑 (4&5)紅->黑 黑。
本文所有的文字,都是參照我昨下午畫的十張紙(即我拍的照片)與算法導論來寫的。
希望,你依照此文一點一點的往下看,看懂此文後,你對紅黑樹的算法了解程度,一定大增不少。
ok,現在咱們來具體深入剖析紅黑樹的算法,並教你逐步實現此算法。
此教程分為10個部分,每一個部分作為一個小節。且各小節與我給的十張照片一一對應。
一、左旋與右旋
先明確一點:為什麼要左旋?
因為紅黑樹插入或刪除結點後,樹的結構發生了變化,從而可能會破壞紅黑樹的性質。
為了維持插入、或刪除結點後的樹,仍然是一顆紅黑樹,所以有必要對樹的結構做部分調整,從而恢復紅黑樹的原本性質。
而為了恢復紅黑性質而作的動作包括:
結點顏色的改變(重新著色),和結點的調整。
這部分結點調整工作,改變指針結構,即是通過左旋或右旋而達到目的。
從而使插入、或刪除結點的樹重新成為一顆新的紅黑樹。
ok,請看下圖:

如上圖所示,‘找茬’
如果你看懂了上述倆幅圖有什麼區別時,你就知道什麼是“左旋”,“右旋”。
在此,著重分析左旋算法:
左旋,如圖所示(左->右),以x->y之間的鏈為“支軸”進行,
使y成為該新子樹的根,x成為y的左孩子,而y的左孩子則成為x的右孩子。
算法很簡單,還有注意一點,各個結點從左往右,不論是左旋前還是左旋後,結點大小都是從小到大。
左旋代碼實現,分三步(注意我給的注釋):
The pseudocode for LEFT-ROTATE assumes that right[x] ≠ nil[T] and that the roots parent is nil[T].
LEFT-ROTATE(T, x)
1 y ← right[x] ▹ Set y.
2 right[x] ← left[y] //開始變化,y的左孩子成為x的右孩子
3 if left[y] !=nil[T]
4 then p[left[y]] <- x
5 p[y] <- p[x] //y成為x的父母
6 if p[x] = nil[T]
7 then root[T] <- y
8 else if x = left[p[x]]
9 then left[p[x]] ← y
10 else right[p[x]] ← y
11 left[y] ← x //x成為y的左孩子(一月三日修正)
12 p[x] ← y
//注,此段左旋代碼,原書第一版英文版與第二版中文版,有所出入。
//個人覺得,第二版更精准。所以,此段代碼以第二版中文版為准。
左旋、右旋都是對稱的,且都是在O(1)時間內完成。因為旋轉時只有指針被改變,而結點中的所有域都保持不變。
最後,貼出昨下午關於此右旋算法所畫的圖:
左旋(第2張圖):

//此圖有點bug。第4行的注釋移到第11行。如上述代碼所示。(一月三日修正)
二、左旋的一個實例
不做過多介紹,看下副圖,一目了然。
LEFT-ROTATE(T, x)的操作過程(第3張圖):
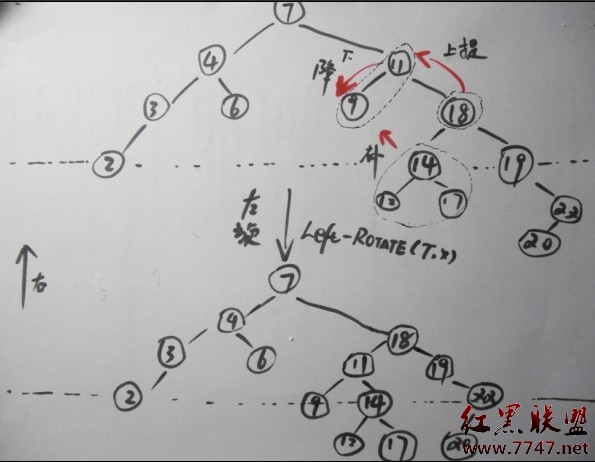
---------------------
提醒,看下文之前,請首先務必明確,區別以下倆種操作:
1.紅黑樹插入、刪除結點的操作
//如插入中,紅黑樹插入結點操作:RB-INSERT(T, z)。
2.紅黑樹已經插入、刪除結點之後,
為了保持紅黑樹原有的紅黑性質而做的恢復與保持紅黑性質的操作。
//如插入中,為了恢復和保持原有紅黑性質,所做的工作:RB-INSERT-FIXUP(T, z)。
ok,請繼續。
三、紅黑樹的插入算法實現
RB-INSERT(T, z) //注意我給的注釋...
1 y ← nil[T] // y 始終指向 x 的父結點。
2 x ← root[T] // x 指向當前樹的根結點,
3 while x ≠ nil[T]
4 do y ← x
5 if key[z] < key[x] //向左,向右..
6 then x ← left[x]
7 else x ← right[x] // 為了找到合適的插入點,x 探路跟蹤路徑,直到x成為NIL 為止。
8 p[z] ← y // y置為 插入結點z 的父結點。
9 if y = nil[T]
10 then root[T] ← z
11 else if key[z] < key[y]
12 then left[y] ← z
13 else right[y] ← z //此 8-13行,置z 相關的指針。
14 left[z] ← nil[T]
15 right[z] ← nil[T] //設為空,
16 color[z] ← RED //將新插入的結點z作為紅色
17 RB-INSERT-FIXUP(T, z) //因為將z著為紅色,可能會違反某一紅黑性質,
//所以需要調用RB-INSERT-FIXUP(T, z)來保持紅黑性質。
17 行的RB-INSERT-FIXUP(T, z) ,在下文會得到著重而具體的分析。
還記得,我開頭說的那句話麼,
是的,時刻