July 二零一一年一月
======================
本文主要參考:算法導論 第二版、維基百科。
寫的不好之處,還望見諒。
本經典算法研究系列文章,永久勘誤,永久更新、永久維護。
July、二零一一年二月十日更新。
一、Dijkstra 算法的介紹
Dijkstra 算法,又叫迪科斯徹算法(Dijkstra),
算法解決的是有向圖中單個源點到其他頂點的最短路徑問題。
舉例來說,
如果圖中的頂點表示城市,而邊上的權重表示著城市間開車行經的距離,
Dijkstra 算法可以用來找到兩個城市之間的最短路徑。
二、Dijkstra 的算法實現
Dijkstra 算法的輸入包含了一個有權重的有向圖 G,以及G中的一個來源頂點 S。
我們以 V 表示 G 中所有頂點的集合,以 E 表示G 中所有邊的集合。
(u, v) 表示從頂點 u 到 v 有路徑相連,而邊的權重則由權重函數 w: E → [0, ∞] 定義。
因此,w(u, v) 就是從頂點 u 到頂點 v 的非負花費值(cost),邊的花費可以想像成兩個頂點之間的距離。
任兩點間路徑的花費值,就是該路徑上所有邊的花費值總和。
已知有 V 中有頂點 s 及 t,Dijkstra 算法可以找到 s 到 t 的最低花費路徑(例如,最短路徑)。
這個算法也可以在一個圖中,找到從一個頂點 s 到任何其他頂點的最短路徑。
好,咱們來看下此算法的具體實現:
Dijkstra 算法的實現一(維基百科):
u := Extract_Min(Q) 在頂點集合 Q 中搜索有最小的 d[u] 值的頂點 u。這個頂點被從集合 Q 中刪除並返回給用戶。
1 function Dijkstra(G, w, s)
2 for each vertex v in V[G] // 初始化
3 d[v] := infinity
4 previous[v] := undefined
5 d[s] := 0
6 S := empty set
7 Q := set of all vertices
8 while Q is not an empty set // Dijkstra演算法主體
9 u := Extract_Min(Q)
10 S := S union {u}
11 for each edge (u,v) outgoing from u
12 if d[v] > d[u] + w(u,v) // 拓展邊(u,v)
13 d[v] := d[u] + w(u,v)
14 previous[v] := u
如果我們只對在 s 和 t 之間尋找一條最短路徑的話,我們可以在第9行添加條件如果滿足 u = t 的話終止程序。
現在我們可以通過迭代來回溯出 s 到 t 的最短路徑
1 s := empty sequence
2 u := t
3 while defined u
4 insert u to the beginning of S
5 u := previous[u]
現在序列 S 就是從 s 到 t 的最短路徑的頂點集.
Dijkstra 算法的實現二(算法導論):
DIJKSTRA(G, w, s)
1 INITIALIZE-SINGLE-SOURCE(G, s)
2 S ← Ø
3 Q ← V[G] //V*O(1)
4 while Q ≠ Ø
5 do u ← EXTRACT-MIN(Q) //EXTRACT-MIN,V*O(V),V*O(lgV)
6 S ← S ∪{u}
7 for each vertex v ∈ Adj[u]
8 do RELAX(u, v, w) //松弛技術,E*O(1),E*O(lgV)。
因為Dijkstra算法總是在V-S中選擇“最輕”或“最近”的頂點插入到集合S中,所以我們說它使用了貪心策略。
(貪心算法會在日後的博文中詳細闡述)。
===========================================
二零一一年二月九日更新:
此Dijkstra 算法的最初的時間復雜度為O(V*V+E),源點可達的話,O(V*lgV+E*lgV)=>O(E*lgV)
當是稀疏圖的情況時,E=V*V/lgV,算法的時間復雜度可為O(V^2)。
但我們知道,若是斐波那契堆實現優先隊列的話,算法時間復雜度,則為O(V*lgV + E)。
三、Dijkstra 算法的執行速度
我們可以用大O符號將Dijkstra 算法的運行時間表示為邊數 m 和頂點數 n 的函數。Dijkstra 算法最簡單的實現方法是用一個鏈表或者數組來存儲所有頂點的集合 Q,
所以搜索 Q 中最小元素的運算(Extract-Min(Q))只需要線性搜索 Q 中的所有元素。
這樣的話算法的運行時間是 O(E^2)。
對於邊數少於 E^2 的稀疏圖來說,我們可以用鄰接表來更有效的實現迪科斯徹算法。
同時需要將一個二叉堆或者斐波納契堆用作優先隊列來尋找最小的頂點(Extract-Min)。
當用到二叉堆時候,算法所需的時間為O(( V+E )logE),
斐波納契堆能稍微提高一些性能,讓算法運行時間達到O(V+ElogE)。(此處一月十六日修正。)
開放最短路徑優先(OSPF, Open Shortest Path First)算法是迪科斯徹算法在網絡路由中的一個具體實現。
與 Dijkstra 算法不同,Bellman-Ford算法可用於具有負數權值邊的圖,只要圖中不存在總花費為負值且從源點 s 可達的環路即可用此算法(如果有這樣的環路,則最短路徑不存在,因為沿環路循環多次即可無限制的降低總花費)。
與最短路徑問題相關最有名的一個問題是旅行商問題(Traveling salesman problem),此類問題要求找出恰好通過所有標點一次且最終回到原點的最短路徑。
然而該問題為NP-完全的;換言之,與最短路徑問題不同,旅行商問題不太可能具有多項式時間解法。
如果有已知信息可用來估計某一點到目標點的距離,則可改用A*搜尋算法,以減小最短路徑的搜索范圍。
=========================================
二零一一年二月九日更新:
BFS、DFS、Kruskal、Prim、Dijkstra算法時間復雜度的比較:
一般說來,我們知道,BFS,DFS算法的時間復雜度為O(V+E),
最小生成樹算法Kruskal、Prim算法的時間復雜度為O(E*lgV)。
而Prim算法若采用斐波那契堆實現的話,算法時間復雜度為O(E+V*lgV),當|V|<<|E|時,E+V*lgV是一個較大的改進。
//|V|<<|E|,=>O(E+V*lgV) << O(E*lgV),對吧。:D
Dijkstra 算法,斐波納契堆用作優先隊列時,算法時間復雜度為O(V*lgV + E)。
//看到了吧,與Prim算法采用斐波那契堆實現時,的算法時間復雜度是一樣的。
所以我們,說,BFS、Prime、Dijkstra 算法是有相似之處的,單從各算法的時間復雜度比較看,就可窺之一二。
四、圖文解析 Dijkstra 算法
ok,經過上文有點繁雜的信息,你還並不對此算法了如指掌,清晰透徹。
沒關系,咱們來幅圖,就好了。請允許我再對此算法的概念闡述下,
Dijkstra算法是典型最短路徑算法,用於計算一個節點到其他所有節點的最短路徑。
不過,針對的是非負值權邊。
主要特點是以起始點為中心向外層層擴展,直到擴展到終點為止。
[Dijkstra算法能得出最短路徑的最優解,但由於它遍歷計算的節點很多,所以效率低。]
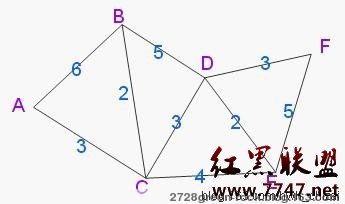
ok,請看下圖:
如下圖,設A為源點,求A到其他各所有一一頂點(B、C、D、E、F)的最短路徑。線上所標注為相鄰線段之間的距離,即權值。
(注:此圖為隨意所畫,其相鄰頂點間的距離與圖中的目視長度不能一一對等)
Dijkstra無向圖
算法執行步驟如下表: